D'Arcy Thompson on Greek irrationals
D'Arcy Thompson published Excess and Defect; or the little more and the little less in Mind 38 (149) (1928). We give here a version of the article. The original contains some Greek quotes. As part of the purpose of the article is to discuss the translation of these pieces of Greek text, this give some difficulty in presenting the article for readers who do not know any Greek. However, we have attempted to make it as understandable as possible while trying to keep the style of the original article. Where we have replaced a Greek word, a Greek phrase, or a Greek passage by a translation, we enclose the material in square brackets and [colour it red].
EXCESS AND DEFECT: OR THE LITTLE MORE AND THE LITTLE LESS
In two recent papers, Prof A E Taylor has discussed the Platonic or Pythagorean philosophy of Number, as Plato and Aristotle relate it to us and as it may be further elucidated in various ways. In particular he compares the account of the irrational numbers given in the Epinomis with the descriptions (well-known to students of Greek mathematics) which Theon, lamblichus and Proclus give of the so-called 'side and diagonal numbers'; and he shows that, somehow or other, these side and diagonal numbers are connected with what Plato means by the 'One and the Great-and-small' as constituents of Number.
Aristotle gives us the following statement of Plato's concept of the 'genesis of number': [Number is derived from Unity and the indeterminate dyad]; but this apparently simple statement has never been satisfactorily explained. Though we do our best to collate it with other related passages we are left in doubt in the end; there is confusion or contradiction somewhere which no man has found his way through, and I begin to think that our first business is to inquire what is meant by 'number' in this particular connexion. Aristotle's statement might refer, and it is usually supposed to refer, to the genesis of Number in its widest sense, to the genesis of the ordinary numbers 1, 2, 3 . . . from One and from one another: a question which is either simplicity itself or a transcendental problem of extreme subtlety.
This particular process of generation has never been shown to be related to the so-called [infinite/indeterminate dyad]. On the other hand, [the number] may be used here in its technical sense, meaning a surd or 'irrational number', especially √2; and the general problem of Number may never have been in question at all. It was the irrational number, the numerical ratio (if any) between two incommensurable segments, which was a constant object of search, whose nature as a number was continually in question, and whose genesis as a number cried aloud for explanation or justification. I am inclined to think that this restricted but vitally important problem is the question at issue; but if it be only part of a more general question, it is still the only part thereof which seems capable of explanation. In short if we keep to this restricted definition of our problem, and if we then go a step or two farther in its interpretation than Prof Taylor has gone, we come to a very simple understanding of what [the one/unity] and the [infinite/indeterminate dyad] are; and of how, between them both, such a 'number' as √2 is generated.
The 'side and diagonal numbers', as Theon and Iamblichus explain them, hark back to the all-important Theorem of Pythagoras, and to the simplest case thereof where the right-angled triangle is also isosceles. By their means we 'arithmeticize' this construction, and for certain values of the side obtain 'rational values' for the corresponding diagonal; consequently, dividing the diagonal-number by the side-number, we obtain an approximation to, or a 'rational value' for, √2, the true ratio of diagonal to side. It is part of the great Pythagorean principle of letting mathematics rest on an arithmetical basis. It is just worth mentioning that what we here call the diagonal is called in Greek the diameter; it is the diagonal of the completed square (or parallelogram), and the diameter of the circle in which it can be described.
The following is a table of the side and diagonal numbers ([side and diagonal numbers] (literally [number of units in the sides and diagonals])) - Proclus (28, 10) gives the series as far as 12, 17, and adds - [and always thus (etc.)].
| Sides
([sides]) 1 2 5 12 29 70 169 etc. | Diagonals
([diagonals]) 1 3 7 17 41 99 239 |
, etc.
Theon puts it in yet another way; for he tells us that a diagonal must be added to a side [to get the next side], and two sides to a diagonal [to get the next diagonal] - 'for what side does by two steps ( literally [it is worth two]) that diagonal does by one'. He is thinking, as Hultsch has told us, of Euclid II. 10.
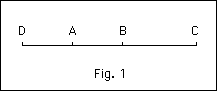
For, in the line , if and be as side and diagonal, then .
Further, if , then (II. 10)
.
Therefore ; therefore are as side and diagonal. But is the old side plus the old diagonal; and is the old diagonal plus two sides.
The table of side and diagonal numbers has many other properties. For instance, as Proclus tells us, the sum of the squares of two adjacent diagonals = twice the sum of the squares on the two corresponding sides: e.g. 32 +72 = 2(22 + 52 ). And, in Chapter xxiii he shows, following Adrastus, that the sum of the squares of 'all' the diagonals is equal to twice the sum of the squares of 'all' the sides.
As Prof Taylor explains, this table is precisely equivalent to what, in our arithmetic, we call a continued fraction, viz.,
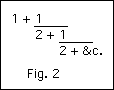
But while we may illustrate our problem in this way, I do not think we simplify it. The continued fraction is an elegant arithmetical device, and the mathematician calls it a simplified expression; but it does not follow that it is simple to work with. Carry it on to ten or twenty terms, and it becomes a troublesome matter to evaluate; while the Greek side-and-diagonal numbers may be carried as far as you please, and still require only the easiest arithmetic.
The Greek table has another advantage over our continued fraction, in that it obviously is just what it purports to be, namely an arithmetization of the corresponding geometrical figure. We have merely to take twice the square of a side-number to get, approximately, the square of the opposite diagonal number: and when we proceed to do so systematically we discover three curious and important things. Firstly, the successive results are closer and closer approximations to that irrational number (viz., √2) which is the 'limit', the unattainable limit, of the series. Secondly, the approximations are alternately on one side or the other, a little more or a little less than the number at which we aim; and herein lies the technical meaning in Greek arithmetic of 'excess and defect', (literally [a falling short and an exceeding]). Thirdly, the striking and beautiful fact appears that this 'excess or defect' is always (in this case) capable of being expressed by a difference of 1. The square of the diagonal number (i.e. of what Socrates calls the 'rational diagonal') is alternately less or more by one than the sum of the squares of the sides:
2 × 12 = 12 + 1
2 × 22 = 32 - 1
2 × 52 = 72 + 1
2 × 122 = 172 - 1
etc.
This property of the side- and- diagonal series, that not merely is the square of the one in alternate excess and defect as compared with twice the square on the other, but that this alternate excess and defect is in every case measured by one unit, is expressly stated by Theon and by Proclus. The [rational diagonal] (literally [the diagonal that can be spoken]) is explained as being made less or more than that from the side by one (28, 14) ; or again, on the same page, [Let there be shown arithmetically on the rational diagonal, as we said, greater or less by one. Let there be a unity, around which there is another unity making a dyad, etc.]
2 × 22 = 32 - 1
2 × 52 = 72 + 1
2 × 122 = 172 - 1
etc.
[One], in short, is the word used both for that unit with which the series on either side begins, and for that unit which is at every successive stage the measure of excess or defect. For Unity comes into the case in a twofold capacity. It is the beginning, the [start] of the whole series , then again, as the series proceeds, the 'One' has to be imported into each succeeding Dyad, where it defines ([defines]) the amount of excess or defect, and equates or equalizes ([equals]) the two incompatible quantities.
Now the question arises whether this [monad] be not identical with the [one], which in Plato's language is said to combine with the 'Great-and-Small' in constructing for us the real number. That the side and diagonal numbers show us what Plato means by the Great-and-small, or Aristotle by his Excess-and-defect, is certain; Prof Taylor has made it seem clear and even obvious, but he has not by any means made it clear what Plato meant by [one]. It seems to be in his mind that [one] is that infinitely far-off Limit, where the two sides of the Dyad merge into one, and where the great and small no longer differ. I believe it has a much simpler and more prosaic meaning; and that it is merely another name for that unit or 'monad' which we continually subtract from the 'great' or add to the 'small', and which so constructs for us the real number. This point, this precise nature of the agency of the 'One', and the simple explanation which it involves of the precise meaning of [to define] or [to equal], both seem to me to be made clear by our study of the Greek side-and-diagonal series; but the point is lost as soon as we replace that formula by the continued fractions of our modern arithmetic. Prof Taylor, so it seems to me, has treated the successive convergents of the continued fraction as identical with the successive fractions of the Greek series. So they are, in the end. As he says, 'they never actually meet, since none of the "convergents" is ever the same as its successor, but by proceeding far enough with the series we can make the interval between two successive "convergents" less than any assigned difference, however small.' Precisely so; but all the while that 'monad' in which the excess or defect consists is never seen in the convergents of the continued fraction; and indeed it is so effectually concealed that Prof Taylor neither recognizes its importance nor even mentions it at all.
Similar tables can be constructed, as the Greeks well knew, for other square roots; and the way to construct them is in each case easy to discover. For instance, the table for is as follows:
| 1 2
4 9 17 38 72 161 etc. | According to which table | 5 × 12 = 22 + 1
5 × 42 = 92 - 1 5 × 172 = 382 + 1 5 × 722 = 1612 - 1 etc. |
| 1 4
8 33 65 etc. | Hence | 17 × 12 = 42 + 1
17 × 82 = 332 - 1 etc. |
The case of √3 is a somewhat remarkable one. It may be represented in our arithmetic by the continued fraction
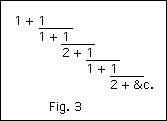
identical with the series of convergent fractions beginning 1 /1 , 2 /1 , 5 /3 etc., which we may set forth as follows, in tabular form:
1 2 3 5 4 7 11 19 15 26 41 71 56 97 153 256 209 362 571 989 780 1351 etc. | Applying this table as before, we find that | 3 × 12 = 22 - 1
3 × 32 = 52 + 2 3 × 42 = 72 - 1 3 × 112 = 192 + 2 etc. |
We have set forth this table at greater length than the others because it so happens that Archimedes makes use of certain of its higher convergents. He tells us, without further explanation, that √3 lies between 1351 /780 and 265 /153 , being less than the former and greater than the latter. This statement is quite correct; for the former fraction squared gives the value 3.000017 .... the latter gives 2.999936....
It is strange, however, that Archimedes should apparently skip over two convergents in making his comparison; he might have narrowed the issue by telling us that √3 was greater than 989 /571 . But he used an abbreviated table, which he had probably constructed in a somewhat different way. For we may begin, as the table begins, by taking √3 as being nearly equal to 5/3; therefore 3√3 - 5 is small. Now
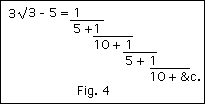
which continued fraction is identical with the series of convergent fractions 1 /5 , 10 /51 , etc. Whence we find the convergents to √3 to be 5 /3 , 26 /15 , 265 /153 , 1351 /780 , etc.; in short, we have the very series from which Archimedes may have drawn his examples, without omissions. Archimedes may have done it in this way; there is nothing we need put beyond his powers. But I feel pretty sure that all these tables were originally arrived at in a much simpler and more plodding way, by trial and error. An old arithmetician may have searched (as we might search through Barlow's Tables) for a square number which was the double of some other square; he would fail to find one. But he would very soon find that 32 was nearly the double of 22 ; searching for another such case, he would find that 72 was nearly the double of 52 ; and by the time he had found a third instance he would be on the brink of the rule which connects them all, and defines the series.
We have now seen that in the convergent series leading to √3, the 'One' is no longer the unique and indispensable 'equalizer'; and we shall soon see that it is by no means indispensable (though at first it seemed so) in the series of side and diagonal numbers which leads to √2. For the ordinary two-column table of side and diagonal numbers, as Theon describes it and with which we began, may be extended as follows:
±1/4 ±1/2 ±1 ±2 ±4 ±8 ±16
-------------------------------------------
1/2 1/2 1 1 2 2 4 4
1 3/2 2 3 4 6 8 12
5/2 7/2 5 7 10 14 20 28
6 17/2 12 17 24 34 48 68
29/2 41/2 29 41 58 82 116 164
etc.
In this extended table each column may serve by turns for side-numbers or for diagonals; and the 'equalizing factor', the amount of excess or defect, which began with ±1, becomes in the next column ±2, then ±4, ±8 and so on. The table may also be extended towards the left-hand side, where the first extended column will show an equalizing factor of ±1/2, and so on. All this arithmetic is so simple that it can hardly have escaped the notice of any calculator who pondered over the elementary table with which we began. To proceed from our first table for the values of √2 to those giving values for √3, √5, etc. (as we have seen that the Greeks did), was neither an easier nor a harder operation than to pass from that same table where the values of √2 are 'equalized' by 1, to the extended table where they are 'equalized' by 2, or powers of 2. But such an extension of the table of side and diagonal numbers is neither mentioned nor described. It may have escaped notice, though this is unlikely. It may have seemed of little importance, though this seems unlikelier still. It may have been one of those things of which the less said the better; for, if my interpretation be correct of what was meant by the One as the continual 'equalizer' of the never-ending Dyad, the whole theory would receive a shock on the revelation that, mutatis mutandis, the same part could be played by 2 or by 4.
There is still another table which may be just as easily or indeed still more easily derived from the first, and which is of very great importance. Yet there is no account of it, nor the least allusion to it, in all the history of Greek mathematics; and it is commonly believed to have been first made known by the great arithmetician who introduced the Arabic numerals into the Christian world.
We remember that, to form our table of side and diagonal numbers, we added each side-number to its own predecessor, that is to say, to the number standing immediately over it in the table, and so we obtained the next diagonal; thus we add 5 to 2 to get 7, in the following:
1 1 2 3 5 7 12 etc.
1 1 2 3 5 8 13 21 34 55 etc.
1, 1, 2, 3, 5, 8, 13, 21, etc.
It is identical with the simplest of all continued fractions,
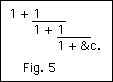
Its successive pairs of numbers, or fractions, as 5/3, 8/5, etc., are familiar to botanists, ever since Bravais showed them to express the number of spirals which may be counted, to right and to left, on a fir-cone or any other complicated inflorescence.
Here is another of the many curious properties of the series:
02 + 22 = 2(12 + 12 )
12 + 32 = 2(12 + 22 )
12 + 52 = 2(22 + 32 )
22 + 82 = 2(32 + 52 )
etc.
But the main property, the essential characteristic, of these pairs of numbers, or fractions, is that they approximate rapidly, and by alternate excess and defect, to the value of the Golden Mean, that is to say to the value of
(√5 - 1)/2 = 0.618... Thus the successive fractions 1 /2 , 2 /3 , 3 /5 , , etc., expressed in decimals, are as follows:
0.5, 0.66... , 0.6, 0.6153... , 0.6190... , 0.6176... , 0.6181... , etc.
The Golden Mean itself is only the numerical equivalent, the 'arithmetization', of Euclid II. 11 ; where we are shown how to divide a line in 'extreme and mean ratio', as a preliminary to the construction of a regular pentagon: that again being the half-way house to the final triumph, perhaps the ultimate aim, of Euclidian or Pythagorean geometry, the construction of the regular dodecahedron, Plato's symbol of the Cosmos itself. Euclid himself is giving us a sort of algebraic geometry, or rather perhaps a geometrical algebra; and the series we are now speaking of arithmeticizes that geometry and that algebra. It is surely much more than a coincidence that this series is closely related to Euclid II. 11, and the other (as Theon expressed it) to the immediately preceding proposition.
In the line (AC) divided in extreme and mean ratio we have three magnitudes, AC, AB, BC, such that BC2 = AB. AC [there is a misprint here in the original article that we have corrected].
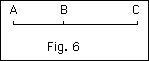
And in our table, any three consecutive numbers may represent these three geometrical magnitudes, the square of the intermediate number being equivalent - approximately equivalent - to the product of the other two. Observe that precisely as in the former case the approximation gets closer and closer; there is alternate excess and defect, and (above all) the 'One' is needed in every case, to equate the terms or remedy the defective approximation; e.g.
52 = 3 × 8 + 1
82 = 5 × 13 - 1
132 = 8 × 21 + 1
etc.
Our two series started alike, with 1 and 1 - the [beginning] of all arithmetic. We added 1 to 1, then 2 to 1, and got
1 . 1
2 . 3
But in the one case we added our 2 to the left-hand 1, and in the other to the right-hand; and the difference shows itself in the next line:
1 . 1 or 1 . 1
2 . 3 2 . 3
5 . 7 5 . 8
12 . . 13 . .
Of the two series which thus begin alike and then part company, the one leads to the square-root of 2 or the hypotenuse of an isosceles right-angled triangle, and the other leads to the Divine or Golden Section. These are the two famous surds or 'irrational numbers' of antiquity, and they are also the two pillars of Euclidian geometry.
It is inconceivable that the Greeks should have been familiarly acquainted with the one and yet unacquainted with the other of these two series, so simple, so interesting and so important, so similar in their properties and so closely connected with one another. Between them they arithmeticize what is admittedly the greatest theorem, and what is probably the most important construction, in all Greek geometry. Both of them hark back to themes which were the chief topics of discussion among Pythagorean mathematicians from the days of the Master himself; and both alike are based on the arithmetic of fractions, with which the early Egyptian mathematicians and doubtless the Greek also were especially familiar. Depend upon it, the series which has its limit in the Golden Mean was just as familiar to them as that other series whose limit is √2.
The Golden Mean series is a very curious one; and we have put it only in one and that the simplest of its many forms. For the fact is, we may begin it as we please, with 1, 1, or 1, 2, or 1, 3, or any two numbers whatsoever, whole or fractional, and in the end it comes always to the same thing! For instance, we may have the series
1, 5, 6, 11, 17, 28, 45, 73, 118, 191, 309, etc.,
which only agrees with the former in that each number is the sum of its two predecessors: but as before, the fractions soon approximate closely to the Golden Mean; 191/309 = 0.61812 . . . ; and (as a consequence) 309/191 = 1.618 ... approximately.
These two methods, of finding the value of √2 and the value of the Golden Mean, are, be it remarked, by no means mere rough approximations, but they actually lead, more easily and quicker than does our modern arithmetic, to results of extreme accuracy. In the case of the side and diagonal numbers we need go no farther than the tenth place in the table (as can be done in less than two minutes) to get a fraction which is equivalent to the value of √2 to six places of decimals!
Remembering the immense interest which the ancients took in the decagon, the pentagon and their related solids, let us see how our side-and-diagonal table and the closely related table of the Golden Mean may help us in studying these. We know (from Euclid IV. 10) that the side of the decagon is equal (in terms of the radius) to the Golden Mean = (√5 - 1)/2 = 0.618 ... ; let τ be this Golden Mean - [section (literally a cut)], the Section, as the Greeks called it. We also know that the side of the star-decagon = (√5 + 1)/2 = 1 + τ. The side of the decagon, then, or the star-decagon, may be read off at once to any required degree of accuracy from our table of the Sectio Divina or Golden Mean, or in other words from our Fibonacci series. The side of the pentagon is
√((5 - √5)/2) = √(1 - τ2 ) = √(2 - τ).
Selecting any convenient fraction from the same table, for instance 89/144 we may then define the length of the side of the inscribed pentagon (still in terms of the radius) as
√(2 - 89/144) = √199/12 = (nearly) √2 × 5/6.
Again choosing, from the other table, a fraction approximately equal to √2, we have (for instance) 99/70 × 5/6 = 1.178..., which is a correct value for the side of the pentagon to its three places of decimals.
The squares on the sides of the regular decagon and pentagon and on the corresponding, star-polygons are still more easily dealt with; for (calling and the side of the decagon and star-decagon respectively) we have
And we may read every one of these off, as accurately as we please, from our Fibonacci numbers.
All this is a beautifully simple illustration of a principle recognized in modern mathematics, that you may immensely extend the efficiency (so to speak) of the series of natural numbers if only you can add one other number to it. 1, 2, 3.... carry us a long way; but if we add to this consecutive series either √2, or π, or the number we have now called τ, in each case an immense new field of operations is rendered possible. π presents some difficulties of its own; but the determination of √2 or of τ to any required degree of accuracy should have presented no difficulty even to very early and primitive arithmeticians.
The cube root of 2 is another story. We can neither represent it by a continued fraction nor by a series of side-and-diagonal numbers. I feel pretty sure that the peculiar importance and air of mystery attaching to the Delian Problem arose simply from the fact that for the extraction of a cube root you have no such arithmetical device as that by which a square root can be extracted so easily and so accurately.
The technical phrase 'excess or defect' is sometimes used, especially by Aristotle, in a sense which is obviously not the arithmetical one, though it must be more or less analogous thereto. A single instance must suffice. In the first chapter of the Historia Animalium, Aristotle tells us that, within the limits of a 'genus', such as Bird or Fish, the difference between one form or species and another is of the nature of 'excess or defect'; that their corresponding parts differ in property or accident, or in the degree to which they are subject to this or that property or accident, or in number or in magnitude - in short always, after some fashion or other, in the way of excess or defect. When I translated the Historia Animalium many years ago, I took this statement to be neither more nor less than a foreshadowing of our own comparative morphology. I supposed that Aristotle would regard each species of bird much as a modern morphologist does; that he would recognize the correspondence or homology of their several parts; and that he saw, better perhaps than many morphologists do, how the differences between these corresponding parts are essentially quantitative differences, or 'differences of degree'. The chief difference between Aristotle's point of view and ours seemed merely to be that he limited his comparison, or his concept of homology, to the species of a single 'genus'; whereas the evolutionary morphologist seeks (not always with success), to trace detailed homologies between one Aristotelian genus and another.
But now that we understand the phrase excess-and-defect better than ever before, we may read its technical meaning into the Aristotelian passage and find the whole significance vastly altered and improved. For I take it now that Aristotle was thinking, more Platonico, of all the fowls of the air as mere visible forms or [shapes], mere imperfect representations of, or approximations to, their prototype the ideal Bird. Just as we study the rational forms of an irrational number and through their narrowing vista draw nearer and nearer to the ideal thing, but always fail to reach it by the little more or the little less: so we may, as it were, survey the whole motley troop of feathered things only to find each one of them falling short of perfection, deficient here, redundant there: all with their inevitable earthly faults and flaws. Then beyond them all we begin to see dimly a bird such as never was on sea or land, without blemish, whether of excess or defect: it is the ideal Bird, the [model which is set in heaven].
Last Updated April 2007