Edmund Taylor Whittaker wrote the article Mathematics and Logic which was published in James R Newman (ed.), What is Science? (Simon and Schuster, 1955), 20-62.
We must, of course, look at Whittaker's article as part of the history of the "history of mathematics." In the 70 years since the article was written much more has been understood about the beginnings of mathematics and very much more about astronomy and the universe. But this does not reduce the value of the article, rather it helps us to understand how the history of mathematics develops.
We must, of course, look at Whittaker's article as part of the history of the "history of mathematics." In the 70 years since the article was written much more has been understood about the beginnings of mathematics and very much more about astronomy and the universe. But this does not reduce the value of the article, rather it helps us to understand how the history of mathematics develops.
Mathematics and Logic by E T Whittaker
The First Mathematicians
Mathematics is in this book regarded as a kind of science. But there is a great difference between mathematics and the other recognised branches of science, as can be seen when we examine the nature of a typical mathematical theorem. Take for instance this, which was originally enunciated in the eighteenth century by Edward Waring of Cambridge: "Every positive whole number can be represented as the sum of at most nine cubes." With Waring this was really no more than a guess based on observation of a great number of particular cases; but evidently mere observation cannot furnish a proof that the theorem is true in general, and indeed a strict proof of this theorem was not known until more than a century later. Let us see how the notion of a science that depends on logical proof came into being.
Historians are generally agreed that this development originated with the Greek philosophers of the sixth and fifth centuries before Christ. To be sure, the arts of calculation and measurement had made considerable progress before this, amongst the ancient Babylonians and Egyptians, who were able to solve numerical problems beyond the powers of most modern schoolboys; but the procedure which is characteristic of mathematics as we know it, the proving of theorems, was introduced by the Greeks.
The records are scanty, and generally later in date by some centuries than the events referred to. But there can be no doubt that the movement began in the fringe of Greek settlements along the coast of Asia Minor, which were in contact with the older civilisations of the East, and were at the time enjoying peace and prosperity. The new principle that was central in their philosophy was the conviction that the world has a unity; in a polytheistic society they were essentially monotheists, and they held that science is of one pattern. The first of them whose name has come down to us, Thales of Miletus (640?-546 B.C.) taught that all matter is essentially one, that it consists, in fact, of modifications of water. His successor, Anaximander, the second head of the school, opened wider possibilities by asserting only that there is one primitive formless substance everywhere present, out of which all things were made.
Thales is credited with the discovery of the mathematical theorem that "the angle in a semicircle is a right angle." This differs in character from the geometrical facts known to the ancient Egyptians, which had been concerned with areas. Thales seems to have been the first thinker to make lines and curves (which are abstractions) fundamental. For him, the theorem was probably a simple fact of observation. He would be familiar with wall decorations in which rectangles were inscribed in circles: a diagonal of a rectangle is also a diagonal of the corresponding circle, and the right angle formed by two sides of the rectangle is therefore the angle standing on a diameter, i.e., it is the angle in a semicircle.
The Place of Logic in Geometry
The disciples of Thales based their doctrine of physics on the assumption of a single ever-present medium which could undergo modifications. So far as the relations of physical objects with each other were concerned, they knew little beyond the experimental arts of surveying and measuring which they had inherited from the Egyptians and Babylonians. The Greeks of the next generation, however, developed this primitive geometry into an independent science, in which the whole corpus of the properties of figures in space, such as the theorem that the angle in a semicircle is a right angle, were deduced logically from a limited number of principles which were regarded as obviously true and so could be assumed: such as that if equals are added to equals, the sums are equal and the whole is greater than its parts. These principles were given the name of common notions (koinai ennoiai), and later of axioms (axiomata).
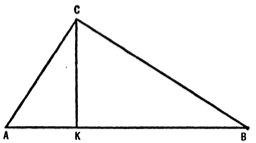
This rational geometry was discovered not by the philosophers of Asia Minor (who disappear from history not long after the fall of Miletus in 494 B.C., but by another school which sprang up in the Greek settlements in southern Italy, and which took the name of Pythagoreans from its founder Pythagoras (582?-aft. 507 B.C.). The famous theorem, that in a right-angled triangle the sum of the squares of the sides containing the right angle is equal to the square of the hypotenuse, is called by his name, probably with justice, though the Babylonians had methods of finding the length of the hypotenuse which doubtfully suggest some knowledge of it. It may seem strange that a proposition whose proof (as given in modern textbooks) is comparatively difficult, should have become known at such an early stage in the history of the subject; but it must be explained that the Pythagoreans had inherited from the pyramid-builders of Egypt the notion of similarity in figures, and that Pythagoras' theorem can be proved very easily when this notion is used. Thus, if is a triangle right-angled at , and is perpendicular to , then the triangle is the sum of the triangles and . But these are three similar triangles, and their areas are proportional to the areas of any other figures erected on the corresponding sides, which are similar to each other, in particular to the squares on these sides: whence immediately we have .
The new field of rational geometry was recognised as one in which progress was possible indefinitely; and practically the whole of the geometry now studied in schools was discovered by the Pythagoreans between 550 B.C. and 400 B.C.
To Thales' principle, that different kinds of matter are portions of a primitive universal matter, Pythagoras adjoined another principle, namely that the differences between different kinds of matter are due to differences in geometrical structure, or form. Thus the smallest constituent elements of fire, earth, air, and water, were respectively a tetrahedron, a cube, an octahedron, and an icosahedron. This belief led to much investigation on the theory of the regular solid bodies, which is the underlying subject of the great work in which the Pythagorean geometry was eventually set forth, the Elements of Euclid.
The Discovery of Irrationals
The Pythagoreans held that the principles of unity, in terms of which the cosmos was explicable, were ultimately expressible by means of numbers; and they attempted to treat geometry numerically, by regarding a geometrical point as analogous to the unit of number - a unit which has position, as they put it. A point differs from the unit of number only in the additional characteristic that it has location; a line twice as long as another line was supposed to be formed of twice as many points. Thus space was regarded as composed of separate indivisible points, and time of separate instants; for when the Greeks spoke of number, they always meant whole number. A prospect was now opened up of understanding all nature under the aspect of countable quantity. This view was confirmed by a striking discovery made by Pythagoras himself, namely that if a musical note is produced by the vibration of a stretched string, then by halving the length of the string we obtain a note which is an octave above the first note, and by reducing the length to two-thirds of its original value we obtain a note which is at an interval of a fifth above it. Thus structure, expressible by numerical relations, came to be regarded as the fundamental principle of the universe.
In carrying out the program based on this idea, however, the Pythagoreans came upon difficulties. For instance, they asked, what is the ratio of the number of points in the side of a square to the number of points in the diagonal? Let this ratio be where and are whole numbers having no common factor. Then since the square of the diagonal is, by Pythagoras' theorem, twice the square of the side, we have . From this equation it follows that is an even number, say , where is a whole number. Therefore , so m also is even, and therefore and have a common factor, contrary to hypothesis. Hence the ratio of the number of points in the side of a square to the number of points in the diagonal cannot be expressed as a ratio of whole numbers: we have made the discovery of irrational numbers. Since ratios such as this could exist in geometry but could not exist in the arithmetic of whole numbers, the Pythagoreans concluded that continuous magnitude cannot be composed of units of the same character as itself, or in other words, that geometry is a more general science than arithmetic.
The Paradoxes of Zeno
The logical difficulty created by the discovery of irrationals was soon supplemented by others, which the Greek philosophers of the fifth century BC constructed in their attempts to understand some of the fundamental notions of mathematics.
Let a ball be bouncing on a floor, and suppose that whenever it hits the floor it bounces back again, and remains in the air for half as long a time as on the preceding bounce. Will it ever stop bouncing?
If the duration of the first bounce is taken as 1, then the durations of the succeeding bounces are etc., and the sum of these durations is . Now let these durations be represented on a line: if is the middle point of a line and if is the middle point of , the middle point of the middle point of , and so on, then if ,
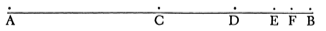
we have , etc., and the whole length AB is
.
But the whole length is 2. So after a time 2, the bouncing will have stopped, a fact which is perhaps at first sight difficult to understand when we reflect that whenever the ball comes down, it goes up again.
A famous paradox, due to Zeno (490?-435 B.C.) is that of the race between Achilles and the tortoise. The tortoise runs (say) one-tenth as fast as Achilles, but has a start of (say) 100 yards. By the time Achilles has run this 100 yards and is at the place the tortoise started from, the tortoise is 10 yards ahead: when Achilles has covered this 10 yards, the tortoise is 1 yard ahead: and so on forever - Achilles never catches up. This conclusion is obviously contrary to common sense. But we may remark that if Achilles is required to ring a bell every time he reaches the spot last occupied by the tortoise, then there will be an infinite number of such occasions, and the time required for the overtaking will indeed be infinite. The point is, that a finite stretch of space can be divided into an infinite number of intervals, and if those intervals are noted in review one by one, then the time required for the review is infinite.
The Beginnings of Solid Geometry in the Atomistic School
About the end of the fifth century B.C., some philosophers, of whom the most celebrated was a Thracian named Democritus, accepted the existence of empty space (which had been denied by the school to which Zeno belonged) and taught that the physical world is composed of an infinite number of small hard indivisible bodies (the atoms) which move in the void. All sensible bodies are composed of groupings of atoms. This notion was applied in order to calculate the volume of a cone or pyramid. The pyramid was conceived as a pile of shot, arranged in layers parallel to the base, the quantity of shot in any layer being proportional to the area of the layer and so to the square of the distance of the layer from the vertex of the pyramid. Then by summing the layers, it was found that the volume of the cone or pyramid is one-third the volume of a prism of the same height and base.
The Parallel Axiom
When the Greek philosophers based mathematics on axioms, they believed axioms to be true statements, whose truth was so obvious that they could be accepted without proof. One of the axioms they used, however, was felt to be not perfectly obvious, and for over twenty centuries attempts were made to prove it, by deducing it from other axioms which could be more readily admitted. This parallel axiom, as it is called, was stated by Euclid thus: if a straight line falling on two straight lines makes the interior angles on the same side less than two right angles, the two straight lines, if produced indefinitely, meet on that side on which are the angles less than two right angles.
Euclid himself seems to have had some hesitation about it, for he avoided using it in his first 28 propositions. He wished, however, to study parallel lines (that is, lines which are in the same plane, and, being produced ever so far both ways, do not meet), and he found that a theory of parallel lines could not be constructed without this axiom or something equivalent to it.
The Greeks, although they did not really doubt the truth of the parallel axiom, constructed arguments which seemed to disprove it. Thus, let be a straight line falling on two straight lines, and making the interior angles on the same side , together less than two right angles. On take and on take .
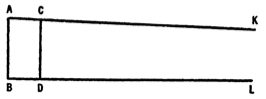
Then the lines, cannot meet within the ranges , since if they did, two sides of a triangle would be less than the third side. We now have the line falling on the two straight lines , and making the interior angles on the same side less than two right angles, so we can repeat the argument. By repeating it indefinitely often, we can conclude that the two lines , will never meet. The fallacy in the argument is of course the same as in the paradox of Achilles and the tortoise. Namely, the distance from to the meeting-point is by this process divided into an infinite number of segments; if we consider the operation of forming these segments one by one in turn, we shall never come to the end of the process.
Many axioms have been proposed at different times as substitutes for the parallel axiom, capable of leading logically to the theory of parallels; one such axiom consists in affirming the existence of triangles similar to each other, but of different sizes; and another axiom consists in the statement that two straight lines which intersect one another cannot both be parallel to the same straight line. Either of these two substitutes seems to be more obviously true than Euclid's parallel axiom; but early in the eighteenth century an Italian Jesuit named Saccheri (1667-1733) thought of what seemed a still better plan, namely to prove Euclid's original parallel axiom by showing that a denial of its truth leads to a reductio ad absurdum. He carried out this program and showed that when the parallel axiom is not assumed, a logical system of geometry can be obtained, which however differs in many respects from the geometry universally believed to be true: for instance, the sum of the angles of a triangle is not equal to two right angles. Saccheri considered that by arriving at this result he had achieved his aim of obtaining a reductio ad absurdum and thereby had shown that the parallel axiom is true. He never for one moment imagined that the system he had found could be proposed as an alternative to Euclidean geometry for the description of actual space.
The Geometry of Astronomical Space
In the nineteenth century however, some doubts were expressed as to whether the properties of space were represented everywhere and at all times by the geometry of Euclid. "The geometer of today," wrote W K Clifford (1845-1879), "knows nothing about the nature of the actually existing space at an infinite distance: he knows nothing about the properties of the present space in a past or future eternity."
Let us look into this question by considering a triangle in astronomical space, having its vertices, say, at the sun and two of the most distant nebulae, and having as its sides the paths of light-rays between these vertices. Then at each of the three vertices there will be an angle between the two sides that meet there. Have we any reason to believe that the sum of these three angles at the vertices will be equal to two right angles? Obviously it is not practicable to submit the matter to the test of observation; and we can find no logical reason for believing that the sum must necessarily be two right angles, since Saccheri's work showed that Euclidean geometry is not a logical necessity. Euclidean geometry is certainly valid, to a very close degree of approximation, for the triangles that we can observe in the limited space of a terrestrial laboratory. In their case its departure from truth is imperceptible, but for much larger triangles we must admit that neither logic nor observation gives us any decision.
We must therefore regard it as possible that in the astronomical triangle the sum of the three angles may be different from two right angles. We must recognise that empty space may have properties affecting measurements of size, distance, and the like: in astronomical space the geometry is possibly not Euclidean.
A language has been invented by mathematicians to describe this state of affairs. We know that the geometry of figures drawn on a curved surface, for instance the surface of a sphere, is different from the geometry of figures drawn in a plane, which is Euclidean; and this suggests a way of speaking about a three-dimensional space in which the geometry of solid bodies is not Euclidean: we say that in such a case, the space is curved. Astronomical space, then, may have a small curvature. This has long been recognised as a possibility, but it was not until the present century that the idea was developed into a definite quantitative theory. In 1929 the American astronomer E P Hubble announced as an observational fact that the spectral lines of the most distant nebulae are displaced toward the red end of the spectrum, by amounts which are proportional to the distance of the nebulae. This red-displacement was interpreted to mean that the nebulae were receding from us with velocities proportional to their distances; in fact, that the whole universe was expanding, all distances continually increasing proportionally to their magnitudes. Combining this with the results of theoretical investigation, Eddington in 1930 published a mathematical theory of the nature of space, in which he supposed that astronomical space is not Euclidean, and that the deviation from Euclidean character depends not only on the size of the geometrical configuration considered, but also on the time that has elapsed since the creation of the world. This, which is known as the theory of the expanding universe, was generally accepted and developed for the next 23 years. Values were found for the total mass, extent, and curvature of the universe; but in 1953 a new explanation of the red-displacement was proposed by E Finlay Freundlich, and the question is still under discussion.
General Relativity
The deviations from Euclidean properties which have just been considered have a uniform character over vast regions of space. According to the theory of General Relativity, there are also deviations which vary considerably within quite small distances, and which are due to the presence of ordinary gravitating matter. Something of the kind was conjectured by the Irish mathematical physicist G F Fitzgerald when toward the end of the nineteenth century he said, "Gravity is probably due to a change of structure in the ether, produced by the presence of matter." Perhaps he thought of the change of structure as being something like change in specific inductive capacity or permeability. However, Einstein in 1915 published a definite mathematical theory, in which gravitational effects were attributed to a change in the curvature of the world, due to the presence of matter; and he showed that by this hypothesis it was possible to account for a peculiarity of the orbit of the planet Mercury which was not explained by the older Newtonian theory.
The Non-Euclidean Geometries
We shall now describe some of the features of the non-Euclidean geometries that are obtained by assuming the parallel axiom to be untrue for geometry in the plane.
If we consider a straight line and a point not on it, then either:
(1) it may be impossible to draw any straight line through that does not intersect . The geometry is then said to be elliptic.
(2) or it may be possible to draw an infinite number of straight lines through that do not intersect . The geometry is then said to be hyperbolic.
Between these possibilities there is an intermediate case, in which it is possible to draw one and only one line through P which does not intersect : this case corresponds to ordinary Euclidean geometry.
In elliptic geometry the sum of the angles of a triangle is always greater than two right angles. Every straight line, when it attains a certain length, returns into itself like the equator on a sphere, so the lengths of all straight lines are finite, and the greatest possible distance apart of two points is half this length. The perpendiculars to a straight line at all the points on it meet in a point.
In hyperbolic geometry, the sum of the three angles of a triangle is always less than two right angles; and indeed, the greater the area of the triangle, the smaller is the sum of its angles.
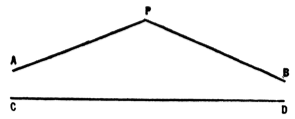
If we consider a straight line , and a point outside it, then we can draw two straight lines through and , which are not in the same straight line, with the properties that (1) any line through P which lies entirely outside the angle does not intersect the line , (2) any line through which is inside the angle intersects the line at a point at a finite distance from , (3) the two lines , tend asymptotically at one end of the line at infinity, so we may say they intersect it at infinity and are more or less analogous to Euclidean parallels: they are, in fact, called parallels to the line drawn through the point . Lines which are parallel to each other at any point are parallel along their whole length, but parallels are not equidistant: the distance between them tends to zero at one end and to infinity at the other.
Topology
The opinion that the material universe is formed of atoms, which are eternal and unchangeable, had been held by many of the ancient Greek philosophers and was generally accepted by European physicists in the nineteenth century. An attempt to account for it mathematically was made in 1887 by William Thomson (Lord Kelvin), who after seeing a display of smoke-rings in a friend's laboratory, pointed out that if the atoms of matter are constituted of vortex rings in a perfect fluid, then the conservation of matter can be immediately explained, and the mutual interaction of atoms can be illustrated. In 1876 P G Tait of Edinburgh, having the idea that different kinds of atoms might correspond to different kinds of knotted vortex rings, took up the study of knots as geometrical forms. This is a problem of a new kind, since we are not interested in the precise description of the curve of the cord, but only in the essential distinction between one kind of knot and another - the reef-knot, the bowline, the clove hitch, the fisherman's bend, etc. The transformations which change the curve of the cord but do not change the essential character of the knot were specially studied. Relations of this kind, i.e., relations which are described by such words as "external to," "right-handed," "linked with," "intersecting," "surrounding," "connected by a channel with," etc., are called topological, and the study of topological relations in general is called topology.
Another topological problem which was studied in the early days of the subject arose in connection with the flow of an electric current through a linear network of conductors. The network is a set of points (vertices) connected together in pairs by conductors. We can inquire what is the greatest number of conductors that can be removed from the network in such a way as to leave all the vertices connected together in one linear series by the remaining conductors. The number as obtained is of importance in the general problem of flow through the network.
The New Views of Axioms
It has long been realised that the axioms stated by Euclid are insufficient as a basis for Euclidean geometry; he tacitly assumes many others which are not in his list. Among these may be mentioned axioms of association, such as "if two different points of a straight line are in a plane, then all the points of the straight line are in the plane"; axioms of order, such as "of three different points lying on a straight line, one and only one lies between the other two"; and axioms of congruence, which assert the uniqueness of something - that there is only one distinct geometrical figure with certain properties: thus, a triangle is uniquely determined by two adjacent sides and the included angle.
Questions arise also regarding the use made of diagrams in geometrical proofs. In an edition of Euclid the diagrams are accurately drawn, and their topological features, which may be seen by inspection, are often essential to the proof. Thus let a diagram be drawn representing any triangle with the line bisecting its angle and the line perpendicular to its side at its middle point; if this is carelessly drawn, the point of the intersection of and might be placed inside the triangle - a topological error.
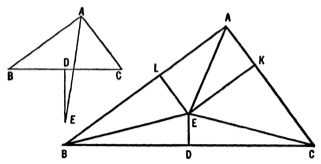
But in that case, drawing perpendiculars to and to , we can easily show that the triangles and are equal in all respects, and also the triangles and are equal in all respects, thus the angles and are equal, and the triangle is isosceles. Thus a wrong topological understanding has led to a proof that every triangle is isosceles. The axioms must therefore be such as to guard against any erroneous topological assumptions. A rigorously logical deduction of Euclidean geometry is a formidable affair.
It is of course obvious that the theorems of geometry were discovered long before strict logical proofs were found for them. Archimedes, the greatest of the Greek mathematicians, distinguishes between investigating theorems (theorein) and proving them rigorously (apodeiknunai).
When it was realised that the parallel axiom is not universally and eternally true, opinion changed about the place of axioms in mathematics. It now came to be accepted that the business of the mathematician is to deduce the logical consequences of the axioms he assumes at the basis of his work, without regard to whether these axioms are true or not; their truth or falsehood is the concern of another type of man of science - a physicist or a philosopher. Thus the horizon of the geometer was widened; instead of inquiring into the structure of actual space, he studied various different types of geometry defined respectively by their axioms: Euclidean and non-Euclidean geometries and also geometries with a finite total number of points, and what are called non-Archimedean and non-Desarguesian geometries. A non-Archimedean geometry is one which denies the "axiom of Archimedes," namely that if two segments are given, there is always a multiple of the smaller that exceeds the larger. A non-Desarguesian geometry is one in which the theorem of Desargues is not true, namely that if two triangles be such that the straight lines joining their vertices in pairs are concurrent, then the intersections of pairs of corresponding sides lie on a straight line.
The Dangers of Intuition
The recognition that an axiom is a statement which is assumed, without any necessary belief in its truth, brought a great relief to mathematicians; for intuition had led the older workers to believe in the truth of many particular assertions which were shown in the latter part of the nineteenth century to be false. The following is an example. We may for the present purpose define a continuous plane curve to be one in which, as we pass along the curve from a point to a neighbouring point , the length of the perpendicular from a point on the curve to any fixed straight line passes through all the values intermediate between the values that it has at and . Now it is obvious that a continuous curve will, in general, have a tangent at every point. But this is not always the case, as can be shown by the following construction. Take a straight line of any length, divide it into three equal parts, and on the middle part as base erect an equilateral triangle.

Delete the base of the triangle, so we are left with four segments of equal length forming a broken line. Divide each of these four segments into three equal parts, and as before erect an equilateral triangle on the middle part of each segment, and then delete the bases of these triangles, so now we have a broken line of 16 segments. Repeating this process indefinitely, we arrive in the limit at a broken line which is a definite curve, but has no tangent at any point. Examples of this kind made it impossible to accept the view generally held by Kantian philosophers, that mathematics is concerned with those conceptions which are obtained by direct intuition of space and time.
The Plan of a Rigorous Geometry
Euclid attempted to specify the subject matter of geometry by definitions such as "a point is that which has no parts" and "a straight line is a line which lies evenly with the points on itself." Neither of these definitions is made use of in his subsequent work; and indeed, the first is clearly worthless, since there exist many things besides points which have no parts, while the second is obscure.
In a modern rigorous geometry, the point and the straight line are generally accepted as undefined notions, so that the pattern of a branch of mathematics is now:
(1) enumeration of the primitive concepts in terms of which all the other concepts are to be defined
(2) definitions (i.e. short names for complexes of ideas)
(3) axioms, or fundamental propositions which are assumed without proof. It is necessary to show that they are compatible with each other (i.e. by combining them we cannot arrive at a contradiction) and independent of each other (i.e. no one of them can be deduced from the others). The compatibility is often proved by translating the assumptions into the domain of numbers, when any inconsistency would appear in arithmetical form; and the independence may be proved (as the independence of the parallel axiom was proved) by leaving out each assumption in turn and showing that a consistent system can be obtained without it.
(4) existence-theorems. The discovery of irrationals led the Pythagoreans to see the necessity for these. Does there exist a five-sided polygon whose angles are all right angles? The Greek method of proving the existence of any particular geometrical entity was to give a construction for it; thus, before making use of the notion of the middle point of a line, Euclid proves, by constructing it, that a line possesses a middle point. The "problems" of Euclid's Elements are really existence-theorems.
(5) deductions, which are the body and purpose of the work.
Space Time
Until the end of the nineteenth century it was believed that the universe was occupied by space, which had three dimensions, so that a point of it was specified by the length, breadth and height of its displacement from some point taken as origin. It was supposed that space was always the same, consisting of the same points in the same positions. Whoever might be observing it, two different observers, in motion relative to each other, would see precisely the same space. In order to specify the position of a particle at any time, it was necessary therefore to know only the three coordinates of the space-point at which it was situated, and the time. The way of measuring time was supposed to be the same for the whole universe. Events happening at different points of space were said to be simultaneous if the time coordinates of the two points were the same.
This scheme collapsed in the early years of the present century, when the theory of relativity was discovered and it was shown that observers who are in motion relative to each other do not see the same space. If we consider a particular observer, moving in any way, then for him each particle in the universe will have three definite space coordinates and a definite time coordinate; but for a different observer, moving relatively to him, both the space coordinates and the time coordinates of the particle will in general be changed. When we label every point-event of space with its coordinates as recognised by a particular observer, and also with its time as recognised by this observer, then all point-events are specified by the four coordinates , just as all points in ordinary space are specified by three coordinates . We speak of this fourfold aggregate of point-events as a four-dimensional manifold, which is called space time. If a value of t is specified, the points (t, x, y, z) which have this value of t form a three-dimensional manifold with coordinates (x, y, z), and this manifold represents a space formed of the points which are simultaneous for the observer whose time is . The problem is to find a set of equations
which rearranges the fourfold of point-events so as to convert the spaces which are simultaneous for one observer into the spaces which are simultaneous for another observer.
Numbers
Although numbers have been in use since the earliest ages, it was not until the last quarter of the nineteenth century that any satisfactory philosophical explanation was given of what they are.
Number is a property not of physical objects in themselves, but of collections or classes of objects. We must begin by explaining what we mean by saying that two classes have the same number. If we have a group of husbands and wives, and if we know that each husband has one wife and each wife has one husband, then we can affirm that the number of husbands is the same as the number of wives, even though we do not know what that number is. In other words, two classes between whose respective members a one-to-one correspondence can be set up, have the same number: to be precise, the same cardinal number, for a distinction is drawn between cardinal and ordinal numbers; ordinal numbers are defined only by reference to sets whose elements are arranged in serial order. This definition applies equally well whether the number is finite or not. Thus if two rays , , proceeding from a point , cut off segments and from two straight lines, then we can set up a one-to-one correspondence between the points of and the points of by radii , and we can say that has the same number of points as .
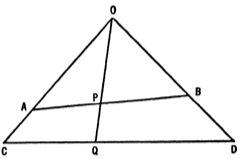
We can, however, draw lines from another point to and ; suppose that these lines cut the line in points and . Then the number of points in is the same as the number of points in , and therefore the same as the number of points in . We see therefore that in the case of infinite collections, the number of the whole is not necessarily greater than the number of the parts; and indeed, a transfinite number may be defined as the number of a collection which can be put into one-to-one correspondence with a part of itself: for example, the positive integers have a one-to-one correspondence with their squares; and, therefore, the number of the integers is equal to the number of their squares, although the squares form only a part of the whole collection of integers.
The cardinal numbers can be arranged in order by use of the notions of greater and less, which can be thus defined: a cardinal is greater than a cardinal if there is a class which has members and has a part which has members, but there is no class which has members and has a part which has members.
The addition and multiplication of two numbers can be readily defined. If and are two collections whose cardinal numbers are and , then a class formed by combining the collections and has for cardinal number the sum . If we form a new collection, of which each element consists of one element taken from , paired with one element taken from , and if these pairs are taken in all possible ways, then the cardinal number of the new collection is the product . It is readily seen that sums and products so defined satisfy
the associative law
the commutative law
and the distributive law
Transfinite Numbers
the commutative law
and the distributive law
Until seventy years ago, infinity was a somewhat vague, general concept, and mathematicians did not know that transfinite numbers of different magnitudes could be accurately defined and distinguished. Let us consider some examples of them.
Take first the rational numbers, which are the fractions representing the ratio of one whole number to another. They can be written in a rectangular array thus:
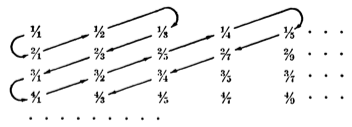
They may now be arranged in a single order by taking the diagonals of this array in turn, thus:
When they are thus ordered, they can be put in a one-to-one correspondence with the natural numbers
1, 2, 3, 4, 5, 6, 7, ... .
Any collection which can be put in a one-to-one correspondence with the natural numbers is said to be denumerable. Thus the rational numbers form a denumerable or countable set. The cardinal number of a denumerable set is the smallest transfinite cardinal number, and is denoted by . Here, aleph: is the first letter of the Hebrew alphabet.
Now let the rational numbers be arranged in order of magnitude and suppose that at a certain place in the order a division or cut is made, which causes the numbers to fall into two classes (e.g. all the rational numbers whose squares are less than 2 and all the rational numbers whose squares are greater than 2), which we shall call the left class and the right class, such that every rational number in the left class is smaller than every rational number in the right class. It may be that the right class has a least member, which will of course be a rational number, say ; or it may be that the left class has a greatest number, which will be a rational number, say . In these cases the cut is said to be made by a rational number, or as the case may be. But if the left class has no greatest member and the right class has no least member, then the cut is still regarded as being made by a number; but this will be a number of a new class, which is called an irrational number. Thus if the left and right classes are the rational numbers whose squares are respectively less and greater than 2, since there is no rational number whose square is exactly equal to 2, there will be an irrational number corresponding to the cut, and this is the number commonly represented by √2. Rational and irrational numbers are both comprehended in the name real numbers.
We have seen that the class of rational numbers is countable; but the class of real numbers, composed of rationals and irrationals together, is not countable. To prove this, suppose it to be possible that all the real numbers from 0 to 1 could be arranged in order as 1st, 2nd, 3rd, ... etc., say Suppose that these numbers are represented in the ordinary denary scale as decimals. Then we can form a new decimal in the following way: take its first digit to be any digit (from 0 to 9) different from the first digit of ; take its second digit to be any digit different from the second digit of ; take its third digit to be any digit different from the third digit of ; and so on. The number thus formed differs from all the numbers previously enumerated and it is a real number between 0 and 1; so the original enumeration cannot have contained all the real numbers between 0 and 1. By this reductio ad absurdum we see that the set of real numbers from 0 to 1 is not denumerable.
The set of real numbers is called the arithmetic continuum; by what has just been proved, the transfinite cardinal number of the arithmetic continuum is not , but a greater transfinite number, which is denoted by .
The arithmetic continuum has been constructed arithmetically, without any dependence on time and space, the two notions of the continuum with which we are intuitively familiar. If we are to assume that the arithmetic continuum is equivalent to the linear continuum, so that the motion of a particle along the line is an exact image of a numerical variable increasing from one value to another, it is evident that we must introduce an axiom, namely that there is a single point on the line corresponding to every single real number. Of course we are not bound to assume this axiom. We may assume that several points, forming an infinitesimal segment, separate the right and left classes in the proposition by which irrational numbers were defined. On this assumption, the axiom of Archimedes, to which reference was made in "The New Views of Axioms" section, would not be true.
If the Pythagorean conception of the line as made up of unit points had been correct, the ratio of any two segments of the line would have been a rational number, and there would have been no room for irrationals.
The Number of Points in a Three-Dimensional Space
One would naturally expect that the number of points in a three-dimensional region, such as the interior of a cube of side unity, would be infinitely greater than the number of points on a segment of a line, say one of the edges of the cube. But, surprisingly, this is not the case: the points in the cube can be made to correspond, point by point, with the points in its edge.
For take three of the edges, meeting at one comer, as axes of coordinates , so that for points in the cube we have three coordinates all between 0 and 1. A point on an edge can be specified by a single coordinate between 0 and 1. Now let the coordinate , which represents a particular point on the edge be expressed as a decimal, adding 0's at the end so as to make it an unending decimal. Take the 1st, 4th, 7th, etc. digits of , and write down a decimal of which these are the successive digits. Similarly write down , consisting of the 2nd, 5th, 8th, ... digits of , and write down , consisting of the 3rd, 6th, 9th, ... digits. The point of space whose coordinates are thus determined corresponds uniquely to the value of ; thus, there is a one-to-one correspondence between the points on the edge and the points inside the cube, and therefore they have the same number.
Imaginary Quantities
A work written by an Egyptian priest more than a thousand years before Christ, with the alluring title "Directions for knowing all dark things," explains how to solve various numerical problems, such as "What is the number which, when its seventh part is added to it, becomes 24?" The ancient Babylonians also proposed arithmetical puzzles, and were acquainted with arithmetic and geometric progressions. But algebra as a science can scarcely be said to have existed before the introduction of negative numbers in the early centuries of the Christian era, although results that are now commonly obtained by algebraic methods had long been known. The solution of the quadratic equation - in algebraic notation
was achieved in geometrical form by the Greek mathematicians. If the quadratic has no roots which are real numbers, it possesses algebraic roots of the form where and are real: that is, roots that are complex quantities. But the geometrical preoccupations of the Greeks led to their attention being devoted entirely to real roots, and solutions involving the "imaginary" quantity √-1 were dismissed by everybody before the sixteenth century as non-existent.
In the Renaissance, however, the Italian mathematicians discovered the solution of the cubic equation
;
their formula gave for instance the solution of the equation
as
.
In order to evaluate this, we note that
, and .
So we have the root expressed in the form
or
We have thus found a real root of the cubic, by a calculation which cannot avoid using √-1; and, this discovery compelled the mathematicians to face the question of the status of imaginary quantities. For a long time their attitude was one of mystification: the imaginary was, they said, inter Ens et non-Ens amphibium ("an amphibian between Being and non-Being").
Later it was shown to possess many important properties. Thus, many theorems were found to be true only when the numbers concerned were no longer restricted to be real: for instance, the theorem that every algebraic equation of degree n has n roots is true in general only when complex roots are taken into account. But conservatism died hard. In the latter part of the eighteenth century an English mathematician, Francis Maseres, who had been senior wrangler at Cambridge in 1752, published several tracts on algebra and theory of equations in which he refused to allow the use of "impossible" quantities.
Today, imaginary quantities are of great importance; in fact, the extensive and most useful Theory of Functions of a Complex Variable is wholly concerned with functions which depend on the quantity . It is a strange fact that as mathematics grows more abstract, it becomes more effective as a tool for dealing with the concrete - a point that was often stressed by the philosopher A N Whitehead. As an example, one may cite the very abstract theory of groups, which has many applications in the modern quantum-mechanical physics.
System of Numeration
The choice of the number 10 as the basis of our system of numeration is due to our having ten fingers; among primitive peoples the set of fingers, in which ten objects are presented in a definite order, was the natural aid to counting. Modern systems of numeration depend on the notion of place-value, with the use of the symbol zero, a plan which seems to have been introduced about 500 AD.: thus the number 5207.345 means
.
While the historical reason for the use of a decimal system is readily intelligible, it must be said that an octonary system, based on the number 8 so that 5207.345 would mean
would be more convenient. The multiplication table of the octonary system would call for only half as great an effort as is required in the decimal system; and, the most natural way of dealing with fractions is to bisect again and again, as is done for instance with brokers' prices on the stock exchange. It is perhaps unfortunate that our remote ancestors, when using their fingers for counting, included the thumbs.
Another system of numeration, which has become prominent in recent years, owing to its use in the modern electronic calculating machines, is to express numbers in "the scale of 2," or the "binary scale," in which 10110.01101 would mean
.
Symbolic Logic
Long ago Leibniz, in the course of his life as a diplomat, sometimes found himself required to devise a formula for the settlement of a dispute, such that each of the contending parties could be induced to sign it, with the mental reservation that he was bound only by his own interpretation of its ambiguities. Equivocation, such as was practiced in this connection, was, as Leibniz well knew, impossible in mathematics, where every symbol and every equation has a unique and definite meaning. And the contrast led him to speculate on the possibility of constructing a symbolism or ideography, like that of algebra, capable of doing what ordinary language cannot do, that is, to represent ideas and their connections without introducing undetected assumptions and ambiguities. He therefore conceived the idea of a logical calculus, in which the elementary operations of the process of reasoning would be represented by symbols - an alphabet of thought, so to speak - and envisaged a distant future when philosophical and theological discussions would be conducted by its means, and would reach conclusions as incontrovertible as those of mathematics. Perhaps this was too much to hope, but the actual achievements of mathematical logic have been amazing. Logic, when its power has been augmented by the introduction of symbolic methods, is capable of leading from elementary premises of extreme simplicity to conclusions far beyond the reach of the unaided reason.
The first outstanding contribution to the subject was made by George Boole, for the latter part of his life, professor in Cork, who published a sketch of his theory in 1847, and a fuller account in 1854, in his book An Investigation of the Laws of Thought. In this system, a letter such as denotes a class or collection of individual things to which some common name can be applied: for instance, might represent the class of all doctors. We can also regard as a symbol of operation, namely, the operation which selects, from the totality of objects in the world, those objects which are doctors. Now let y denote some other class, say the class of all women. Then the product must represent the result of first selecting all women, and then selecting from them those who are doctors; that is, represents all women doctors, all the individuals who belong both to the class and to the class . When, in ordinary language, a noun is qualified by an adjective, as in ''feminine doctor" we must understand the idea represented by this product.
Now consider the case when the class is the same as the class . In this case, the combination expresses no more than either of the symbols taken alone would do, so , or (since is the same as ) . In ordinary algebra, the equation is true when has either of the values zero and unity, but in Boolean algebra all symbols obey this law.
Let us now take up the question of addition. The class is defined to consist of all the individuals who belong to one at least of the classes and , whether the classes overlap or not.
The symbol used for zero in ordinary algebra is 0 used in Boolean algebra to denote the class that has no members, the null class: obviously we must have
and ,
as in ordinary algebra.
The symbol 1 is used to denote the class consisting of everything, or the "universe of discourse": it has the properties
and .
Lastly, the minus sign must be introduced: the symbol is defined to be the class consisting of those members of 1 which do not belong to , so that
and .
So far, we have interpreted Boolean algebra as an algebra of classes; but, we may take the classes to be classes of cases in which certain propositions are true, and this led to an interpretation of it as an algebra of propositions. If and are propositions, their product would represent simultaneous affirmation, so f would be the proposition which asserts "both and f": the sum would denote alternative affirmation, sof would be the proposition "either or or both." The minus sign would represent "it is not true that," so would be the proposition contrary to : the equation f would imply that is true, while the equation , which is equivalent to , would signify that f is false. The equation would now represent the logical principle of the excluded middle, that every proposition is either true or false, and the equation would represent the principle of contradiction.
Peano's Symbolism
Boole used only the ordinary algebraic symbols: the symbol ×, which in ordinary algebra represents multiplication, may be said to correspond in Boolean algebra to the word and, while the symbol of addition, +, corresponds to or, and the symbol of a negative quantity, -, corresponds to not. The great development of such ideas took place in the last years of the nineteenth century, when Giuseppe Peano, professor at the University of Turin, invented a new ideography for use in symbolic logic. He introduced new symbols to represent other logical notions, such as "is contained in," "the aggregate of all 's such that," "there exists," "is ," "the only," etc. For example, the phrase "is the same thing as" is represented by the sign =, while the symbol
One of the elementary processes of logic consists in deducing from two propositions, containing a common element or middle term, a conclusion connecting the two remaining terms. This corresponds to the process of elimination in algebra and may be performed in a way roughly analogous to it. The parallelism of logic and algebra is indeed far reaching: for instance, the logical distinction between categorical propositions and conditional propositions corresponds closely to the algebraical distinction between identities and equations. Again, the inequalities of algebra have their analogues in logic. Consider, for instance, the statement that if a proposition implies a proposition , and implies a proposition , then implies . This bears an obvious resemblance to the algebraical theorem that if is less than , and f is less than , then is less than . It is useful to have a symbol which represents logical implication or inclusion, and all modern forms of symbolic logic do in fact employ one or two, one in the calculus of propositions and one in the calculus of classes. This however, does not represent an independent concept, but can be defined in terms of the logical product; for the statement that is included in, or implies, , is equivalent to the statement that the logical product of and is equal to .
Peano's ideograms represent the constitutive elements of all the other notions in logic, just as the chemical atoms are the constitutive elements of all substances in chemistry; and they are capable of replacing ordinary language completely for the purposes of any deductive theory.
The Developments of Whitehead and Russell
In 1900 A N Whitehead and Bertrand Russell, both of Cambridge, went to Paris to attend the congresses in mathematics and philosophy which were being held in connection with the International Exhibition of that year. At the Philosophical Congress they heard an account of Peano's system and saw that it was vastly superior to anything of the kind that had been known previously. They resolved to devote themselves for years to come to its development, and, in particular, to try to settle by its means the vexed question of the foundations of mathematics.
The thesis which they now set out to examine, and if possible to prove, was that mathematics is a part of logic: it is the science concerned with the logical deduction of consequences from the general premises of all reasoning, so that a separate "philosophy of mathematics" simply does not exist. This of course contradicts the Kantian doctrine that mathematical proofs depend on a priori forms of intuition, so that, for example, the diagram is an essential part of geometrical reasoning. Whitehead and Russell soon succeeded in proving that the cardinal numbers 1, 2, 3, ... can be defined in terms of concepts which belong to pure logic, such as class, implication, negation, and which can be represented by Peano ideograms. From this first success they advanced to the investigations published in the three colossal volumes of Principia Mathematica, which appeared in 1910-1913 and contain altogether just under 2,000 pages.
It was admitted that for mathematical purposes certain axioms must be adjoined to those that are usually found in treatises on logic, e.g., the intuition of the unending series of natural numbers, which leads to the principle of mathematical induction; but this extension of logic did not affect the main position.
The growth of logic, which had been at a standstill for the two thousand years from Aristotle to Boole, has progressed with amazing vitality from Boole to the present day. It is remarkable that some of the errors of Aristotle remained undetected until the recent developments. Consider, for instance, his doctrine that "in universal statement the affirmative premise is necessarily convertible as a particular statement, so that for example from the premise all dragons are winged creatures, follows the consequence some winged creatures are dragons. The premise is unquestioned, but Aristotle's deduction from it asserts the existence of dragons. Now it is evident that the existence of dragons cannot be deduced by pure reason and, therefore, Aristotle's general principle must be wrong. The most important advance, however, was not the detection of the errors of the old logic, but the removal of its limitations. The Aristotelian system in effect took into account only subject-predicate types of propositions, and failed to deal satisfactorily with reasoning in which relations were involved, such as "If there is a descendant, there must be an ancestor." It was not possible to reduce to an Aristotelian syllogism the inference that if most have coats and most have waistcoats, then some must have both coats and waistcoats. In this and other respects the subject has become enlarged to such an extent that only a comparatively small part of any modern treatise is devoted to the traditional logic.
Whitehead and Russell's work may without exaggeration be described as the foundation of the modern renaissance in logic, which, as the successive volumes of the Journal of Symbolic Logic show, is now chiefly centred in America. A notable feature of it is the development of what Hilbert has called metamathematics, that is, of theorems about theorems. An example is the result found in 1931 by Gödel, that there are some propositions of mathematics which, though they have a meaning, cannot be either proved or disproved by means of any system based on axioms, such as that of Principia Mathematica.
Russell's Paradox
The advantages of an ideography as compared with ordinary language are strikingly evident in the discussion of certain contradictions which have threatened to invalidate reasoning, such as a famous paradox that was discovered fifty years ago by Bertrand Russell. He remarked that in the case of e.g., the class whose members are all thinkable concepts, the class, being itself a thinkable concept, is one of its own members. This is not the case with e.g., the class of all blue objects, since this class is not itself blue. We can therefore say that those classes which do not contain themselves as one of their members form a particular kind of classes. The aggregate of these classes constitutes a new class which we shall call . Let us put this definition in the two forms:
Form . A class which contains itself as a member is not a member of .
Form . A class which does not contain itself as a member is a member of . Now if were a member of itself, then by it would not be a member of itself, so we should have a contradiction; while if were not a member of itself, then by it would be a member of itself, which is again a contradiction. Thus on either supposition we arrive at a contradiction, which appears to be insoluble by any kind of verbal explanation.
Now let us look at the matter from the point of view of symbolism. The contradiction that " is an x" is equivalent to " is not an " was obtained essentially by substituting for in the statement that (1) is a class (2) is an , is equivalent to " is not a ." This substitution, however, is not, as it stands, an operation performed on the fundamental logical symbols in accordance with the rules which are laid down for operating on them; for, is not itself one of the elementary ideograms, but is an abbreviation, a single letter standing proxy for a complex of ideas. Now all abbreviations, however convenient, are from the logical point of view superfluous; and an argument involving them is not valid unless, at every stage of it, the proxy symbols can be replaced by the full expressions for which they stand. In order therefore to be sure that what has been done is correct from the point of view of symbolic logic, we must translate the whole argument, and in particular the operation of substituting for , into the language of the elementary ideograms and the operations that are permissible with them, so that all explicit mention of will have been eliminated from the proof. When, however, we try to do this, we find that we cannot. It is not possible to state Russell's paradox in the form of an assertion composed solely of the elementary ideograms. This shows that if we had from the beginning avoided the use of ordinary speech or of proxy symbols and conducted all our investigations according to the strict precepts of ideography, then Russell's paradox would never have emerged. It can be obtained by argumentation in words, or it can be obtained by a quasi-symbolic argument in which an operation is permitted which is untranslatable into pure symbolic logic; but it cannot be obtained by any process which is restricted to using throughout nothing but the elementary ideograms and the operations that are recognised as permissible with them, and which express both the final result and all intermediate equations in terms of them exclusively. Thus Russell's paradox, being inexpressible in symbolic logic, is really meaningless, and we need not concern ourselves with it further. The contradiction which appears in it is not inherent in logic, but originates in the imperfections of language and of abbreviated symbolism.
The Intuitionists
The Whitehead-Russell doctrine that mathematics is based on logic is opposed by a school led by the Dutch mathematician L E J Brouwer and the German Hermann Weyl, and known as intuitionists, who maintain the contrary view, that logic is based on mathematics. The series of natural numbers is held to be given intuitively and to be the foundation of all mathematics, so that numbers are not derived, as Russell supposed, from logic. Their system contains a new feature which may be explained thus.
Let it be asked whether, in the development of π as a decimal fraction, there is a place where a particular digit, say 5, occurs ten times in succession. It is of course conceivable that by performing the actual development we might come upon such a succession; or it is conceivable that a general proof might show that it cannot happen; but these two solutions evidently do not exhaust all the possibilities. Under these circumstances, Brouwer and Weyl decline to pronounce the disjunctive judgment of existence, that the development of π as a decimal either does or does not include a succession of ten 5's; in other words, they assert that the logical principle of the excluded middle, that every proposition is either true or false, is not valid in domains where a conclusion one way or the other cannot be reached in a finite number of steps. They replace the notion of true by verifiable and call propositions false only if their contradictory is verifiable. This position leads them to abandon the attempt to justify large parts of traditional mathematics: in particular, they reject all proofs by reductio ad absurdum (which generally depend on the law of the excluded middle) and all propositions involving infinite collections or infinite series. The disastrous consequences to mathematical analysis of adopting such a position have prevented it from gaining any general acceptance, but it is not easy to disprove.
Probability
In 1654 some one proposed to Blaise Pascal the following problem: a game between two players of equal skill is discontinued for some reason before it is finished: given the scores attained at the time of the stoppage, and the full score required for a win, in what proportion should the stakes be divided? Pascal communicated the problem to his friend Pierre de Fermat, and the two in finding the solution created the theory of probability.
Like any other branch of pure mathematics, the theory of probability begins with undefined notions, and axioms. We consider a trial, such as drawing a card out of a pack, in which different possible events (the drawing of particular cards) might occur, and we introduce the undefined notion of probability, which may be described as a numerical measure of quantity of belief that one particular event will happen, i.e., that some named card will be drawn. The axiom on which the theory is based may be stated thus: In a given trial let A and B be two events which cannot possibly happen together; then the probability that either A or B will happen is the sum of the probabilities of their happening separately.
Thus in tossing a coin, let be the probability of heads and the probability of tails. Then on account of the symmetry of the coin we may assume that . Moreover, from the axiom we see that is the probability that either heads or tails will fall; but this latter is a certainty, to which we give our entire belief. It is convenient to measure entire belief by the number unity: so we have
,
and therefore . The probability of heads in a single toss of a coin is .
In practically all the calculations that we can make, some use is made of a property of symmetry: thus, a die is a cube, symmetrical with respect to all its six faces, so the probability that when cast it will show a particular specified face is ; a pack has 52 cards which are equally likely to be drawn, so the probability of drawing, say, the ace of spades, is .
The axiom can readily be extended in the form: the probability of an event is the ratio of the number of favourable cases to the number of possible cases, when all cases are supposed (generally for reasons of symmetry) to be equally likely. Thus, suppose an old man has only two teeth: what is the probability that they will meet? In this case, whatever position one of the teeth occupies, there are 31 possible positions for the other tooth, and of these only one is favourable. There the required probability is .
It is, however, easy to make mistakes through not taking sufficient care in enumerating the equally likely cases. Thus, take the following argument, which appeared in a recent book: ''The sum of an odd number and an even number is an odd number, while the sum of two odd numbers is an even number, and so is the sum of two even numbers. Hence if two numbers are chosen at random, the probability that their sum will be even is twice the probability that it will be odd." The error here comes from not recognising that there are four equally likely cases, namely, ; of these, two are favourable to an even sum and two to an odd sum, so the probabilities of an odd and an even sum are really equal.
A well-known problem is that of the "Yarborough," i.e., the probability that a hand, which is obtained when an ordinary pack of cards is dealt between four players, should contain no card higher than a nine. The probability is nearly ; a former Earl of Yarborough is said to have done very well for himself by betting 1000 to 1 against its happening.
Although the difficulty of probability problems as regards mathematical symbolism is usually not great, they are often very puzzling logically. The reader may like to try the following: given an assertion, , which has the probability , what does that probability become, when it is made known that there is a probability that is a necessary consequence of having the probability ?
The answer is
A problem which has some bearing on the credibility of evidence is the following: let be the a priori probability of an event which a witness has asserted to have happened; and let the a priori probabilities that he would choose to assert it be on the supposition of its being true, and on the supposition of its being false. What, after his assertion, is the probability that it really happened? The answer is
We see that however small may be, the value of this fraction may approach indefinitely near to unity - that is, the probability that the event happened may approach certainty - provided be much less than : that is, provided the fact of the assertion may be much more easily accounted for by the hypothesis of its truth than of its falsehood. We must not let ourselves be influenced unduly by the antecedent improbability of an event but must think out the consequences of the contrary hypothesis, which may be more improbable still.
Statistics
One of the most important applications of the theory of probability is to questions regarding statistics, which have to be dealt with specially by actuaries, astronomers, and social workers. The connection between probability and statistics is indicated by a theorem established in 1713 by James Bernoulli, which may be thus stated: let be the probability of the happening of an event in a single trial, and let be the number of times the event is observed to happen in trials, so may be called the statistical frequency; then as increases indefinitely, the probability approaches certainty that the statistical frequency will approach .
This law suggests that we should study what happens when the number of trials is limited, though great, and should calculate the probability of the deviations of the statistical frequency from p which then occur. The calculation is not difficult, and leads to definite laws of frequency of error. These are the basis of the methods used e.g. in astronomy for combining observations so as to find the most probable value of a set of quantities from a number of discordant observations of them.
If an event happens only rarely, the formula for the probability of occurrences in trials is different. It has been verified by comparison with the statistical frequency in such different cases as the number of deaths from the kicks of horses in the Prussian Army, and the number of alpha-particles falling on a screen in unit time in certain experiments with radioactive substances.
The theory of statistics is much concerned with what is called correlation, which may be explained thus. Consider a definite group containing a large number of men and let be some measurable attribute of a man, say his height, while is another measurable attribute, say his weight. Let the values of these attributes for a man be indicated by a dot whose coordinates are and in a diagram. The dots corresponding to all the men will cluster round a certain point which represents the mean height and weight. Now take axes , through . We know that in general a tall man will also be a heavy man, and therefore a positive deviation of from the mean will most often be associated with a positive deviation of , and similarly a negative deviation of will generally be associated with a negative deviation of .
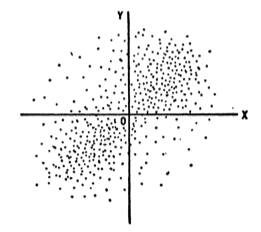
That is to say, the dots will lie chiefly in the first and third quadrants of the diagram. In such a case we say that there is correlation between the two attributes and . It can be measured by a coefficient of correlation, whose value can be calculated by forming the sums of the values of , and , for all the points in the diagram.
Stochastic Systems
The principle of causality is expressed by the assertion that whatever has begun to be, must have had an antecedent or cause which accounts for it. This principle is not violated by events of the kind that has usually been studied in works on probability. Consider for instance the tossing of a coin: we do not know on which side the coin will come down, but that is because we do not know all the circumstances of its projection - the mass and shape of the coin, the force applied by the thumb of the operator, etc. We do not doubt that if all these data were available to us, it would be theoretically possible to calculate completely the behaviour of the coin, and to predict the side on which it would come down; and, therefore, our lack of ability to make this prediction is due only to our ignorance and not to any failure of determinism in nature. Systems whose working is really governed by strict law, but whose performance we cannot foretell for want of knowledge, are said to have hidden parameters: if we knew all about the hidden parameters, we should be able to predict everything.
In the newer physics, we have phenomena like the spontaneous breakup of a radium atom, in which an alpha-particle is given off and the atom is transformed into an atom of radium emanation. It is not possible to foretell the instant when any particular radium atom will disintegrate; and, it was formerly supposed that this is because a radium atom contains hidden parameters - perhaps the positions and velocities of the neutrons and protons inside the nucleus - which are not known to us and which determine the time of the explosion. For reasons which belong to physics and therefore would not be in place here, it is now generally recognised that these hidden parameters do not exist. The disintegrations do not occur in a deterministic fashion, and the only knowledge which is even theoretically possible regarding the time of disintegration is the probability that it will happen within (say) the next year. A system in which events such as disintegrations take place according to a law of probability, but are not individually determined in accordance with the principle of causality, is said to be a stochastic system. The fact that the systems considered in microphysics are largely stochastic systems make the theory of probability of fundamental importance in the application of mathematics to the study of nature.
Conclusion: The Philosophy of Mathematics and the Philosophy of Science
This talk on mathematics may end with an attempt to answer the question, how is progress in mathematics related to progress in the other sciences?
We have seen that a very high standard was attained in mathematics as early as the fourth and third centuries before Christ; the Elements of Euclid are sufficient to carry the modern student of geometry to the point where university courses begin. No comparable development was reached in any other branch of science for 2000 years. Why was this?
In the generation immediately before Euclid, as we have seen, the philosopher Aristotle, whose scientific interests were in biology rather than in mathematics, tried to find a general method of adding to knowledge, by creating the science of logic, which he brought to the form in which it remained with little change until the present age. In showing how logic might be used to advance discovery, Aristotle relied chiefly on the syllogistic type of reasoning that had been so successful in geometry. But syllogisms must start from certain basic truths which are accepted as premises; and it was in the methods of finding these basic truths that Aristotle's scheme was weakest. He collected a great number of observations but does not seem to have taken care to reject those that could not be verified, and he never designed an experiment for the purpose of testing a hypothesis. Syllogisms are as a rule comparatively unimportant in the non-mathematical sciences, and the great place given to them in logic led the later Aristotelians to attach undue importance to mere words.
In the thirteenth century, the influence of Aristotle was greatly increased by the work of St Thomas Aquinas; but, so far as science was concerned, Aristotelianism developed in a completely sterile form and a violent reaction against it set in, the leaders of which were Galileo (1564-1642) and Bacon (1561-1626). Bacon emphasised the importance of induction from observation and the necessity for experiment, though even in Bacon we do not find any recognition of the necessity for framing hypotheses and then designing experiments to test them. This indeed can hardly be said to have figured as a doctrine of philosophers until it had become the practice of the great men of science of the seventeenth century, particularly of Isaac Newton (1642-1727). The outstanding characteristic of the Newtonian philosophy was its focusing of interest on the changes that occur in the objects considered. The Greek philosophers had marked the distinction between mathematics and physics by assigning to the mathematician the study of entities which are conserved unchanged in time, and to the physicist the study of those entities which undergo variations; but Newton created a type of mathematics in which the calculation of rates of change was fundamental. The rate of change of position of a body moving in a straight line, which is called its velocity, and the rate of change of the velocity, which is called its acceleration, were now studied. Newton regarded a curve as generated by the motion of a point, a surface by the motion of a curve, and so on. The quantity generated was called the fluent, and the motion was defined by what he called the fluxion; and he showed that when a relation was given between two fluents, the relation between their fluxions could be found, and conversely. This theory of fluxions, known later as the infinitesimal calculus, became the major occupation of the mathematicians of the eighteenth and nineteenth centuries, and led to wonderful advances in the study of nature.