Avi Wigderson Awards
Avi Wigderson has received many awards including: the Bergman Fellowship (1989); the Yoram Ben-Porat Presidential Prize for Outstanding Researcher (1994); the Rolf Nevanlinna Prize (1994); the Levi L Conant Prize (2008); the Gödel Prize (2009); the Donald E Knuth Prize (2019); and the Abel Prize (2021). We give some information about each of these below. In this, when shared prizes are given, we omit those parts of the citation, and other sources, that relate directly to those other than Wigderson.
Click on a link below to go to that prize
Click on a link below to go to that prize
- The Yoram Ben-Porat Presidential Prize for Outstanding Researcher (1994)
- The Rolf Nevanlinna Prize (1994)
- The Levi L Conant Prize (2008)
- The Gödel Prize (2009)
- The Donald E Knuth Prize (2019)
- The Abel Prize (2021)
- The Turing Award (2023)
1. The Yoram Ben-Porat Presidential Prize for Outstanding Researcher (1994).
Yoram Ben-Porat (1934-1992) was an Israeli economist who became president of the Hebrew University of Jerusalem in 1990. He died in an automobile accident in October 1992 and the Yoram Ben-Porat Presidential Prize for Outstanding Researcher was set up in his memory. It was awarded to Avi Wigderson in 1994 when he Chairman of the Computer Science Institute of the Hebrew University of Jerusalem.
2. The Rolf Nevanlinna Prize (1994).
2.1. The International Congress of Mathematicians.
The International Congress of Mathematicians was held from 3 to 11 August 1994 in Zurich, Switzerland. The International Mathematical Union set up the following committee to choose the winner of the Rolf Nevanlinna Prize. The Rolf Nevanlinna Prize Committee consisted of Jacques-Louis Lions (Chairman), H W Lenstra, R Tarjan, M Yamaguti and J Matiyasevic. At the end of the Opening Ceremony of the Congress, Avi Wigderson received his Prize. Prof Jacques-Louis Lions, Chairman of the Rolf Nevanlinna Prize Committee, announced Avi Wigderson as the recipient of the Rolf Nevanlinna Prize; the prize winner received his prize from Prof B Eckmann.
2.2. Avi Wigderson receives the Rolf Nevanlinna Prize.
Avi Wigderson was awarded the Rolf Nevanlinna Prize:-
I am to present the research performed by Professor Avi Wigderson. This is both a pleasant and a difficult errand, and there are two sources of this difficulty.
First, Avi Wigderson has made a lot of wonderful contributions to diverse areas of the mathematical foundations of computer science. I have time to outline only a few of them. The selection is entirely mine. If another member of the Committee were chosen for this presentation, he well might speak about different works of Avi Wigderson. The choice is indeed very large.
The second source of difficulty in presenting Avi Wigderson's works is due to the fact that in many cases they are based on complex well-balanced definitions that are too technical to be reproduced here (the balance is often between a statement to be uninteresting or to be not true). That is why my presentation will be on informal, intuitive level.
Some of Avi Wigderson's impressive results are connected with the so-called zero-knowledge interactive proofs. This was a new and rather paradoxical kind of mathematical evidence introduced by Goldwasser, Micali, and Rackoff. A zero-knowledge interactive proof allows a mathematician A, called the Provcr, to convince another mathematician B, called the Verifier, that a certain mathematical statement is true without providing a formal proof, and moreover, without giving any hints as to such a proof.
For example, suppose that mathematician A established that some large integer is composite by finding its nontrivial factorisation . Now he or she can, in a dialog with another mathematician B, convince the latter that is indeed composite but without revealing the values of the factors.
Of course, in mathematics there cannot be a secret in the strong sense. As soon as two mathematicians have agreed on the axioms and on the rules of logical deduction, it is only a matter of time and space to find a proof for any provable statement. Speaking more technically, zero-knowledge means that the amount of the work required for the Verifier to find an actual proof after the dialog with the Prover is on average essentially the same as it was before the dialog.
In fact, an interactive proof is not a proof in the strong sense because such a proof can be given, in principle, even to a statement that is not true at all. However, the probability of such a misproof goes to zero exponentially with the number of questions asked and hence the probability of giving an interactive "proof for a false statement can be easily made arbitrarily small. This is just what gives the convincing power to interactive proofs.
For such a convincing but zero-knowledge proof to become possible, the Prover and the Verifier should agree in advance upon what kinds of questions can be asked. In technical terms such an agreement is called protocol.
When the notion of zero-knowledge was first introduced, zero-knowledge protocols were known only for statements of a rather restricted nature. The actual scope of zero-knowledge proofs remained unclear. Avi Wigderson, in collaboration with Goldreich and Micali, established the following fundamental fact: zero-knowledge proofs are possible for so-called class NP. This class is one of the main subjects of study in modern computer science. Roughly speaking, class NP consists of statements that become easy to verify when a small amount of additional information is supplied.
This result on the existence of zero-knowledge proofs for class NP was based on the conjecture of the existence of so called one-way functions. Roughly speaking, is such a function if it is easy to calculate its value for given but it is difficult to find an for given . For example, it is easy to calculate an integer from its prime factorization but it is believed to be a difficult task to factor a large integer.
However, nobody has proved so far that factoring is in fact a difficult task. Moreover, the existence of a single one-way function has not been proved so far. Nevertheless, it is a widely accepted conjecture used almost as an axiom and hence its use was completely justified. However, Avi Wigderson, in collaboration with Ostrovski, also studied what would follow from the nonexistence of one-way functions. They established that the assumption of the existence of one-way functions was indeed essential for the existence of nontrivial zero-knowledge interactive proofs.
This is so for the original type of interactive proofs. Wishing still to avoid the yet unproved conjecture, Avi Wigderson in collaboration with Ben-Or, Goldwasser, and Kilian, introduced a new kind of interactive proof. In such multi-prover interactive proofs two or more persons convince another one by conversation with the latter. In this scheme the Verifier cannot check whether the answers are correct but he or she can check that the answers from different Provers are consistent. That is why the Verifier should be sure that during the interactive proof there is no exchange of information among the Provers, and this non-mathematical assumption replaces the yet unproved conjecture on the existence of one-way functions.
(This difference between single-user and multi-user interactive proofs can be viewed as mathematical justification of the saying "Two heads are better than one" which seems to have counterparts in many languages. In a sense, almost all papers of Avi Wigderson contribute to the justification of such sayings, at least with respect to mathematics, because almost all his papers were written in collaboration with other mathematicians.)
Zero-knowledge proofs are a very interesting subject of study by themselves but they have also found numerous applications, in particular, for fault-tolerant distributed computations. Such computations involve several communicating agents, some of whose work could be faulty. In this area we found
A TYPICAL THEOREM. A particular computational task can be achieved by a computational network of participating agents provided that strictly fewer than of them are faulty.
Avi Wigderson, in collaboration with Goldwasser and Ben-Or and with Goldreich and Micali, obtained very general results of this kind. These results are striking in two aspects. First, they are uniform; namely, the values of do not depend on the particular computational task (but may vary for different assumptions about the network). Second, the values of obtained are the best possible, namely, given exactly or more faulty agents, there exist computations that cannot be accomplished.
Interactive proofs use randomness in an essential way. (Clearly, the Prover must be unable to predict the forthcoming questions of the Verifier.) For a long time randomness has been recognised as a specific computational resource. Avi Wigderson contributed to the study of the computational power of randomness and to the construction of pseudo-random generators.
Formal definition of zero-knowledge, of what constitutes a good pseudo-random generator, and definitions of many other important concepts are based on estimates of the amount of computational work required for particular tasks. Such estimates depend heavily on the computational model used, and here Avi Wigderson shows his universal capacities. He contributed to both lower and upper bounds on the complexity of computations on very different computational devices: from powerful parallel computers to very restricted Boolean circuits. While nontrivial upper bounds are of practical interest, the lower bounds in this area are usually much more difficult to prove. In fact, to get an upper bound one needs to find only one algorithm, let ingenious, whereas to get a lower bound one has to observe in some way all conceivable algorithms for a particular task.
Avi Wigderson's more recent investigations are connected with computational aspects of special dynamical systems motivated by genetic algorithms and kinetic gas models. Here he had already contributed to transferring to nonlinear systems results that previously were known only in the linear case. I do not doubt that soon we shall hear about his new striking results in this area as well.
3. The Levi L Conant Prize (2008).
The International Congress of Mathematicians was held from 3 to 11 August 1994 in Zurich, Switzerland. The International Mathematical Union set up the following committee to choose the winner of the Rolf Nevanlinna Prize. The Rolf Nevanlinna Prize Committee consisted of Jacques-Louis Lions (Chairman), H W Lenstra, R Tarjan, M Yamaguti and J Matiyasevic. At the end of the Opening Ceremony of the Congress, Avi Wigderson received his Prize. Prof Jacques-Louis Lions, Chairman of the Rolf Nevanlinna Prize Committee, announced Avi Wigderson as the recipient of the Rolf Nevanlinna Prize; the prize winner received his prize from Prof B Eckmann.
2.2. Avi Wigderson receives the Rolf Nevanlinna Prize.
Avi Wigderson was awarded the Rolf Nevanlinna Prize:-
... for his outstanding work on the mathematical foundations of computer science. The objects of research there include, for example, finding efficient methods for solving complex tasks as well as upper and lower bounds for the computational effort for certain problems. Wigderson made a significant contribution to understanding the paradoxical term "zero-knowledge interactive proofs."2.3. Extracts from Yuri Matiyasevich on Wigderson's research.
I am to present the research performed by Professor Avi Wigderson. This is both a pleasant and a difficult errand, and there are two sources of this difficulty.
First, Avi Wigderson has made a lot of wonderful contributions to diverse areas of the mathematical foundations of computer science. I have time to outline only a few of them. The selection is entirely mine. If another member of the Committee were chosen for this presentation, he well might speak about different works of Avi Wigderson. The choice is indeed very large.
The second source of difficulty in presenting Avi Wigderson's works is due to the fact that in many cases they are based on complex well-balanced definitions that are too technical to be reproduced here (the balance is often between a statement to be uninteresting or to be not true). That is why my presentation will be on informal, intuitive level.
Some of Avi Wigderson's impressive results are connected with the so-called zero-knowledge interactive proofs. This was a new and rather paradoxical kind of mathematical evidence introduced by Goldwasser, Micali, and Rackoff. A zero-knowledge interactive proof allows a mathematician A, called the Provcr, to convince another mathematician B, called the Verifier, that a certain mathematical statement is true without providing a formal proof, and moreover, without giving any hints as to such a proof.
For example, suppose that mathematician A established that some large integer is composite by finding its nontrivial factorisation . Now he or she can, in a dialog with another mathematician B, convince the latter that is indeed composite but without revealing the values of the factors.
Of course, in mathematics there cannot be a secret in the strong sense. As soon as two mathematicians have agreed on the axioms and on the rules of logical deduction, it is only a matter of time and space to find a proof for any provable statement. Speaking more technically, zero-knowledge means that the amount of the work required for the Verifier to find an actual proof after the dialog with the Prover is on average essentially the same as it was before the dialog.
In fact, an interactive proof is not a proof in the strong sense because such a proof can be given, in principle, even to a statement that is not true at all. However, the probability of such a misproof goes to zero exponentially with the number of questions asked and hence the probability of giving an interactive "proof for a false statement can be easily made arbitrarily small. This is just what gives the convincing power to interactive proofs.
For such a convincing but zero-knowledge proof to become possible, the Prover and the Verifier should agree in advance upon what kinds of questions can be asked. In technical terms such an agreement is called protocol.
When the notion of zero-knowledge was first introduced, zero-knowledge protocols were known only for statements of a rather restricted nature. The actual scope of zero-knowledge proofs remained unclear. Avi Wigderson, in collaboration with Goldreich and Micali, established the following fundamental fact: zero-knowledge proofs are possible for so-called class NP. This class is one of the main subjects of study in modern computer science. Roughly speaking, class NP consists of statements that become easy to verify when a small amount of additional information is supplied.
This result on the existence of zero-knowledge proofs for class NP was based on the conjecture of the existence of so called one-way functions. Roughly speaking, is such a function if it is easy to calculate its value for given but it is difficult to find an for given . For example, it is easy to calculate an integer from its prime factorization but it is believed to be a difficult task to factor a large integer.
However, nobody has proved so far that factoring is in fact a difficult task. Moreover, the existence of a single one-way function has not been proved so far. Nevertheless, it is a widely accepted conjecture used almost as an axiom and hence its use was completely justified. However, Avi Wigderson, in collaboration with Ostrovski, also studied what would follow from the nonexistence of one-way functions. They established that the assumption of the existence of one-way functions was indeed essential for the existence of nontrivial zero-knowledge interactive proofs.
This is so for the original type of interactive proofs. Wishing still to avoid the yet unproved conjecture, Avi Wigderson in collaboration with Ben-Or, Goldwasser, and Kilian, introduced a new kind of interactive proof. In such multi-prover interactive proofs two or more persons convince another one by conversation with the latter. In this scheme the Verifier cannot check whether the answers are correct but he or she can check that the answers from different Provers are consistent. That is why the Verifier should be sure that during the interactive proof there is no exchange of information among the Provers, and this non-mathematical assumption replaces the yet unproved conjecture on the existence of one-way functions.
(This difference between single-user and multi-user interactive proofs can be viewed as mathematical justification of the saying "Two heads are better than one" which seems to have counterparts in many languages. In a sense, almost all papers of Avi Wigderson contribute to the justification of such sayings, at least with respect to mathematics, because almost all his papers were written in collaboration with other mathematicians.)
Zero-knowledge proofs are a very interesting subject of study by themselves but they have also found numerous applications, in particular, for fault-tolerant distributed computations. Such computations involve several communicating agents, some of whose work could be faulty. In this area we found
A TYPICAL THEOREM. A particular computational task can be achieved by a computational network of participating agents provided that strictly fewer than of them are faulty.
Avi Wigderson, in collaboration with Goldwasser and Ben-Or and with Goldreich and Micali, obtained very general results of this kind. These results are striking in two aspects. First, they are uniform; namely, the values of do not depend on the particular computational task (but may vary for different assumptions about the network). Second, the values of obtained are the best possible, namely, given exactly or more faulty agents, there exist computations that cannot be accomplished.
Interactive proofs use randomness in an essential way. (Clearly, the Prover must be unable to predict the forthcoming questions of the Verifier.) For a long time randomness has been recognised as a specific computational resource. Avi Wigderson contributed to the study of the computational power of randomness and to the construction of pseudo-random generators.
Formal definition of zero-knowledge, of what constitutes a good pseudo-random generator, and definitions of many other important concepts are based on estimates of the amount of computational work required for particular tasks. Such estimates depend heavily on the computational model used, and here Avi Wigderson shows his universal capacities. He contributed to both lower and upper bounds on the complexity of computations on very different computational devices: from powerful parallel computers to very restricted Boolean circuits. While nontrivial upper bounds are of practical interest, the lower bounds in this area are usually much more difficult to prove. In fact, to get an upper bound one needs to find only one algorithm, let ingenious, whereas to get a lower bound one has to observe in some way all conceivable algorithms for a particular task.
Avi Wigderson's more recent investigations are connected with computational aspects of special dynamical systems motivated by genetic algorithms and kinetic gas models. Here he had already contributed to transferring to nonlinear systems results that previously were known only in the linear case. I do not doubt that soon we shall hear about his new striking results in this area as well.
3.1. The Prize winning paper.
The American Mathematical Society awards the Levi L Conant Prize for outstanding expository papers published in the Bulletin of the American Mathematical Society or the Notices of the American Mathematical Society in the previous five years. Shlomo Hoory, Nathan Linial and Avi Wigderson received the 2008 Levi L Conant Prize for their paper "Expander graphs and their applications", Bulletin of the American Mathematical Society 43 (4) (2006), 439-561.
3.2. From a review of "Expander graphs and their applications".
Mark R Jerrum writes in a review of Expander graphs and their applications:-
Avi Wigderson is a professor at the School of Mathematics, Institute for Advanced Study (IAS), Princeton. He obtained his B.Sc. in computer science from the Technion in 1980 and his Ph.D. from Princeton in 1983. He was a member of the faculty at the Hebrew University in Jerusalem from 1986 to 2003. He joined the permanent faculty of the IAS in 1999. His research interests lie principally in complexity theory, algorithms, randomness, and cryptography. His awards include the Nevanlinna Prize (1994).
3.4. Conant Prize Response of Avi Wigderson.
I am honoured to receive the Conant Prize for my joint paper with Shlomo Hoory and Nati Linial. Many thanks are in order. First and foremost, to Nati and Shlomo for the pleasure of teaching together (at the Hebrew University) the course which resulted in this manuscript and for the big effort of writing it. Thanks to the many students of this course whose scribe notes formed the foundation of that paper. Special thanks to Mark Goresky, who convinced us to write it and whose enthusiasm and meticulous reading of earlier drafts helped get us through the process. Thanks to the many others who read and corrected earlier versions. And finally, thanks to the many colleagues and collaborators from whom I learned so much in the wonderful world of expander graphs.
4. The Gödel Prize (2009).
The American Mathematical Society awards the Levi L Conant Prize for outstanding expository papers published in the Bulletin of the American Mathematical Society or the Notices of the American Mathematical Society in the previous five years. Shlomo Hoory, Nathan Linial and Avi Wigderson received the 2008 Levi L Conant Prize for their paper "Expander graphs and their applications", Bulletin of the American Mathematical Society 43 (4) (2006), 439-561.
3.2. From a review of "Expander graphs and their applications".
Mark R Jerrum writes in a review of Expander graphs and their applications:-
True to its title, this excellent article is both a thorough exposition of expander graphs and the mathematics surrounding them and a survey of the surprisingly wide range of applications of expander graphs, particularly in complexity theory and coding theory. Naturally enough, the relationship between expansion properties of a graph and the spectrum of its adjacency matrix (more particularly the gap between the two largest eigenvalues) is a theme running throughout the article. The topics covered are too numerous to list in their entirety here, but include: mixing rate of random walks on graphs, reducing or eliminating randomness in algorithms, Ramanujan graphs, explicit constructions, error correcting codes and metric embedding. The coverage is up-to-date, including, for example, the "zig-zag product" of graphs and its applications.3.3. Conant Prize Biographical Sketch of Avi Wigderson.
The authors state that one of their aims was to make the survey accessible to both mathematicians and computer scientists, and this they have achieved admirably. To that I can add that they have produced an expository article that will engage a wide audience: newcomers to the topic will find it accessible, while even the cognoscenti will find something of interest.
Avi Wigderson is a professor at the School of Mathematics, Institute for Advanced Study (IAS), Princeton. He obtained his B.Sc. in computer science from the Technion in 1980 and his Ph.D. from Princeton in 1983. He was a member of the faculty at the Hebrew University in Jerusalem from 1986 to 2003. He joined the permanent faculty of the IAS in 1999. His research interests lie principally in complexity theory, algorithms, randomness, and cryptography. His awards include the Nevanlinna Prize (1994).
3.4. Conant Prize Response of Avi Wigderson.
I am honoured to receive the Conant Prize for my joint paper with Shlomo Hoory and Nati Linial. Many thanks are in order. First and foremost, to Nati and Shlomo for the pleasure of teaching together (at the Hebrew University) the course which resulted in this manuscript and for the big effort of writing it. Thanks to the many students of this course whose scribe notes formed the foundation of that paper. Special thanks to Mark Goresky, who convinced us to write it and whose enthusiasm and meticulous reading of earlier drafts helped get us through the process. Thanks to the many others who read and corrected earlier versions. And finally, thanks to the many colleagues and collaborators from whom I learned so much in the wonderful world of expander graphs.
4.1. The Gödel Prize.
The Gödel Prize for outstanding papers in the area of theoretical computer science is sponsored jointly by the ACM Special Interest Group on Algorithms and Computation Theory (SIGACT). This award is presented annually, with the presentation taking place alternately at the International Colloquium on Automata, Languages, and Programming (ICALP) and ACM Symposium on the Theory of Computing (STOC). The Prize is named in honour of Kurt Gödel in recognition of his major contributions to mathematical logic and of his interest, discovered in a letter he wrote to John von Neumann shortly before Neumann's death, in what has become the famous "P versus NP" question. The Prize includes an award of $5000 (US).
4.2. Institute for Advanced Study Report on the 2009 Gödel Prize.
The 2009 Gödel Prize for outstanding papers in theoretical computer science will be awarded to Avi Wigderson, Herbert A Maass Professor in the School of Mathematics, and former Visitors Omer Reingold (1999-2003) and Salil Vadhan (2000-01). The recipients were selected for their development of a new type of graph product that improves the design of robust computer networks and resolved open questions on error correction and derandomization. The papers cited are "Entropy Waves, the Zig-Zag Graph Product, and New Constant Degree Expanders" by all three (conceived and written at the Institute for Advanced Study) and a subsequent paper, "Undirected Connectivity in Log-Space," by Reingold. The prize is named for Kurt Gödel, who was a Member (1933-34, 1935, 1938, 1940-53) of the Institute and subsequently served on the Faculty (1953-78). The Gödel Prize is awarded jointly by the European Association for Theoretical Computer Science and the Association for Computing Machinery Special Interest Group on Algorithms and Computation Theory and will be presented at the ACM Symposium on the Theory of Computing, held from 31 May to 2 June, in Bethesda, Maryland.
4.3. ACM Special Interest Group on Algorithms and Computation Theory report.
The 2009 Gödel Prize for outstanding papers in the area of theoretical computer science is awarded to
(1) Entropy waves, the zig-zag graph product and new constant degree expanders. Omer Reingold, Salil Vadhan and Avi Wigderson, Annals of Mathematics 155 (2002), 157-187
and
(2) Undirected connectivity in Log-Space. Omer Reingold, Journal of ACM 55 (4) (2007).
Expander graphs, which were introduced by Pinsker in 1973, are constant degree graphs in which each small set of vertices has a large number of outside neighbours. Due to the combination of high connectivity and sparsity (low-degree), these graphs have proved to be of enormous importance to the theory of computation. It is not difficult to see that a random graph is a good expander but as one of the main applications of expanders is to replace randomness by deterministic choices it is crucial to have efficient and deterministic constructions of expanders. Early deterministic explicit constructions of expanders were algebraic in nature, often yielding graphs only of certain sizes with certain degrees.
The first of the two awarded papers gives a completely combinatorial explicit construction of a rich family of expander graphs. The key to the construction is the introduction of the Zig-Zag graph product that makes it possible to iteratively construct large expanders from smaller expanders preserving degree and connectivity. In addition to enabling the construction of expanders, this tool has proved remarkably useful in other contexts as well.
Finally, the set of ideas used in these two papers have already been used to obtain other spectacular results, the most prominent being a new combinatorial proof of the PCP-theorem by Dinur. Other advances are sure to come.
5. The Donald E Knuth Prize (2019).
The Gödel Prize for outstanding papers in the area of theoretical computer science is sponsored jointly by the ACM Special Interest Group on Algorithms and Computation Theory (SIGACT). This award is presented annually, with the presentation taking place alternately at the International Colloquium on Automata, Languages, and Programming (ICALP) and ACM Symposium on the Theory of Computing (STOC). The Prize is named in honour of Kurt Gödel in recognition of his major contributions to mathematical logic and of his interest, discovered in a letter he wrote to John von Neumann shortly before Neumann's death, in what has become the famous "P versus NP" question. The Prize includes an award of $5000 (US).
4.2. Institute for Advanced Study Report on the 2009 Gödel Prize.
The 2009 Gödel Prize for outstanding papers in theoretical computer science will be awarded to Avi Wigderson, Herbert A Maass Professor in the School of Mathematics, and former Visitors Omer Reingold (1999-2003) and Salil Vadhan (2000-01). The recipients were selected for their development of a new type of graph product that improves the design of robust computer networks and resolved open questions on error correction and derandomization. The papers cited are "Entropy Waves, the Zig-Zag Graph Product, and New Constant Degree Expanders" by all three (conceived and written at the Institute for Advanced Study) and a subsequent paper, "Undirected Connectivity in Log-Space," by Reingold. The prize is named for Kurt Gödel, who was a Member (1933-34, 1935, 1938, 1940-53) of the Institute and subsequently served on the Faculty (1953-78). The Gödel Prize is awarded jointly by the European Association for Theoretical Computer Science and the Association for Computing Machinery Special Interest Group on Algorithms and Computation Theory and will be presented at the ACM Symposium on the Theory of Computing, held from 31 May to 2 June, in Bethesda, Maryland.
4.3. ACM Special Interest Group on Algorithms and Computation Theory report.
The 2009 Gödel Prize for outstanding papers in the area of theoretical computer science is awarded to
(1) Entropy waves, the zig-zag graph product and new constant degree expanders. Omer Reingold, Salil Vadhan and Avi Wigderson, Annals of Mathematics 155 (2002), 157-187
and
(2) Undirected connectivity in Log-Space. Omer Reingold, Journal of ACM 55 (4) (2007).
Expander graphs, which were introduced by Pinsker in 1973, are constant degree graphs in which each small set of vertices has a large number of outside neighbours. Due to the combination of high connectivity and sparsity (low-degree), these graphs have proved to be of enormous importance to the theory of computation. It is not difficult to see that a random graph is a good expander but as one of the main applications of expanders is to replace randomness by deterministic choices it is crucial to have efficient and deterministic constructions of expanders. Early deterministic explicit constructions of expanders were algebraic in nature, often yielding graphs only of certain sizes with certain degrees.
The first of the two awarded papers gives a completely combinatorial explicit construction of a rich family of expander graphs. The key to the construction is the introduction of the Zig-Zag graph product that makes it possible to iteratively construct large expanders from smaller expanders preserving degree and connectivity. In addition to enabling the construction of expanders, this tool has proved remarkably useful in other contexts as well.
Finally, the set of ideas used in these two papers have already been used to obtain other spectacular results, the most prominent being a new combinatorial proof of the PCP-theorem by Dinur. Other advances are sure to come.
5.1. Institute of Advanced Study Report.
Avi Wigderson, Herbert H Maass Professor in the School of Mathematics, has been awarded the 2019 Donald E Knuth Prize.
Conferred annually by the ACM Special Interest Group on Algorithms and Computation Theory and the IEEE Technical Committee on the Mathematical Foundations of Computing, the award recognises major research accomplishments and contributions to the foundations of computer science over an extended period of time.
Wigderson is commended specifically for fundamental and lasting contributions in areas including randomised computation, cryptography, circuit complexity, proof complexity, parallel computation, and our understanding of fundamental graph properties. In addition to specific research results in each of these fields, the prize recognises Wigderson's contributions in education and mentoring: his many survey talks and articles (and his new book Mathematics and Computation), and his training of generations of theoretical computer scientists (including over one hundred postdocs in his program at IAS).
5.2. From the report by Sue Gee.
Israeli mathematician and computer scientist, Avi Wigderson, who in addition to much original work in computation and complexity theory, has trained many generations of theoretical computer scientists through his visitor and postdoc program at the Institute for Advanced Study at Princeton, is this year's recipient of the ACM/IEEE Donald E Knuth Prize.
Awarded by the ACM Special Interest Group on Algorithms and Computation Theory, this annual prize of $5,000, established in 1996, comes with a great deal of prestige and anyone in the Theoretical Computer Science community can nominate a candidate. The award is named after Donald Knuth of Stanford University who has been called the "father of the analysis of algorithms" and also dubbed the "Euclid of computer science" and awarded to individuals for contributions to the foundations of computer science.
For 2019, the Knuth Prize committee, chaired by Avrim Blum, selected Avi Wigderson for his work in areas including randomised computation, cryptography, circuit complexity, proof complexity, parallel computation, and the understanding of fundamental graph properties.
5.3. ACM Special Interest Group on Algorithms and Computation Theory Citation.
The 2019 Donald E Knuth Prize will be awarded to Avi Wigderson of the Institute for Advanced Study for fundamental and lasting contributions to the foundations of computer science in areas including randomised computation, cryptography, circuit complexity, proof complexity, parallel computation, and our understanding of fundamental graph properties. Wigderson has also trained many generations of theoretical computer scientists through his visitor and postdoc program at the Institute for Advanced Study.
Wigderson's work revolutionised our understanding of randomness in computation. In a series of results, he showed under widely-believed computational assumptions that every probabilistic polynomial time algorithm can be fully derandomised. In other words, randomness is not necessary for polynomial-time computation. This was achieved by a sequence of papers of his: "Hardness vs. Randomness" with Nisan, "BPP Has Subexponential Time Simulations Unless EXPTIME has Publishable Proofs" with Babai, Fortnow and Nisan, and "P = BPP if E Requires Exponential Circuits: Derandomizing the XOR Lemma" with Impagliazzo. This last result showed that P = BPP is implied by the assumption that there exist functions that can be computed by exponential-time Turing machines that cannot be computed by subexponential-size circuits in the worst case. To this day, the Impagliazzo-Wigderson paper is one of the strongest pieces of evidence we have that P = BPP.
In cryptography, in two landmark papers, one with Goldreich and Micali and one with Ben-Or and Goldwasser, Wigderson showed how one could compute any function securely in the presence of dishonest parties. Wigderson also with Goldreich and Micali showed that all problems with short proofs (i.e., all problems in NP) in fact have zero-knowledge proofs: that is, proofs that yield nothing but their validity, a central cryptographic construct.
Additionally, originating from cryptography but with applications to many areas in theoretical computer science, Wigderson with Ben-Or, Goldwasser, and Kilian defined the model of multiprover interactive proofs. This model for the first time showed how it would be possible for a polynomial-time machine to verify an exponentially-long proof. This idea had substantial impact, and among other things it led to the celebrated PCP theorem and the flow of follow-up works on hardness of approximation.
In the area of parallel computation, Wigderson provided a series of foundational results about parallel computing models. This includes the first RNC algorithm for constructing a perfect matching in a graph with Karp and Upfal, the first NC algorithm for finding a maximal independent set in a graph with Karp, and a number of fundamental lower bound results.
With Reingold, Vadhan and Capalbo, Wigderson gave the first efficient combinatorial constructions of expander graphs, an important class of highly connected sparse graphs. Before this work, only algebraic constructions had been known. Widgerson's development of combinatorial expander constructions enabled a series of important subsequent results including Reingold's deterministic logspace algorithm for st-connectivity.
In addition to specific research results, during his academic career Wigderson has supervised a large number of postdocs and PhD students. He also has written many expository and survey articles, such as the award winning survey "Expander Graphs and their Applications", and he recently published the book "Mathematics and Computation".
6. The Abel Prize (2021).
Avi Wigderson, Herbert H Maass Professor in the School of Mathematics, has been awarded the 2019 Donald E Knuth Prize.
Conferred annually by the ACM Special Interest Group on Algorithms and Computation Theory and the IEEE Technical Committee on the Mathematical Foundations of Computing, the award recognises major research accomplishments and contributions to the foundations of computer science over an extended period of time.
Wigderson is commended specifically for fundamental and lasting contributions in areas including randomised computation, cryptography, circuit complexity, proof complexity, parallel computation, and our understanding of fundamental graph properties. In addition to specific research results in each of these fields, the prize recognises Wigderson's contributions in education and mentoring: his many survey talks and articles (and his new book Mathematics and Computation), and his training of generations of theoretical computer scientists (including over one hundred postdocs in his program at IAS).
5.2. From the report by Sue Gee.
Israeli mathematician and computer scientist, Avi Wigderson, who in addition to much original work in computation and complexity theory, has trained many generations of theoretical computer scientists through his visitor and postdoc program at the Institute for Advanced Study at Princeton, is this year's recipient of the ACM/IEEE Donald E Knuth Prize.
Awarded by the ACM Special Interest Group on Algorithms and Computation Theory, this annual prize of $5,000, established in 1996, comes with a great deal of prestige and anyone in the Theoretical Computer Science community can nominate a candidate. The award is named after Donald Knuth of Stanford University who has been called the "father of the analysis of algorithms" and also dubbed the "Euclid of computer science" and awarded to individuals for contributions to the foundations of computer science.
For 2019, the Knuth Prize committee, chaired by Avrim Blum, selected Avi Wigderson for his work in areas including randomised computation, cryptography, circuit complexity, proof complexity, parallel computation, and the understanding of fundamental graph properties.
5.3. ACM Special Interest Group on Algorithms and Computation Theory Citation.
The 2019 Donald E Knuth Prize will be awarded to Avi Wigderson of the Institute for Advanced Study for fundamental and lasting contributions to the foundations of computer science in areas including randomised computation, cryptography, circuit complexity, proof complexity, parallel computation, and our understanding of fundamental graph properties. Wigderson has also trained many generations of theoretical computer scientists through his visitor and postdoc program at the Institute for Advanced Study.
Wigderson's work revolutionised our understanding of randomness in computation. In a series of results, he showed under widely-believed computational assumptions that every probabilistic polynomial time algorithm can be fully derandomised. In other words, randomness is not necessary for polynomial-time computation. This was achieved by a sequence of papers of his: "Hardness vs. Randomness" with Nisan, "BPP Has Subexponential Time Simulations Unless EXPTIME has Publishable Proofs" with Babai, Fortnow and Nisan, and "P = BPP if E Requires Exponential Circuits: Derandomizing the XOR Lemma" with Impagliazzo. This last result showed that P = BPP is implied by the assumption that there exist functions that can be computed by exponential-time Turing machines that cannot be computed by subexponential-size circuits in the worst case. To this day, the Impagliazzo-Wigderson paper is one of the strongest pieces of evidence we have that P = BPP.
In cryptography, in two landmark papers, one with Goldreich and Micali and one with Ben-Or and Goldwasser, Wigderson showed how one could compute any function securely in the presence of dishonest parties. Wigderson also with Goldreich and Micali showed that all problems with short proofs (i.e., all problems in NP) in fact have zero-knowledge proofs: that is, proofs that yield nothing but their validity, a central cryptographic construct.
Additionally, originating from cryptography but with applications to many areas in theoretical computer science, Wigderson with Ben-Or, Goldwasser, and Kilian defined the model of multiprover interactive proofs. This model for the first time showed how it would be possible for a polynomial-time machine to verify an exponentially-long proof. This idea had substantial impact, and among other things it led to the celebrated PCP theorem and the flow of follow-up works on hardness of approximation.
In the area of parallel computation, Wigderson provided a series of foundational results about parallel computing models. This includes the first RNC algorithm for constructing a perfect matching in a graph with Karp and Upfal, the first NC algorithm for finding a maximal independent set in a graph with Karp, and a number of fundamental lower bound results.
With Reingold, Vadhan and Capalbo, Wigderson gave the first efficient combinatorial constructions of expander graphs, an important class of highly connected sparse graphs. Before this work, only algebraic constructions had been known. Widgerson's development of combinatorial expander constructions enabled a series of important subsequent results including Reingold's deterministic logspace algorithm for st-connectivity.
In addition to specific research results, during his academic career Wigderson has supervised a large number of postdocs and PhD students. He also has written many expository and survey articles, such as the award winning survey "Expander Graphs and their Applications", and he recently published the book "Mathematics and Computation".
6.1. Abel Prize Press Release.
The Norwegian Academy of Science and Letters has decided to award the Abel Prize for 2021 to
László Lovász of Alfréd Rényi Institute of Mathematics (ELKH, MTA Institute of Excellence) and Eötvös Loránd University in Budapest, Hungary, and
Avi Wigderson of the Institute for Advanced Study, Princeton, USA:
"Lovász and Wigderson have been leading forces in this development over the last few decades. Their work interlaces in many ways, and, in particular, they have both made fundamental contributions to understanding randomness in computation and in exploring the boundaries of efficient computation," says Hans Munthe-Kaas, chair of the Abel Committee.
He continues: "Thanks to the ground-breaking work of these two, discrete mathematics and the relatively young field of theoretical computer science are now firmly established as central areas of modern mathematics."
Wigderson is known for his ability to see connections between apparently unrelated areas. He has deepened the connections between mathematics and computer science. He was born in Haifa, Israel, in 1956. His contribution to widening and deepening the field of 'complexity theory' - which concerns itself with the speed and efficiency of algorithms - is arguably greater than that of any single other person.
Wigderson has conducted research into every major open problem in complexity theory. In many ways, the field has evolved around him. He has co-authored papers with more than 100 people and has deepened the connections between mathematics and computer science.
The most important present-day application of complexity theory is internet cryptography. Early in his career, Wigderson made fundamental contributions in this area, including the zero-knowledge proof, which is now used in cryptocurrency technology.
In 1994, Wigderson won the Rolf Nevanlinna Prize for computer science. Among his many other awards are the 2009 Gödel Prize and the 2019 Knuth Prize.
6.2. Abel Prize Citation.
The Norwegian Academy of Science and Letters has decided to award the Abel Prize for 2021 to
László Lovász of Alfréd Rényi Institute of Mathematics (ELKH, MTA Institute of Excellence) and Eötvös Loránd University in Budapest, Hungary, and
Avi Wigderson of the Institute for Advanced Study, Princeton, USA:
Apart from its tremendous impact on broader computer science and practice, TCS provides the foundations of cryptography, and is now having growing influence on several other sciences leading to new insights therein by "employing a computational lens". Discrete structures such as graphs, strings, permutations are central to TCS, and naturally discrete mathematics and TCS have been closely allied fields. While both these fields have bene ted immensely from more traditional areas of mathematics, there has been growing influence in the reverse direction as well. Applications, concepts, and techniques from TCS have motivated new challenges, opened new directions of research, and solved important open problems in pure and applied mathematics.
László Lovász and Avi Wigderson have been leading forces in these developments over the last decades. Their work interlaces in many ways, and, in particular, they have both made fundamental contributions to understanding randomness in computation and in exploring the boundaries of efficient computation.
Avi Wigderson has made broad and profound contributions to all aspects of computational complexity, especially the role of randomness in computation. A randomised algorithm is one that flips coins to compute a solution that is correct with high probability. Over decades, researchers discovered deterministic algorithms for many problems for which only a randomised algorithm was known before. The deterministic algorithm for primality testing, by Agrawal, Kayal and Saxena is a striking example of such a derandomised algorithm. These derandomization results raise the question of whether randomness is ever really essential. In works with László Babai, Lance Fortnow, Noam Nisan and Russell Impagliazzo, Wigderson demonstrated that the answer is likely to be in the negative. Formally, they showed a computational conjecture, similar in spirit to the P ≠ NP conjecture, implies that P = BPP. This means that every randomised algorithm can be derandomised and turned into a deterministic one with comparable efficiency; moreover the derandomisation is generic and universal, without depending on the internal details of the randomised algorithm.
Another way to look at this work is as a trade-off between hardness versus randomness: if there exists a hard enough problem, then randomness can be simulated by efficient deterministic algorithms. Wigderson's subsequent work with Impagliazzo and Valentine Kabanets proves a converse: efficient deterministic algorithms even for specific problems with known randomised algorithms would imply that there must exist such a hard problem.
This work is intimately tied with constructions of pseudorandom (random looking) objects. Wigderson's works have constructed pseudorandom generators that turn a few truly random bits into many pseudorandom bits, extractors that extract nearly perfect random bits from an imperfect source of randomness, Ramsey graphs and expander graphs that are sparse and still have high connectivity. With Omer Reingold and Salil Vadhan, he introduced the zig-zag graph product, giving an elementary method to build expander graphs, and inspiring the combinatorial proof of the PCP Theorem by Irit Dinur and a memory efficient algorithm for the graph connectivity problem by Reingold. The latter gives a method to navigate through a large maze while remembering the identity of only a constant number of intersection points in the maze!
Wigderson's other contributions include zero-knowledge proofs that provide proofs for claims without revealing any extra information besides the claims' validity, and lower bounds on the efficiency of communication protocols, circuits, and formal proof systems.
Thanks to the leadership of Lovász and Wigderson, discrete mathematics and the relatively young field of theoretical computer science are now established as central areas of modern mathematics.
6.3. Abel Prize biography of Avi Wigderson.
When Avi Wigderson began his academic career in the late 1970s, the theory of 'computational complexity' - which concerns itself with the speed and efficiency of algorithms - was in its infancy. Wigderson's contribution to enlarging and deepening the field is arguably greater than that of any single other person, and what was a young subject is now an established field of both mathematics and theoretical computer science. Computational complexity has also become unexpectedly important, providing the theoretical basis for internet security.
Wigderson was born in Haifa, Israel, in 1956. He entered the Technion, the Israeli Institute of Technology, in 1977, and graduated with a B.Sc. in Computer Science in 1980. He moved to Princeton for his graduate studies, receiving his PhD in 1983 for the thesis Studies in Combinatorial Complexity, for which Richard Lipton was his advisor. In 1986 Wigderson returned to Israel to take up a position at the Hebrew University in Jerusalem. He was given tenure the following year and made full professor in 1991.
In the 1970s, computer theoreticians framed certain fundamental ideas about the nature of computation, notably the notions of P and NP. P is the set of problems that computers can solve easily, say, in a few seconds, whereas NP also contains problems that computers find hard to solve, meaning that the known methods can only find the answer in, say, millions of years. The question of whether all these hard problems can be reduced to easy ones, that is, whether or not P = NP, is the foundational question of computational complexity. Indeed, it is now considered one of the most important unsolved questions in all of mathematics.
Wigderson made stunning advances in this area by investigating the role of randomness in aiding computation. Some hard problems can be made easy using algorithms in which the computer flips coins during the computation. If an algorithm relies on coin-flipping, however, there is always a chance that an error can creep into the solution. Wigderson, first together with Noam Nisan, and later with Russell Impagliazzo, showed that for any fast algorithm that can solve a hard problem using coin-flipping, there exists an almost-as-fast algorithm that does not use coin-flipping, provided certain conditions are met.
Wigderson has conducted research into every major open problem in complexity theory. In many ways, the field has grown around him, not only because of his breadth of interests, but also because of his approachable personality and enthusiasm for collaborations. He has co-authored papers with well over 100 people, and has mentored a large number of young complexity theorists. "I consider myself unbelievably lucky to live in this age," he says. "[Computational complexity] is a young field. It is a very democratic field. It is a very friendly field, it is a field that is very collaborative, that suits my nature. And definitely, it is bursting with intellectual problems and challenges."
In 1999 Wigderson joined the Institute for Advanced Study (IAS) in Princeton where he has been ever since. At an event to celebrate Wigderson's sixtieth birthday, in 2016, IAS director Robbert Dijkgraaf said that he had launched a golden age of theoretical computer science at the institute.
Wigderson is known for his ability to see links between apparently unrelated areas. He has deepened the connections between mathematics and computer science. One example is the 'zig-zag graph product', which he developed with Omer Reingold and Salil Vadhan, which links group theory, graph theory and complexity theory, and has surprising applications such as how best to get out of a maze.
The most important present-day application of complexity theory is to cryptography, which is used to secure information on the internet such as credit card numbers and passwords. People who design cryptosystems, for example, must make sure that the task of decoding their system is an NP problem, that is, one that would take computers millions of years to achieve. Early in his career Wigderson made fundamental contributions to a new concept in cryptography, the zero-knowledge proof, which more than 30 years later is now being used in blockchain technology. In a zero-knowledge proof, two people must prove a claim without revealing any knowledge beyond the validity of that claim, such as the example of the two millionaires who want to prove who is richer without either of them letting on how much money they have. Wigderson, together with Oded Goldreich and Silvio Micali, showed that zero-knowledge proofs can be used to prove, in secret, any public result about secret data. Just say, for example, that you want to prove to someone that you have proved a mathematical theorem, but you don't want to reveal any details of how you did it, a zero-knowledge proof will allow you to do this.
In 1994, Wigderson won the Rolf Nevanlinna Prize for computer science, which is awarded by the International Mathematical Union every four years. Among his many other prizes is the 2009 Gödel Prize and the 2019 Knuth Prize.
Wigderson is married to Edna, whom he met at the Technion, and who works in the computer department of the Institute for Advanced Study. They have three children, and two grandchildren.
6.4. Introduction to 'On the works of Avi Wigderson' in 'The Abel Laureates 2018-2022'.
This is an overview of some of the works of Avi Wigderson, 2021 Abel prize laureate. Wigderson's contributions span many fields of computer science and mathematics. In this survey we focus on four subfields: cryptography, pseudorandomness, computational complexity lower bounds, and the theory of optimisation over symmetric manifolds. Even within those fields, we are not able to mention all of Wigderson's results, let alone cover them in full detail. However, we attempt to give a broad view of each field, as well as describe how Wigderson's papers have answered central questions, made key definitions, forged unexpected connections, or otherwise made lasting changes to our ways of thinking in that field.
In a career that has spanned more than 40 years, Wigderson has resolved longstanding open problems, made definitions that shaped entire fields, built unexpected bridges between different areas, and introduced ideas and techniques that inspired generations of researchers. A recurring theme in Wigderson's work has been uncovering the deep connections between computer science and mathematics. His papers have both demonstrated unexpected applications of diverse mathematical areas to questions in computer science, and shown how to use theoretical computer science insights to solve problems in pure mathematics. Many of these beautiful connections are surveyed in Wigderson's own book Mathematics and Computation: A Theory Revolutionizing Technology and Science (Princeton University Press, 2019).
In writing this chapter, we were faced with a daunting task. Wigderson's body of work is so broad and deep that it is impossible to do it justice in a single chapter, or even in a single book. Thus, we chose to focus on a few subfields and, within those, describe only some of Wigderson's central contributions to these fields.
In Section 2 we discuss Wigderson's contribution to cryptography. As we describe there, during the second half of the 20th century, cryptography underwent multiple revolutions. Cryptography transformed from a practical art focused on "secret writing" to a science that protects not only communication but also computation, and provides the underpinning for our digital society. Wigderson's works have been crucial to this revolution, vastly extending its reach through constructions of objects such as zero-knowledge proofs and multi-party secure computation.
In Section 3, we discuss Wigderson's contribution to the field of pseudorandomness. One of the great intellectual achievements of computer science and mathematics alike has been the realisation that many deterministic processes can still behave in "random-like" or pseudorandom manner. Wigderson has led the field in understanding and pursuing the deep implications of pseudorandomness for problems in computational complexity, such as the power of randomized algorithms and circuit lower bounds, and in developing theory and explicit constructions of "pseudorandom objects" like expander graphs and randomness extractors. Wigderson's work in this field used mathematical tools from combinatorics, number theory, algebra, and information theory to answer computer science questions, and has applied computer science abstractions and intuitions to obtain new results in mathematics, such as explicit constructions of Ramsey graphs.
Section 4 covers Wigderson's contribution to the great challenge of theoretical computer science: proving lower bounds on the computational resources needed to achieve computational tasks. Algorithms to solve computational problems have transformed the world and our lives, but for the vast majority of interesting computational tasks, we do not know whether our current algorithms are optimal or whether they can be dramatically improved. To demonstrate optimality, one needs to prove such lower bounds, and this task has turned out to be exceedingly difficult, with the famous P vs. NP question being but one example. While the task is difficult, there has been some progress in it, specifically in proving lower bounds for restricted (but still very useful and interesting) computational models. Wigderson has been a central contributor to this enterprise.
Section 5 covers a line of work by Wigderson and his co-authors on developing and analysing continuous optimisation algorithms for various problems in computational complexity theory, mathematics, and physics. Continuous optimisation is a cornerstone of science and engineering. There is a very successful theory and practice of convex optimisation. However, progress in the area of nonconvex optimization has been hard and sparse, despite a plethora of nonconvex optimisation problems in the area of machine learning. Wigderson and his co-authors, in their attempt to analyse some nonconvex optimisation problems important in complexity theory, realised that these are no ordinary nonconvex problems - nonconvexity arises because the objective function is invariant under certain group actions. This insight led them to synthesise tools from invariant theory, representation theory, and optimisation to develop a quantitative theory of optimisation over Riemannian manifolds that arise from continuous symmetries of noncommutative matrix groups. Moreover, this pursuit revealed connections with and applications to a host of disparate problems in mathematics and physics.
All of us are grateful for having this opportunity to revisit and celebrate Wigderson's work. More than anything, we feel lucky to have had the joy and privilege of knowing Avi as a mentor, colleague, collaborator, and friend.
6.5. Sletsjøe on the 2021 Abel Prize winners.
Proof beyond a reasonable doubt.
To obtain a conviction in court, the prosecution is required to prove its case beyond a reasonable doubt. In mathematics this level of justification is in general not accepted as good enough. A mathematical proof should be deterministic, based on formal logic. The Pythagorean Theorem, stating that the sum of the squares of the two legs of a right-angled triangle equals the square of the hypotenuse, was already proved in the classical antiquity. The proofs (there are many of them) are deterministic since they can be reproduced and will provide the same result every time.
The development of high-speed electronic computers challenged the role of the deterministic proof tradition. It also paved the way for implementing algorithms which were far out of reach to do by hand. The new possibilities opened new questions. What are the limits of computation? How fast can we factorise an integer? Is it possible to verify something by using a probabilistic argument?
In general, it is a very hard task to factorise integers. If you choose a random 1000-digit integer and ask to find the prime decomposition, your computer may find the answer, but it is time-consuming. The sun might have burned out before you reach an answer. On the other hand, if you were given a candidate for the factorisation, it would in fact be an easy task for your computer to verify that the answer is correct. It is much harder to find a needle in the haystack, than verifying that it is in fact the needle you have found. This is the essence of a famous mathematical challenge, the so-called P versus NP problem, one of the seven millennium problems in mathematics.
The Abel Prize Laureates László Lovász and Avi Wigderson have been leading forces in the development of the mathematical foundations for theoretical computer science and its two complementary sub-disciplines: algorithm design and computational complexity. They have both made fundamental contributions to understanding the role of randomness in computation and to exploring the boundaries of efficient computation.
When you visit your bank to make a withdrawal, authentication is a crucial point. The bank must be sure that you are you, either you visit the bank in person or you enter the bank electronically. When you present the bank with your personal code, the bank must be able to verify that you are the true account owner. But, for security reasons, the bank does not want to store your personal code. So is it possible for the bank to verify a code it does not know? The answer is yes, using something called a zero-knowledge proof.
Zero-knowledge proofs were first conceived in 1985 by Shafi Goldwasser, Silvio Micali, and Charles Rackoff. Some years later Oded Goldreich, Silvio Micali, and Abel Prize Laureate Avi Wigderson developed the theory further, creating a zero-knowledge proof system for the graph colouring problem with three colours. This was extremely important, since the existence of this proof guarantees the existence of similar proofs for any problem of the same complexity.
The zero-knowledge proof system for the graph colouring problem with three colours goes as follows: Suppose we have given a separation of a plane into contiguous regions, as is the case of a map. Our task is to colour each country such that no adjacent countries have the same colour. In 1976 Kenneth Appel and Wolfgang Haken gave the first proof for the fact that, regardless of how the countries are located in relation to each other, it is possible to fulfil the colouring task with only four colours. But suppose you only have three different colours. Then in general you will not be able to colour the map. Bolivia and its neighbouring countries is a nice example of this fact. Bolivia has 5 neighbours, Chile, Argentina, Paraguay, Brazil and Peru. The five neighbours surround Bolivia completely.
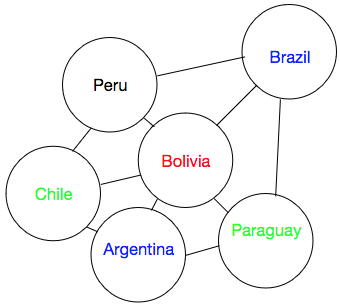
As we see in the illustration, where the connecting lines symbolise common borders, three colours is not enough.
On the contrary, suppose we have a map where it exists a colouring with only three colours. Is it possible for Alice to convince Bob that this is the case, without actually showing Bob the map? Wigderson et al. gave a positive answer; Alice covers the map so that Bob only sees the countries and the borders, but no colours. Bob picks two adjacent countries and asks Alice to uncover the colours. Alice obeys and Bob sees with his own eyes that the colours are different. Alice covers up the colours and Bob picks a new pair of neighbours for his colour check. Again Alice reveals the colours and Bob is satisfied with what he sees. So why does Bob not gain any knowledge from this procedure? The secret is that between two colour revelations Alice permutes the colours randomly. Thus what Bob experiences is that the two adjacent countries have different colour, - which colours is perishable information. After several steps Bob realises that the only possibility that Alice can succeed in every attempt, is that she actually has managed to colour the map with only three colours.
In this way Alice has provided Bob with a zero-knowledge proof. Zero-knowledge proofs are probabilistic, in the sense that the decisive argument for Bob is the overwhelming probability that Alice is right. He accepts Alice's claim, as he finds it proven beyond a reasonable doubt.
Thanks to the leadership of the 2021 Abel Prize Laureates, theoretical computer science has found its place in modern mathematics. The probabilistic approach has proven to be a successful part of the mathematical universe, providing us with fruitful techniques and strategies. Beyond any reasonable doubt it has expanded our mathematical knowledge.
6.6. Post Abel Prize Nieuw Archief interview.
Born in 1956, Avi Wigderson grew up in Haifa, a major port in the North of Israel. He liked playing football and going to the beach with his friends, but already from a young age he developed an interest in solving mathematical problems.
"My father was an engineer who loved puzzles and riddles, and I think he transferred this love to me. His job consisted of fixing electrical problems in engines of ships for the navy. If something would stop working, he would think of it as a puzzle and he would tell me about the different diagnostic tests he would do to locate the problem. He also loved asking me riddles he got from old Russian books, which was infectious at least to me. My two brothers were interested in other things. One is a year younger than me. He was always interested in nature and he ended up as a biologist. My other brother was about six years younger. He was actually interested in engineering, so he liked it when my dad showed us how to fix things. I had no interest in the workings of physical appliances, like a washing machine or a car, but my youngest brother went for it and he became an engineer.
I went to a very good high school, the Hebrew Reali School, it was the only sort of semi-private school in Haifa and it had some very good and inspiring teachers. It also produced some other renowned mathematicians and computer scientists, including Michael Rabin and Noga Alon."
After high school Wigderson wanted to go to University but in Israel you have to go to the army first, which takes at least three years.
"The first year in the army I was in the flying course to be a pilot, but to my great joy I flunked because otherwise I would have had to serve seven years instead of three. The remaining two years I spent in a reasonably interesting office job. Nowadays, with the rise of cybersecurity and cryptography, there are a lot more possibilities to do some intellectually challenging tasks in the army than in my time. Many Israeli researchers in mathematics and computer science that you might have heard of did do interesting things."
After his army service Wigderson returned to his hometown Haifa and there he enrolled in Technion, the Israel institute of technology. Founded in 1912, it is the oldest university of the country and it is sometimes referred to as the MIT of Israel. Despite his early interest in mathematics, he opted for a degree in computer science.
"I was interested in mathematics but my parents, who were Holocaust survivors, thought that I should have a good job. They convinced me to do computer science, where I would learn some maths anyway. I was not from an academic family, so the idea of becoming a university professor was never in the consciousness of our family. I didn't know about this, even when I was in college I didn't realise that my teachers do much more than teaching.
The computer science department was a rather new department. Throughout the country many mathematics departments offered computer science programs already from the sixties, sometimes they were also offered in electrical engineering, but this probably was the first independent computer science department. We were a small class of maybe forty people. Most of our teachers were already researchers who did something in computer science, such as operating systems, programming languages, databases and of course algorithms.
It was not just a theory program, we did a lot of practical things like programming classes, which in these days was still done using punch cards. Sometimes that could be very frustrating: I once wrote a program which consisted of a batch of maybe three hundred punch cards and just before I wanted to put it in the stacker, I dropped it."
During his studies at Technion, Wigderson met his wife Edna, a mathematics student. They got married in their final year of college and after their degree in Israel they wanted to pursue further studies in the United States. Avi ended up doing a PhD in computer science at Princeton, while Edna took a master in mathematics at Rutgers University.
"I applied to about ten universities and I was accepted by Princeton and Yale. My mentor at Technion, Shimon Even, said that Princeton is a nicer place to live, so we went to Princeton. My advisor Dick Lipton was interested in practically everything theoretical. He was interested in cryptography, complexity, algorithms, and in a variety of models of computation. I just followed him and I learned everything he was doing. I also collaborated quite a bit with my other you know classmates from graduate school. I wrote papers with classmates on different subjects and my thesis was just a collection of a few papers. It was not really a cohesive topic but my advisor was happy with it, so I was happy too. In the meantime my wife and I also had our first child, which is maybe a more impressive production than a PhD."
The young family stayed in the United States for three more years but moved to the other side of the country.
"I had three years of postdocs, two of them were in Berkeley and one at the IBM research institute in San Jose. You shouldn't think of IBM just as a company fabricating computers and software. Its research department did real pure theoretical research. At that time, the mid eighties, this institute functioned exactly like any other computer science or math department. There was a lot of freedom: nobody told anybody what to do, the staff members were topnotch theorists: Miklós Ajtai, Ron Fagin, Nicholas Pippenger, Larry Stockmeyer, ... It was a phenomenal place to do a postdoc and I learned a lot there. Needless to say, my two years at Berkeley (one actually at MSRI) were fantastic for my professional development as well."
During that time he also met László Lovász, with whom he would later share the Abel Prize in 2021. The committee awarded the prize: "For their foundational contributions to theoretical computer science and discrete mathematics, and their leading role in shaping them into central fields of modern mathematics."
"Combinatorics, discrete math and computer science are closely related as you know from the Abel prize. I'm very happy to have received the prize together with Laci, not only because it made a lot of sense from a mathematical point of view, but also because he is one of my heroes and a long-time friend. We spent some time in the same places. We were in Berkeley together for a year in the eighties and we were in Princeton for a year in the nineties. During these times we talked a lot and we wrote a couple of papers together."
One of the lines of research that Wigderson pursued in the eighties and nineties was interactive proofs, and in particular the idea of zero-knowledge proofs. This concept formalizes the problem that arises when you want to convince someone that you have a method to do something, without revealing any information about the way it works or giving away the answer to the problem.
"The idea of proving things without providing any knowledge is something paradoxical and therefore very fascinating. I cannot imagine it will not peak anybody's interest once they hear about it. The proposal was made in 1985 by Shafi Goldwasser, Silvio Micali and Charles Rackoff. The motivation they had came from cryptography. It's very natural in cryptographic settings that you would like to do something that depends on a secret, and the other party wants to make sure that you did things correctly without cheating. On the other hand, you don't want to show them how you did it because part of the input is your secret.
The most basic example, one that is done daily millions of times, is when people pick a public key. This often means that you pick two primes, multiply them together and then publish the result. If I give you such a number, why should you believe me that it's a product of two primes? Maybe it's a product of three primes, maybe I didn't do it correctly. How do I convince you? Well I can give you the factors but that would reveal my secret.
That was their question: is it possible for me to convince you that I have a proof of something - and here the proof is the two prime factors - without showing you the proof. Indeed, even without giving you any information whatsoever. For another example: how do I convince you that I have a proof of the Riemann hypothesis without showing you anything that you don't already know."
While the case of the Riemann hypothesis might be out of reach for this article, we can give an example of a zero-knowledge proof inspired by the problem of factoring numbers. Let us assume Peggy (the prover) knows that a number is the product of two big primes and . From basic number theory we know that this means she can invert the function for any which is coprime with by calculating and taking the -th power of . While finding for a given , is not the same task as factoring it is hypothesised to be computationally equivalent. (This is called the RSA assumption.)
Suppose that Peggy wants to convince Victor (the verifier) that she is indeed able to invert without revealing the primes or , she could allow Victor to pick random 's and send her while she returns . If this all reminds you strongly of the RSA algorithm for public key cryptography, this is not a coincidence. (To turn this into a true zero knowledge proof, one has to be a bit more careful to prevent Victor from choosing very specific 's that might reveal some information about .)
"The mid-eighties was a period where there was an explosion in cryptography and the theory of cryptography was full of challenges of this type. There were lots of tasks that people came up with that look impossible to do, like public key encryption, how to sign a document digitally without anybody being able to forge it, or how to exchange a secret in the presence of untrusted parties. Even examples like: how do you play poker over the telephone while still following the rules, were studied. Not only did these challenges come up, but actually it turned out that they were possible in the world of cryptography, once you have a function that is easy to compute but difficult to invert, like multiplication (whose 'inverse' is factoring).
In my opinion the zero-knowledge challenge was maybe the best challenge ever because it seems totally contradictory to any human experience about what convincing is. I mean, how can I convince you of something (which you may not believe) without telling you anything that you don't already know. But it turns out to be not only possible, it's even universal. Everything that is provable at all can be proved in this way. When the idea of zero-knowledge proofs was introduced, everyone was talking about it. It was a big thing because it would be extremely useful for cryptographic protocols, but it was not clear to which extent it was possible.
At that time most of the developments in cryptography were intellectual games. It was just a theory like in normal mathematics: you have some axioms and you're trying to see what you can deduce from them. In this case: which kind of tasks can you perform privately and securely, assuming you have so-called one-way, or trap-door functions, like multiplying integers? The protocols developed for many of these tasks were theoretically efficient but it was not clear that they were directly implementable. Nobody bothered about this and for a good reason: I always believe that practice will follow theory if it's good. It's not that you have to start by taking into consideration every practical detail. Instead you first want to understand the broad picture and develop general techniques before you adapt them to specific situations. Today we all experience the great practical consequences of this theory to electronic commerce, Internet security, et cetera."
In 1986 Wigderson went back to his home country to take up a position at the Hebrew university in Jerusalem at the computer science department. He stayed in Israel for more than a decade before returning to Princeton as a professor at the Institute for Advanced Study, a position he still holds today.
"The computer science department at Hebrew university used to be a part of the mathematics department. The physical separation happened while I was a chair, but even after the split in two, the departments remained very close. Naturally, I had most contact with the combinatorialists such as Nati Linial, Gil Kalai and other computer science theorists. All the courses I taught were open for both mathematics and computer science students, especially the graduate courses. Students of mathematics came to my courses and some of my graduate students actually were math students, so we were one big family."
Just like his teaching and supervising, Wigderson's own research is also on the boundary between mathematics and computer science. A lot of the problems that appear in complexity theory have their origin in abstract mathematics, most of which he did not encounter in his undergraduate studies.
"Most of the advanced math I needed I did not learn in an organised way. I think that's a disadvantage. For a person working in theoretical computer science, especially today, it's much better to get to know lots of basic maths courses in school rather than later on. Since my education was not like that - I just learned the usual basics such as calculus and linear algebra - I had to learn the rest by myself, sometimes from books, sometimes from my colleagues."
Coming from a different field often offers a fresh perspective on the material and allows one to approach problems from a different angle and ask questions that others might overlook or neglect. This can then lead to surprising new results.
"Part of the gut instinct or the DNA of a computer scientist is - not only in math but also in biology and physics - that when you face a theorem or a phenomenon, you want to know what is the process that makes it happen and how efficiently does it do that. Take for example Hilbert's Nullstellensatz. It tells you that if some polynomials do not share a common zero then you can find a linear combination that gives you 1. As a computer scientist you immediately wonder what are these polynomial coefficients, how can I find them efficiently, and what is the complexity of doing this.
This is a fundamental question: an existence theorem of some object is nice but how can I generate it? I think this general question has been extremely fruitful and productive. There are many stories from research that illustrate this."
...
Pure randomness is hard to come by, more often computers are restricted to use variables that look random but in reality are deterministic deep down. Surprisingly, pseudo-number generators based on computational complexity theory can be used to remove randomness from efficient probabilistic algorithms.
"Pseudo-randomness is another theory that I invested a lot of time in. This phenomenon requires a computationally hard function. Take for instance systems of quadratic equations. Nobody has any idea how to solve these efficiently. Even if you work over a finite field, we don't know any algorithm better than exponential time. If you believe that any such natural hard problem requires at least exponential time, then you can eliminate randomness from any efficient probabilistic algorithm. That is another major understanding: that randomness is actually not as powerful as we think it is. Look at all the probabilistic algorithms that people use and that don't seem to have any deterministic counterparts. The truth is they do and this is pretty remarkable.
This realisation happened rather quickly. As a postdoc I wrote a paper with Miklós Ajtai at IBM where we did these kinds of things for a very limited class of algorithms that run very fast in parallel. We already realised that any hard function for this class can serve as a basis for creating pseudo-random generators. This was also known in the cryptographic world, usually under stronger assumptions. Anyway, it was in the air that if you have a hard function you can generate pseudo-randomness from scratch. Then Noam Nisan, a graduate student at Berkeley, came to visit me for a semester at the Hebrew university and together we made this fundamental connection work for any efficient algorithm.
From the beginning, it was obvious to everybody that randomness is powerful, but signs that sometimes you can eliminate them began to crop up. We had all these examples and within a week or a couple of days we realised that it is very general and you can always do it. There were various parameters to make the result much cleaner and stronger. In a sense even though I was not consciously thinking it should be true, we were just pursuing the power of the paradigm that hardness can be converted into randomness."
As illustrated by the examples above, looking at mathematics from a computational perspective can be a very fruitful endeavour and it inspired Wigderson throughout his whole career.
"I think that over forty years my understanding has evolved and improved a lot. Thirty years ago there were some glimpses, not just by me but by the whole community. We didn't understand the full power of this computational lens. Twenty years ago it was much clearer. The algorithmic viewpoint kept improving and I collected many more examples to demonstrate."
In 2019 Wigderson published a book Mathematics and Computation: A Theory Revolutionizing Technology and Science that offered a bird's eye view of computational complexity theory, including all its connections and interactions with mathematics, the natural and social sciences, technology, and philosophy.
"The origin of the book is actually a funny story. I was hoping to write a popular book for the general public. I tried for several years and I didn't get too far. I really had problems with finding the right level of presentation. I didn't realise it was so difficult. I like giving popular lectures and I never had a problem with that, but a book was a different challenge. So then Edna, my wife, suggested that maybe I should write a book I can finish.
I realised that I could finish a book that would be a little more technical but still accessible to the undergrads. I could write something high level, not a book with the proofs but a book about the ideas: the motivations for different parts of computational complexity, the main results and their overall consequences rather than the details.
It would not be a real textbook but it would explain many parts of computational complexity, how they relate to each other and how they connect to math, physics, biology and economics. I am very happy with the way it turned out."
We wholeheartedly agree and recommend it to all our readers, especially those who prefer maths books of a more generalist nature, that do not shy away from the bigger picture.
7. The Turing Award (2023).
The Norwegian Academy of Science and Letters has decided to award the Abel Prize for 2021 to
László Lovász of Alfréd Rényi Institute of Mathematics (ELKH, MTA Institute of Excellence) and Eötvös Loránd University in Budapest, Hungary, and
Avi Wigderson of the Institute for Advanced Study, Princeton, USA:
... for their foundational contributions to theoretical computer science and discrete mathematics, and their leading role in shaping them into central fields of modern mathematics.The theory of 'computational complexity' - which concerns itself with the speed and efficiency of algorithms - first emerged in the 1970s and is now an established field of both mathematics and theoretical computer science. Computational complexity is now a very important field, providing the theoretical basis for internet security. Also in the 1970s, a new generation of mathematicians realised that discrete mathematics had a new area of application in computer science. Today algorithms and internet security applications are an integral part of everyday life for all of us. The work of László Lovász and Avi Wigderson has played an important part in this development.
"Lovász and Wigderson have been leading forces in this development over the last few decades. Their work interlaces in many ways, and, in particular, they have both made fundamental contributions to understanding randomness in computation and in exploring the boundaries of efficient computation," says Hans Munthe-Kaas, chair of the Abel Committee.
He continues: "Thanks to the ground-breaking work of these two, discrete mathematics and the relatively young field of theoretical computer science are now firmly established as central areas of modern mathematics."
Wigderson is known for his ability to see connections between apparently unrelated areas. He has deepened the connections between mathematics and computer science. He was born in Haifa, Israel, in 1956. His contribution to widening and deepening the field of 'complexity theory' - which concerns itself with the speed and efficiency of algorithms - is arguably greater than that of any single other person.
Wigderson has conducted research into every major open problem in complexity theory. In many ways, the field has evolved around him. He has co-authored papers with more than 100 people and has deepened the connections between mathematics and computer science.
The most important present-day application of complexity theory is internet cryptography. Early in his career, Wigderson made fundamental contributions in this area, including the zero-knowledge proof, which is now used in cryptocurrency technology.
In 1994, Wigderson won the Rolf Nevanlinna Prize for computer science. Among his many other awards are the 2009 Gödel Prize and the 2019 Knuth Prize.
6.2. Abel Prize Citation.
The Norwegian Academy of Science and Letters has decided to award the Abel Prize for 2021 to
László Lovász of Alfréd Rényi Institute of Mathematics (ELKH, MTA Institute of Excellence) and Eötvös Loránd University in Budapest, Hungary, and
Avi Wigderson of the Institute for Advanced Study, Princeton, USA:
... for their foundational contributions to theoretical computer science and discrete mathematics, and their leading role in shaping them into central fields of modern mathematics.Theoretical Computer Science (TCS) is the study of the power and limitations of computing. Its roots go back to the foundational works of Kurt Gödel, Alonzo Church, Alan Turing, and John von Neumann, leading to the development of real physical computers. TCS contains two complementary sub-disciplines: algorithm design which develops efficient methods for a multitude of computational problems; and computational complexity, which shows inherent limitations on the efficiency of algorithms. The notion of polynomial-time algorithms put forward in the 1960s by Alan Cobham, Jack Edmonds, and others, and the famous P ≠ NP conjecture of Stephen Cook, Leonid Levin, and Richard Karp had strong impact on the field and on the work of Lovász and Wigderson.
Apart from its tremendous impact on broader computer science and practice, TCS provides the foundations of cryptography, and is now having growing influence on several other sciences leading to new insights therein by "employing a computational lens". Discrete structures such as graphs, strings, permutations are central to TCS, and naturally discrete mathematics and TCS have been closely allied fields. While both these fields have bene ted immensely from more traditional areas of mathematics, there has been growing influence in the reverse direction as well. Applications, concepts, and techniques from TCS have motivated new challenges, opened new directions of research, and solved important open problems in pure and applied mathematics.
László Lovász and Avi Wigderson have been leading forces in these developments over the last decades. Their work interlaces in many ways, and, in particular, they have both made fundamental contributions to understanding randomness in computation and in exploring the boundaries of efficient computation.
Avi Wigderson has made broad and profound contributions to all aspects of computational complexity, especially the role of randomness in computation. A randomised algorithm is one that flips coins to compute a solution that is correct with high probability. Over decades, researchers discovered deterministic algorithms for many problems for which only a randomised algorithm was known before. The deterministic algorithm for primality testing, by Agrawal, Kayal and Saxena is a striking example of such a derandomised algorithm. These derandomization results raise the question of whether randomness is ever really essential. In works with László Babai, Lance Fortnow, Noam Nisan and Russell Impagliazzo, Wigderson demonstrated that the answer is likely to be in the negative. Formally, they showed a computational conjecture, similar in spirit to the P ≠ NP conjecture, implies that P = BPP. This means that every randomised algorithm can be derandomised and turned into a deterministic one with comparable efficiency; moreover the derandomisation is generic and universal, without depending on the internal details of the randomised algorithm.
Another way to look at this work is as a trade-off between hardness versus randomness: if there exists a hard enough problem, then randomness can be simulated by efficient deterministic algorithms. Wigderson's subsequent work with Impagliazzo and Valentine Kabanets proves a converse: efficient deterministic algorithms even for specific problems with known randomised algorithms would imply that there must exist such a hard problem.
This work is intimately tied with constructions of pseudorandom (random looking) objects. Wigderson's works have constructed pseudorandom generators that turn a few truly random bits into many pseudorandom bits, extractors that extract nearly perfect random bits from an imperfect source of randomness, Ramsey graphs and expander graphs that are sparse and still have high connectivity. With Omer Reingold and Salil Vadhan, he introduced the zig-zag graph product, giving an elementary method to build expander graphs, and inspiring the combinatorial proof of the PCP Theorem by Irit Dinur and a memory efficient algorithm for the graph connectivity problem by Reingold. The latter gives a method to navigate through a large maze while remembering the identity of only a constant number of intersection points in the maze!
Wigderson's other contributions include zero-knowledge proofs that provide proofs for claims without revealing any extra information besides the claims' validity, and lower bounds on the efficiency of communication protocols, circuits, and formal proof systems.
Thanks to the leadership of Lovász and Wigderson, discrete mathematics and the relatively young field of theoretical computer science are now established as central areas of modern mathematics.
6.3. Abel Prize biography of Avi Wigderson.
When Avi Wigderson began his academic career in the late 1970s, the theory of 'computational complexity' - which concerns itself with the speed and efficiency of algorithms - was in its infancy. Wigderson's contribution to enlarging and deepening the field is arguably greater than that of any single other person, and what was a young subject is now an established field of both mathematics and theoretical computer science. Computational complexity has also become unexpectedly important, providing the theoretical basis for internet security.
Wigderson was born in Haifa, Israel, in 1956. He entered the Technion, the Israeli Institute of Technology, in 1977, and graduated with a B.Sc. in Computer Science in 1980. He moved to Princeton for his graduate studies, receiving his PhD in 1983 for the thesis Studies in Combinatorial Complexity, for which Richard Lipton was his advisor. In 1986 Wigderson returned to Israel to take up a position at the Hebrew University in Jerusalem. He was given tenure the following year and made full professor in 1991.
In the 1970s, computer theoreticians framed certain fundamental ideas about the nature of computation, notably the notions of P and NP. P is the set of problems that computers can solve easily, say, in a few seconds, whereas NP also contains problems that computers find hard to solve, meaning that the known methods can only find the answer in, say, millions of years. The question of whether all these hard problems can be reduced to easy ones, that is, whether or not P = NP, is the foundational question of computational complexity. Indeed, it is now considered one of the most important unsolved questions in all of mathematics.
Wigderson made stunning advances in this area by investigating the role of randomness in aiding computation. Some hard problems can be made easy using algorithms in which the computer flips coins during the computation. If an algorithm relies on coin-flipping, however, there is always a chance that an error can creep into the solution. Wigderson, first together with Noam Nisan, and later with Russell Impagliazzo, showed that for any fast algorithm that can solve a hard problem using coin-flipping, there exists an almost-as-fast algorithm that does not use coin-flipping, provided certain conditions are met.
Wigderson has conducted research into every major open problem in complexity theory. In many ways, the field has grown around him, not only because of his breadth of interests, but also because of his approachable personality and enthusiasm for collaborations. He has co-authored papers with well over 100 people, and has mentored a large number of young complexity theorists. "I consider myself unbelievably lucky to live in this age," he says. "[Computational complexity] is a young field. It is a very democratic field. It is a very friendly field, it is a field that is very collaborative, that suits my nature. And definitely, it is bursting with intellectual problems and challenges."
In 1999 Wigderson joined the Institute for Advanced Study (IAS) in Princeton where he has been ever since. At an event to celebrate Wigderson's sixtieth birthday, in 2016, IAS director Robbert Dijkgraaf said that he had launched a golden age of theoretical computer science at the institute.
Wigderson is known for his ability to see links between apparently unrelated areas. He has deepened the connections between mathematics and computer science. One example is the 'zig-zag graph product', which he developed with Omer Reingold and Salil Vadhan, which links group theory, graph theory and complexity theory, and has surprising applications such as how best to get out of a maze.
The most important present-day application of complexity theory is to cryptography, which is used to secure information on the internet such as credit card numbers and passwords. People who design cryptosystems, for example, must make sure that the task of decoding their system is an NP problem, that is, one that would take computers millions of years to achieve. Early in his career Wigderson made fundamental contributions to a new concept in cryptography, the zero-knowledge proof, which more than 30 years later is now being used in blockchain technology. In a zero-knowledge proof, two people must prove a claim without revealing any knowledge beyond the validity of that claim, such as the example of the two millionaires who want to prove who is richer without either of them letting on how much money they have. Wigderson, together with Oded Goldreich and Silvio Micali, showed that zero-knowledge proofs can be used to prove, in secret, any public result about secret data. Just say, for example, that you want to prove to someone that you have proved a mathematical theorem, but you don't want to reveal any details of how you did it, a zero-knowledge proof will allow you to do this.
In 1994, Wigderson won the Rolf Nevanlinna Prize for computer science, which is awarded by the International Mathematical Union every four years. Among his many other prizes is the 2009 Gödel Prize and the 2019 Knuth Prize.
Wigderson is married to Edna, whom he met at the Technion, and who works in the computer department of the Institute for Advanced Study. They have three children, and two grandchildren.
6.4. Introduction to 'On the works of Avi Wigderson' in 'The Abel Laureates 2018-2022'.
This is an overview of some of the works of Avi Wigderson, 2021 Abel prize laureate. Wigderson's contributions span many fields of computer science and mathematics. In this survey we focus on four subfields: cryptography, pseudorandomness, computational complexity lower bounds, and the theory of optimisation over symmetric manifolds. Even within those fields, we are not able to mention all of Wigderson's results, let alone cover them in full detail. However, we attempt to give a broad view of each field, as well as describe how Wigderson's papers have answered central questions, made key definitions, forged unexpected connections, or otherwise made lasting changes to our ways of thinking in that field.
In a career that has spanned more than 40 years, Wigderson has resolved longstanding open problems, made definitions that shaped entire fields, built unexpected bridges between different areas, and introduced ideas and techniques that inspired generations of researchers. A recurring theme in Wigderson's work has been uncovering the deep connections between computer science and mathematics. His papers have both demonstrated unexpected applications of diverse mathematical areas to questions in computer science, and shown how to use theoretical computer science insights to solve problems in pure mathematics. Many of these beautiful connections are surveyed in Wigderson's own book Mathematics and Computation: A Theory Revolutionizing Technology and Science (Princeton University Press, 2019).
In writing this chapter, we were faced with a daunting task. Wigderson's body of work is so broad and deep that it is impossible to do it justice in a single chapter, or even in a single book. Thus, we chose to focus on a few subfields and, within those, describe only some of Wigderson's central contributions to these fields.
In Section 2 we discuss Wigderson's contribution to cryptography. As we describe there, during the second half of the 20th century, cryptography underwent multiple revolutions. Cryptography transformed from a practical art focused on "secret writing" to a science that protects not only communication but also computation, and provides the underpinning for our digital society. Wigderson's works have been crucial to this revolution, vastly extending its reach through constructions of objects such as zero-knowledge proofs and multi-party secure computation.
In Section 3, we discuss Wigderson's contribution to the field of pseudorandomness. One of the great intellectual achievements of computer science and mathematics alike has been the realisation that many deterministic processes can still behave in "random-like" or pseudorandom manner. Wigderson has led the field in understanding and pursuing the deep implications of pseudorandomness for problems in computational complexity, such as the power of randomized algorithms and circuit lower bounds, and in developing theory and explicit constructions of "pseudorandom objects" like expander graphs and randomness extractors. Wigderson's work in this field used mathematical tools from combinatorics, number theory, algebra, and information theory to answer computer science questions, and has applied computer science abstractions and intuitions to obtain new results in mathematics, such as explicit constructions of Ramsey graphs.
Section 4 covers Wigderson's contribution to the great challenge of theoretical computer science: proving lower bounds on the computational resources needed to achieve computational tasks. Algorithms to solve computational problems have transformed the world and our lives, but for the vast majority of interesting computational tasks, we do not know whether our current algorithms are optimal or whether they can be dramatically improved. To demonstrate optimality, one needs to prove such lower bounds, and this task has turned out to be exceedingly difficult, with the famous P vs. NP question being but one example. While the task is difficult, there has been some progress in it, specifically in proving lower bounds for restricted (but still very useful and interesting) computational models. Wigderson has been a central contributor to this enterprise.
Section 5 covers a line of work by Wigderson and his co-authors on developing and analysing continuous optimisation algorithms for various problems in computational complexity theory, mathematics, and physics. Continuous optimisation is a cornerstone of science and engineering. There is a very successful theory and practice of convex optimisation. However, progress in the area of nonconvex optimization has been hard and sparse, despite a plethora of nonconvex optimisation problems in the area of machine learning. Wigderson and his co-authors, in their attempt to analyse some nonconvex optimisation problems important in complexity theory, realised that these are no ordinary nonconvex problems - nonconvexity arises because the objective function is invariant under certain group actions. This insight led them to synthesise tools from invariant theory, representation theory, and optimisation to develop a quantitative theory of optimisation over Riemannian manifolds that arise from continuous symmetries of noncommutative matrix groups. Moreover, this pursuit revealed connections with and applications to a host of disparate problems in mathematics and physics.
All of us are grateful for having this opportunity to revisit and celebrate Wigderson's work. More than anything, we feel lucky to have had the joy and privilege of knowing Avi as a mentor, colleague, collaborator, and friend.
6.5. Sletsjøe on the 2021 Abel Prize winners.
Proof beyond a reasonable doubt.
To obtain a conviction in court, the prosecution is required to prove its case beyond a reasonable doubt. In mathematics this level of justification is in general not accepted as good enough. A mathematical proof should be deterministic, based on formal logic. The Pythagorean Theorem, stating that the sum of the squares of the two legs of a right-angled triangle equals the square of the hypotenuse, was already proved in the classical antiquity. The proofs (there are many of them) are deterministic since they can be reproduced and will provide the same result every time.
The development of high-speed electronic computers challenged the role of the deterministic proof tradition. It also paved the way for implementing algorithms which were far out of reach to do by hand. The new possibilities opened new questions. What are the limits of computation? How fast can we factorise an integer? Is it possible to verify something by using a probabilistic argument?
In general, it is a very hard task to factorise integers. If you choose a random 1000-digit integer and ask to find the prime decomposition, your computer may find the answer, but it is time-consuming. The sun might have burned out before you reach an answer. On the other hand, if you were given a candidate for the factorisation, it would in fact be an easy task for your computer to verify that the answer is correct. It is much harder to find a needle in the haystack, than verifying that it is in fact the needle you have found. This is the essence of a famous mathematical challenge, the so-called P versus NP problem, one of the seven millennium problems in mathematics.
The Abel Prize Laureates László Lovász and Avi Wigderson have been leading forces in the development of the mathematical foundations for theoretical computer science and its two complementary sub-disciplines: algorithm design and computational complexity. They have both made fundamental contributions to understanding the role of randomness in computation and to exploring the boundaries of efficient computation.
When you visit your bank to make a withdrawal, authentication is a crucial point. The bank must be sure that you are you, either you visit the bank in person or you enter the bank electronically. When you present the bank with your personal code, the bank must be able to verify that you are the true account owner. But, for security reasons, the bank does not want to store your personal code. So is it possible for the bank to verify a code it does not know? The answer is yes, using something called a zero-knowledge proof.
Zero-knowledge proofs were first conceived in 1985 by Shafi Goldwasser, Silvio Micali, and Charles Rackoff. Some years later Oded Goldreich, Silvio Micali, and Abel Prize Laureate Avi Wigderson developed the theory further, creating a zero-knowledge proof system for the graph colouring problem with three colours. This was extremely important, since the existence of this proof guarantees the existence of similar proofs for any problem of the same complexity.
The zero-knowledge proof system for the graph colouring problem with three colours goes as follows: Suppose we have given a separation of a plane into contiguous regions, as is the case of a map. Our task is to colour each country such that no adjacent countries have the same colour. In 1976 Kenneth Appel and Wolfgang Haken gave the first proof for the fact that, regardless of how the countries are located in relation to each other, it is possible to fulfil the colouring task with only four colours. But suppose you only have three different colours. Then in general you will not be able to colour the map. Bolivia and its neighbouring countries is a nice example of this fact. Bolivia has 5 neighbours, Chile, Argentina, Paraguay, Brazil and Peru. The five neighbours surround Bolivia completely.

As we see in the illustration, where the connecting lines symbolise common borders, three colours is not enough.
On the contrary, suppose we have a map where it exists a colouring with only three colours. Is it possible for Alice to convince Bob that this is the case, without actually showing Bob the map? Wigderson et al. gave a positive answer; Alice covers the map so that Bob only sees the countries and the borders, but no colours. Bob picks two adjacent countries and asks Alice to uncover the colours. Alice obeys and Bob sees with his own eyes that the colours are different. Alice covers up the colours and Bob picks a new pair of neighbours for his colour check. Again Alice reveals the colours and Bob is satisfied with what he sees. So why does Bob not gain any knowledge from this procedure? The secret is that between two colour revelations Alice permutes the colours randomly. Thus what Bob experiences is that the two adjacent countries have different colour, - which colours is perishable information. After several steps Bob realises that the only possibility that Alice can succeed in every attempt, is that she actually has managed to colour the map with only three colours.
In this way Alice has provided Bob with a zero-knowledge proof. Zero-knowledge proofs are probabilistic, in the sense that the decisive argument for Bob is the overwhelming probability that Alice is right. He accepts Alice's claim, as he finds it proven beyond a reasonable doubt.
Thanks to the leadership of the 2021 Abel Prize Laureates, theoretical computer science has found its place in modern mathematics. The probabilistic approach has proven to be a successful part of the mathematical universe, providing us with fruitful techniques and strategies. Beyond any reasonable doubt it has expanded our mathematical knowledge.
6.6. Post Abel Prize Nieuw Archief interview.
Born in 1956, Avi Wigderson grew up in Haifa, a major port in the North of Israel. He liked playing football and going to the beach with his friends, but already from a young age he developed an interest in solving mathematical problems.
"My father was an engineer who loved puzzles and riddles, and I think he transferred this love to me. His job consisted of fixing electrical problems in engines of ships for the navy. If something would stop working, he would think of it as a puzzle and he would tell me about the different diagnostic tests he would do to locate the problem. He also loved asking me riddles he got from old Russian books, which was infectious at least to me. My two brothers were interested in other things. One is a year younger than me. He was always interested in nature and he ended up as a biologist. My other brother was about six years younger. He was actually interested in engineering, so he liked it when my dad showed us how to fix things. I had no interest in the workings of physical appliances, like a washing machine or a car, but my youngest brother went for it and he became an engineer.
I went to a very good high school, the Hebrew Reali School, it was the only sort of semi-private school in Haifa and it had some very good and inspiring teachers. It also produced some other renowned mathematicians and computer scientists, including Michael Rabin and Noga Alon."
After high school Wigderson wanted to go to University but in Israel you have to go to the army first, which takes at least three years.
"The first year in the army I was in the flying course to be a pilot, but to my great joy I flunked because otherwise I would have had to serve seven years instead of three. The remaining two years I spent in a reasonably interesting office job. Nowadays, with the rise of cybersecurity and cryptography, there are a lot more possibilities to do some intellectually challenging tasks in the army than in my time. Many Israeli researchers in mathematics and computer science that you might have heard of did do interesting things."
After his army service Wigderson returned to his hometown Haifa and there he enrolled in Technion, the Israel institute of technology. Founded in 1912, it is the oldest university of the country and it is sometimes referred to as the MIT of Israel. Despite his early interest in mathematics, he opted for a degree in computer science.
"I was interested in mathematics but my parents, who were Holocaust survivors, thought that I should have a good job. They convinced me to do computer science, where I would learn some maths anyway. I was not from an academic family, so the idea of becoming a university professor was never in the consciousness of our family. I didn't know about this, even when I was in college I didn't realise that my teachers do much more than teaching.
The computer science department was a rather new department. Throughout the country many mathematics departments offered computer science programs already from the sixties, sometimes they were also offered in electrical engineering, but this probably was the first independent computer science department. We were a small class of maybe forty people. Most of our teachers were already researchers who did something in computer science, such as operating systems, programming languages, databases and of course algorithms.
It was not just a theory program, we did a lot of practical things like programming classes, which in these days was still done using punch cards. Sometimes that could be very frustrating: I once wrote a program which consisted of a batch of maybe three hundred punch cards and just before I wanted to put it in the stacker, I dropped it."
During his studies at Technion, Wigderson met his wife Edna, a mathematics student. They got married in their final year of college and after their degree in Israel they wanted to pursue further studies in the United States. Avi ended up doing a PhD in computer science at Princeton, while Edna took a master in mathematics at Rutgers University.
"I applied to about ten universities and I was accepted by Princeton and Yale. My mentor at Technion, Shimon Even, said that Princeton is a nicer place to live, so we went to Princeton. My advisor Dick Lipton was interested in practically everything theoretical. He was interested in cryptography, complexity, algorithms, and in a variety of models of computation. I just followed him and I learned everything he was doing. I also collaborated quite a bit with my other you know classmates from graduate school. I wrote papers with classmates on different subjects and my thesis was just a collection of a few papers. It was not really a cohesive topic but my advisor was happy with it, so I was happy too. In the meantime my wife and I also had our first child, which is maybe a more impressive production than a PhD."
The young family stayed in the United States for three more years but moved to the other side of the country.
"I had three years of postdocs, two of them were in Berkeley and one at the IBM research institute in San Jose. You shouldn't think of IBM just as a company fabricating computers and software. Its research department did real pure theoretical research. At that time, the mid eighties, this institute functioned exactly like any other computer science or math department. There was a lot of freedom: nobody told anybody what to do, the staff members were topnotch theorists: Miklós Ajtai, Ron Fagin, Nicholas Pippenger, Larry Stockmeyer, ... It was a phenomenal place to do a postdoc and I learned a lot there. Needless to say, my two years at Berkeley (one actually at MSRI) were fantastic for my professional development as well."
During that time he also met László Lovász, with whom he would later share the Abel Prize in 2021. The committee awarded the prize: "For their foundational contributions to theoretical computer science and discrete mathematics, and their leading role in shaping them into central fields of modern mathematics."
"Combinatorics, discrete math and computer science are closely related as you know from the Abel prize. I'm very happy to have received the prize together with Laci, not only because it made a lot of sense from a mathematical point of view, but also because he is one of my heroes and a long-time friend. We spent some time in the same places. We were in Berkeley together for a year in the eighties and we were in Princeton for a year in the nineties. During these times we talked a lot and we wrote a couple of papers together."
One of the lines of research that Wigderson pursued in the eighties and nineties was interactive proofs, and in particular the idea of zero-knowledge proofs. This concept formalizes the problem that arises when you want to convince someone that you have a method to do something, without revealing any information about the way it works or giving away the answer to the problem.
"The idea of proving things without providing any knowledge is something paradoxical and therefore very fascinating. I cannot imagine it will not peak anybody's interest once they hear about it. The proposal was made in 1985 by Shafi Goldwasser, Silvio Micali and Charles Rackoff. The motivation they had came from cryptography. It's very natural in cryptographic settings that you would like to do something that depends on a secret, and the other party wants to make sure that you did things correctly without cheating. On the other hand, you don't want to show them how you did it because part of the input is your secret.
The most basic example, one that is done daily millions of times, is when people pick a public key. This often means that you pick two primes, multiply them together and then publish the result. If I give you such a number, why should you believe me that it's a product of two primes? Maybe it's a product of three primes, maybe I didn't do it correctly. How do I convince you? Well I can give you the factors but that would reveal my secret.
That was their question: is it possible for me to convince you that I have a proof of something - and here the proof is the two prime factors - without showing you the proof. Indeed, even without giving you any information whatsoever. For another example: how do I convince you that I have a proof of the Riemann hypothesis without showing you anything that you don't already know."
While the case of the Riemann hypothesis might be out of reach for this article, we can give an example of a zero-knowledge proof inspired by the problem of factoring numbers. Let us assume Peggy (the prover) knows that a number is the product of two big primes and . From basic number theory we know that this means she can invert the function for any which is coprime with by calculating and taking the -th power of . While finding for a given , is not the same task as factoring it is hypothesised to be computationally equivalent. (This is called the RSA assumption.)
Suppose that Peggy wants to convince Victor (the verifier) that she is indeed able to invert without revealing the primes or , she could allow Victor to pick random 's and send her while she returns . If this all reminds you strongly of the RSA algorithm for public key cryptography, this is not a coincidence. (To turn this into a true zero knowledge proof, one has to be a bit more careful to prevent Victor from choosing very specific 's that might reveal some information about .)
"The mid-eighties was a period where there was an explosion in cryptography and the theory of cryptography was full of challenges of this type. There were lots of tasks that people came up with that look impossible to do, like public key encryption, how to sign a document digitally without anybody being able to forge it, or how to exchange a secret in the presence of untrusted parties. Even examples like: how do you play poker over the telephone while still following the rules, were studied. Not only did these challenges come up, but actually it turned out that they were possible in the world of cryptography, once you have a function that is easy to compute but difficult to invert, like multiplication (whose 'inverse' is factoring).
In my opinion the zero-knowledge challenge was maybe the best challenge ever because it seems totally contradictory to any human experience about what convincing is. I mean, how can I convince you of something (which you may not believe) without telling you anything that you don't already know. But it turns out to be not only possible, it's even universal. Everything that is provable at all can be proved in this way. When the idea of zero-knowledge proofs was introduced, everyone was talking about it. It was a big thing because it would be extremely useful for cryptographic protocols, but it was not clear to which extent it was possible.
At that time most of the developments in cryptography were intellectual games. It was just a theory like in normal mathematics: you have some axioms and you're trying to see what you can deduce from them. In this case: which kind of tasks can you perform privately and securely, assuming you have so-called one-way, or trap-door functions, like multiplying integers? The protocols developed for many of these tasks were theoretically efficient but it was not clear that they were directly implementable. Nobody bothered about this and for a good reason: I always believe that practice will follow theory if it's good. It's not that you have to start by taking into consideration every practical detail. Instead you first want to understand the broad picture and develop general techniques before you adapt them to specific situations. Today we all experience the great practical consequences of this theory to electronic commerce, Internet security, et cetera."
In 1986 Wigderson went back to his home country to take up a position at the Hebrew university in Jerusalem at the computer science department. He stayed in Israel for more than a decade before returning to Princeton as a professor at the Institute for Advanced Study, a position he still holds today.
"The computer science department at Hebrew university used to be a part of the mathematics department. The physical separation happened while I was a chair, but even after the split in two, the departments remained very close. Naturally, I had most contact with the combinatorialists such as Nati Linial, Gil Kalai and other computer science theorists. All the courses I taught were open for both mathematics and computer science students, especially the graduate courses. Students of mathematics came to my courses and some of my graduate students actually were math students, so we were one big family."
Just like his teaching and supervising, Wigderson's own research is also on the boundary between mathematics and computer science. A lot of the problems that appear in complexity theory have their origin in abstract mathematics, most of which he did not encounter in his undergraduate studies.
"Most of the advanced math I needed I did not learn in an organised way. I think that's a disadvantage. For a person working in theoretical computer science, especially today, it's much better to get to know lots of basic maths courses in school rather than later on. Since my education was not like that - I just learned the usual basics such as calculus and linear algebra - I had to learn the rest by myself, sometimes from books, sometimes from my colleagues."
Coming from a different field often offers a fresh perspective on the material and allows one to approach problems from a different angle and ask questions that others might overlook or neglect. This can then lead to surprising new results.
"Part of the gut instinct or the DNA of a computer scientist is - not only in math but also in biology and physics - that when you face a theorem or a phenomenon, you want to know what is the process that makes it happen and how efficiently does it do that. Take for example Hilbert's Nullstellensatz. It tells you that if some polynomials do not share a common zero then you can find a linear combination that gives you 1. As a computer scientist you immediately wonder what are these polynomial coefficients, how can I find them efficiently, and what is the complexity of doing this.
This is a fundamental question: an existence theorem of some object is nice but how can I generate it? I think this general question has been extremely fruitful and productive. There are many stories from research that illustrate this."
...
Pure randomness is hard to come by, more often computers are restricted to use variables that look random but in reality are deterministic deep down. Surprisingly, pseudo-number generators based on computational complexity theory can be used to remove randomness from efficient probabilistic algorithms.
"Pseudo-randomness is another theory that I invested a lot of time in. This phenomenon requires a computationally hard function. Take for instance systems of quadratic equations. Nobody has any idea how to solve these efficiently. Even if you work over a finite field, we don't know any algorithm better than exponential time. If you believe that any such natural hard problem requires at least exponential time, then you can eliminate randomness from any efficient probabilistic algorithm. That is another major understanding: that randomness is actually not as powerful as we think it is. Look at all the probabilistic algorithms that people use and that don't seem to have any deterministic counterparts. The truth is they do and this is pretty remarkable.
This realisation happened rather quickly. As a postdoc I wrote a paper with Miklós Ajtai at IBM where we did these kinds of things for a very limited class of algorithms that run very fast in parallel. We already realised that any hard function for this class can serve as a basis for creating pseudo-random generators. This was also known in the cryptographic world, usually under stronger assumptions. Anyway, it was in the air that if you have a hard function you can generate pseudo-randomness from scratch. Then Noam Nisan, a graduate student at Berkeley, came to visit me for a semester at the Hebrew university and together we made this fundamental connection work for any efficient algorithm.
From the beginning, it was obvious to everybody that randomness is powerful, but signs that sometimes you can eliminate them began to crop up. We had all these examples and within a week or a couple of days we realised that it is very general and you can always do it. There were various parameters to make the result much cleaner and stronger. In a sense even though I was not consciously thinking it should be true, we were just pursuing the power of the paradigm that hardness can be converted into randomness."
As illustrated by the examples above, looking at mathematics from a computational perspective can be a very fruitful endeavour and it inspired Wigderson throughout his whole career.
"I think that over forty years my understanding has evolved and improved a lot. Thirty years ago there were some glimpses, not just by me but by the whole community. We didn't understand the full power of this computational lens. Twenty years ago it was much clearer. The algorithmic viewpoint kept improving and I collected many more examples to demonstrate."
In 2019 Wigderson published a book Mathematics and Computation: A Theory Revolutionizing Technology and Science that offered a bird's eye view of computational complexity theory, including all its connections and interactions with mathematics, the natural and social sciences, technology, and philosophy.
"The origin of the book is actually a funny story. I was hoping to write a popular book for the general public. I tried for several years and I didn't get too far. I really had problems with finding the right level of presentation. I didn't realise it was so difficult. I like giving popular lectures and I never had a problem with that, but a book was a different challenge. So then Edna, my wife, suggested that maybe I should write a book I can finish.
I realised that I could finish a book that would be a little more technical but still accessible to the undergrads. I could write something high level, not a book with the proofs but a book about the ideas: the motivations for different parts of computational complexity, the main results and their overall consequences rather than the details.
It would not be a real textbook but it would explain many parts of computational complexity, how they relate to each other and how they connect to math, physics, biology and economics. I am very happy with the way it turned out."
We wholeheartedly agree and recommend it to all our readers, especially those who prefer maths books of a more generalist nature, that do not shy away from the bigger picture.
7.1. Turing Award Press Release.
Avi Wigderson, Herbert H Maass Professor in the Institute for Advanced Study's School of Mathematics, was named by the Association for Computing Machinery (ACM) as the recipient of the 2023 ACM A.M. Turing Award, often referred to as the "Nobel Prize of Computing." With this honour, Wigderson has become the first person to receive both a Turing Award and the Abel Prize, widely considered to be the highest recognition for lifetime achievement in mathematics.
The Turing award recognizes Wigderson's foundational contributions to the theory of computation, which include reshaping understanding of the role of randomness in computation, and decades of intellectual leadership in theoretical computer science.
"I am excited that the ACM has again recognised with this award the theory of computation community, which has contributed so much to computing practice and technology," said Wigderson. "I feel lucky to be part of this extremely dynamic community, whose fundamental goals have deep conceptual, intellectual, and scientific meaning, well beyond practical motivations. My four decades in this field have been a continuous joyride, with fun problems, brilliant researchers, and many students, postdocs, and collaborators who have become close friends." An invitation to the important field and its many parts is available in Wigderson's book Mathematics and Computation, which is freely available from his website.
At IAS, Wigderson leads a program in Computer Science and Discrete Mathematics (CSDM), which was formally established in 1999 with his appointment to the permanent Faculty. However, the Institute's history as a leading center for computational research stretches back far beyond this. The Electronic Computer Project (ECP), led by founding IAS Faculty John von Neumann, resulted in the construction of one of the world's first stored-program computers on the Institute's campus. The computer produced by the ECP was the practical realization of the mathematical foundations of computing articulated by British mathematician Alan M Turing, after whom the ACM A M Turing Award is named. Von Neumann has also made many theoretical contributions to understanding computation in cellular automata, fault-tolerant circuits, and the brain.
"Ever since von Neumann's IAS computer project turned Turing's theoretical computational model into a reality that launched the computing revolution, theorists following their curiosity and mathematical insights have paved the way for the new computing technologies we all use," said David Nirenberg, IAS Director and Leon Levy Professor. "Avi has continued that tradition at the Institute for the past quarter century, and I am delighted to congratulate him on the 2023 ACM A M Turing Award, which recognizes his many contributions to the theoretical foundations of computer science."
Wigderson's key contributions have enhanced understanding of the role of randomness and pseudorandomness in computation. Computer scientists have discovered a remarkable connection between randomness and computational difficulty (i.e., identifying natural problems that have no efficient algorithms). Working with colleagues, Wigderson authored a highly influential series of works on trading hardness for randomness. They proved, under standard and widely believed computational assumptions, that every probabilistic polynomial time algorithm can be efficiently derandomized (namely, made fully deterministic). In other words, randomness is not necessary for efficient computation. This sequence of works revolutionized the ways in which computer scientists think about randomness, ideas which were applicable to many areas of theoretical computer science.
"Avi has made fundamental contributions to the theory of computation from parallel algorithms to cryptography to absolutely all aspects of complexity theory," said Shafi Goldwasser, Director of the Simons Institute for the Theory of Computing, a past IAS Visiting Professor (2021), and a 2012 A M Turing Award Laureate. "His numerous contributions over decades to the areas of derandomization and pseudorandomness has led us to a deep understanding of the deep role of randomness in computing."
In addition to these groundbreaking technical contributions, Wigderson is recognized as an esteemed mentor and colleague, who has advised countless young researchers.
Prior to joining the IAS Faculty, Wigderson held academic appointments at the University of California, Berkeley (1983–84); IBM Research, San Jose (1984–85); Mathematical Sciences Research Institute, Berkeley (1985–86); Princeton University (1990–92); and the Hebrew University of Jerusalem (1986–2003).
Wigderson is the recipient of numerous other awards, including the Rolf Nevanlinna Prize (1994); Levi L Conant Prize (2008); Gödel Prize (2009); Donald E Knuth Prize (2019); Abel Prize (2021); and Edsger W Dijkstra Prize in Distributed Computing (2023). He is currently a Fellow of the ACM (since 2018) and a member of the American Academy of Arts and Sciences (since 2011) and the National Academy of Sciences (since 2013).
Avi Wigderson, Herbert H Maass Professor in the Institute for Advanced Study's School of Mathematics, was named by the Association for Computing Machinery (ACM) as the recipient of the 2023 ACM A.M. Turing Award, often referred to as the "Nobel Prize of Computing." With this honour, Wigderson has become the first person to receive both a Turing Award and the Abel Prize, widely considered to be the highest recognition for lifetime achievement in mathematics.
The Turing award recognizes Wigderson's foundational contributions to the theory of computation, which include reshaping understanding of the role of randomness in computation, and decades of intellectual leadership in theoretical computer science.
"I am excited that the ACM has again recognised with this award the theory of computation community, which has contributed so much to computing practice and technology," said Wigderson. "I feel lucky to be part of this extremely dynamic community, whose fundamental goals have deep conceptual, intellectual, and scientific meaning, well beyond practical motivations. My four decades in this field have been a continuous joyride, with fun problems, brilliant researchers, and many students, postdocs, and collaborators who have become close friends." An invitation to the important field and its many parts is available in Wigderson's book Mathematics and Computation, which is freely available from his website.
At IAS, Wigderson leads a program in Computer Science and Discrete Mathematics (CSDM), which was formally established in 1999 with his appointment to the permanent Faculty. However, the Institute's history as a leading center for computational research stretches back far beyond this. The Electronic Computer Project (ECP), led by founding IAS Faculty John von Neumann, resulted in the construction of one of the world's first stored-program computers on the Institute's campus. The computer produced by the ECP was the practical realization of the mathematical foundations of computing articulated by British mathematician Alan M Turing, after whom the ACM A M Turing Award is named. Von Neumann has also made many theoretical contributions to understanding computation in cellular automata, fault-tolerant circuits, and the brain.
"Ever since von Neumann's IAS computer project turned Turing's theoretical computational model into a reality that launched the computing revolution, theorists following their curiosity and mathematical insights have paved the way for the new computing technologies we all use," said David Nirenberg, IAS Director and Leon Levy Professor. "Avi has continued that tradition at the Institute for the past quarter century, and I am delighted to congratulate him on the 2023 ACM A M Turing Award, which recognizes his many contributions to the theoretical foundations of computer science."
Wigderson's key contributions have enhanced understanding of the role of randomness and pseudorandomness in computation. Computer scientists have discovered a remarkable connection between randomness and computational difficulty (i.e., identifying natural problems that have no efficient algorithms). Working with colleagues, Wigderson authored a highly influential series of works on trading hardness for randomness. They proved, under standard and widely believed computational assumptions, that every probabilistic polynomial time algorithm can be efficiently derandomized (namely, made fully deterministic). In other words, randomness is not necessary for efficient computation. This sequence of works revolutionized the ways in which computer scientists think about randomness, ideas which were applicable to many areas of theoretical computer science.
"Avi has made fundamental contributions to the theory of computation from parallel algorithms to cryptography to absolutely all aspects of complexity theory," said Shafi Goldwasser, Director of the Simons Institute for the Theory of Computing, a past IAS Visiting Professor (2021), and a 2012 A M Turing Award Laureate. "His numerous contributions over decades to the areas of derandomization and pseudorandomness has led us to a deep understanding of the deep role of randomness in computing."
In addition to these groundbreaking technical contributions, Wigderson is recognized as an esteemed mentor and colleague, who has advised countless young researchers.
Prior to joining the IAS Faculty, Wigderson held academic appointments at the University of California, Berkeley (1983–84); IBM Research, San Jose (1984–85); Mathematical Sciences Research Institute, Berkeley (1985–86); Princeton University (1990–92); and the Hebrew University of Jerusalem (1986–2003).
Wigderson is the recipient of numerous other awards, including the Rolf Nevanlinna Prize (1994); Levi L Conant Prize (2008); Gödel Prize (2009); Donald E Knuth Prize (2019); Abel Prize (2021); and Edsger W Dijkstra Prize in Distributed Computing (2023). He is currently a Fellow of the ACM (since 2018) and a member of the American Academy of Arts and Sciences (since 2011) and the National Academy of Sciences (since 2013).
Last Updated April 2024