V Ya Zinger addresses the Moscow Mathematical Society in 1869
The following talk was delivered at the annual meeting of the Moscow Mathematical Society on 19 February 1869 by Vasily Yakovlevich Zinger. It was published as V Ya Zinger, On the fundamental theorem of higher geometry, Mathematicheskii Sbornik 4 (1) (1869), 23-36. The Society was founded in 1864 and Zinger was addressing it when it was five years old. The president of the Society at this time was August Yulevich Davidov, who had been elected as the second president following the death of Nikolai Dmetrievich Brashman in 1866. Zinger was vice-president when he delivered his lecture and would become the third president in 1886.
On the fundamental theorem of higher geometry, by V Ya Zinger.
From the interests and hopes of the Moscow Mathematical Society our thoughts naturally turn to the most important interests and great hopes of modern science. The aims of our Society are closely connected with the modern problems of the mathematical sciences and, recalling here the results of the still very recent activity of the Society, we are pleased to think that its works not only express a useful striving for the development and dissemination of mathematical knowledge in our fatherland, but are also of significance for science itself.
At this first celebration of the first mathematical society in Russia, I have the flattering duty of engaging your gracious attention with a conversation of scientific content. I have decided to choose for this purpose a subject related to higher geometry, because this science is of special interest and deserves attention in many respects. Higher geometry, unfortunately still very little widespread, especially among us, is one of the sciences that has arisen and developed only in recent times: it is also called new geometry; and yet, both in content and in its fundamental principles, and especially in its method, it stands closer than all other sciences to the geometry of the ancients. The science which is the highest in importance and depth of its further investigations, it begins with the most elementary principles and in this sense represents, as it were, a direct continuation of elementary geometry. The history of mathematics over the last half century shows us that the rise of higher geometry had an important significance for other branches of mathematics; this is especially clearly seen in analytical geometry, which was completely transformed under the influence of the new science. Finally, the development of higher geometry represents one of the clearest signs of the revolution which is now taking place in the field of mathematical sciences and which has become sufficiently clear in our time, thanks to many indisputable facts; I am talking about the desire of the direct, immediate method of research to take its proper place alongside the so-called analytical method, which for about two centuries had a decisive predominance in science.
I intend at this moment, without going into unnecessary details, to say a few words about the historical origin and the important significance of the theorem which serves as the basis of advanced geometry.
In the early days after the revival of science in Europe, almost the only sources and guides for the study of mathematics were the monuments preserved from the brilliant, but very distant, era of ancient Greek science. It is clear that in this first period of development, the methods of the ancients should have predominated in mathematical research both in spirit and form. Pascal, Descartes, Leibniz and Newton, like the ancients, were at the same time geometers and philosophers, and their works still bear the imprint of the ancient spirit. On new soil and under new conditions, the renewed reason of man laid claim to new rights; The desire for abstraction and generalisation, little characteristic of the ancient world, showed the exact sciences completely new paths. The general method of studying curved lines - the method of coordinates - discovered by Descartes, naturally led to a general method of drawing tangents, i.e., to the discovery of the calculus of infinitesimals. The ideas of Leibniz and Newton were destined to completely change the character of mathematics and for a long time to captivate all minds in new areas of research. Indeed, the entire vast material of modern mathematics was developed under the influence of the enormous impulse communicated to science by the discoveries of Newton and Leibniz. Algebraic analysis and differential calculus appeared in all their power, and everyone's efforts were directed towards developing, with the help of these new tools, a countless number of newly revived questions and theories.
But every method of investigation, however general and powerful, necessarily has only a limited sphere of application, outside of which it is either completely powerless, or must yield priority to other methods more proper to the subject under study. The chief defect of algebraic analysis as a scientific instrument is that between the formulation of the question and the result obtained it introduces a more or less long series of operations, performed by us without any relation to the question itself; because of this the results very often suffer from a lack of clarity and simplicity, and sometimes cannot be interpreted at all. Who does not know such examples even among the problems of elementary geometry? Sometimes the most intricate problem, the immediate geometric solution of which does not present anything difficult or obscure, is solved with extreme complexity by analytical methods, and after this, to explain the solution obtained is sometimes even more difficult than to find it. In general, analysis, irreplaceable by anything in its own sphere, loses its advantages in solving questions in which quantitative relations are of secondary interest, in application to visual objects, all the details of which are clearly distinguished by our mind; in such cases, generalisations are for the most part obvious, so that here algebraic analysis in all respects must give way to such methods as lead to the result by direct reasoning about the essence of the object. The ancient geometers used almost exclusively this direct method of investigation, which has its precious qualities: clarity, brevity, and the ability to satisfy the inquisitiveness of our minds with particular completeness. At present, this method has been enriched with new views and has acquired greater power and extraordinary elegance; It is mainly applied to geometric questions, but there are also many numerical questions, questions of physics and mechanics, which are resolved with particular clarity and convenience in a direct way, even without any mediation of algebra.
At the beginning of the present century a reaction is manifested against the exclusive dominance of algebra as a tool, applied indifferently in all cases. Monge creates descriptive geometry, Carnot in Geometrie de positions rebels against the shortcomings of analytical methods and gives his theory of transversals; In 1813, a young engineer of Napoleon's army, Poncelet, captured by the Russians in Saratov, discovered in the simple idea of perspective a source of new and profound geometrical considerations, which later served as the basis for his extensive research on the projective properties of figures.
Somewhat later than that time, a young French scientist, currently one of the oldest members of the Paris Academy, Chasles, was studying the geometry of the ancients: he was preparing his famous work on the historical development of geometrical methods. Acquaintance with the history of ancient science drew his attention to one fact that had previously interested many scientists.
It is known that many of the works of the ancient geometers have not reached us and are known to us only through the indications and commentaries of other writers, especially through the commentaries of Pappus, a geometer of the fourth century AD. Those of these monuments about which sufficient indications have been preserved were restored in the spirit of ancient geometry by scholars of the seventeenth and eighteenth centuries. Among the lost works is Euclid's book "Porisms"; this book has always aroused special interest in mathematicians, because Pappus speaks of it as the most profound work of Euclid and ascribes to it extraordinary importance. The three books of Porisms, according to Pappus, contained 171 porisms (special kinds of theorems); of these he gives only one, and divides all the others into 29 kinds; to facilitate the study of the "Porisms" he adds 38 lemmas of his own. But the obscurity and incompleteness of the preserved text and the loss of the drawings were the reason that the content and character of this work, the very meaning of the theorem given by Pappus, and especially the importance that was attributed to the "Porisms" in antiquity - all this remained a riddle for a long time. The famous astronomer Halley, one of the most profound experts in ancient geometry, who restored several lost monuments of antiquity, confessed that he understood nothing in Pappus's text on Euclid's porisms. Robert Simson in 1723 finally succeeded in explaining the meaning of the theorem, which is given in full by Pappus, and in finding 10 propositions that fit some of the genera indicated by Pappus. After this, many scientists, almost without ceasing, tried to explain this riddle, bequeathed to us by the ancient world. Chasles decided to direct his efforts to the same goal. But at the very beginning he turned his attention to a theorem, located between Pappus's lemmas on "Porisms" and found in another place in the same writer. This simple theorem gave a completely different direction to Chasles' activity and distracted him for a long time from his original goal, which he nevertheless accomplished, although much later (his work on "Euclid's Porisms" was published only in 1860). Chasles noticed that this one theorem includes the initial principles of all the geometric methods known to date: the principles of correspondence and reciprocity, the methods of projections, transformations of figures and transversals. Thus, from one fundamental theorem there soon developed a whole extensive science, which Chasles called higher geometry; he first gave a course on this science in Paris in 1847 and published its principles with an application to rectilinear figures and the circle in 1852 (Traite de Geometrie superieure).
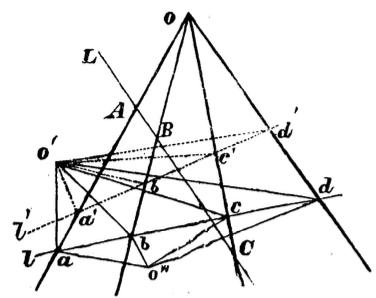
Let us now turn to the theorem itself. Let us imagine four lines on a plane passing through the same point 0; any line in general will intersect these four lines at four points ; the theorem consists in the fact that the quotient of two ratios and , or, what is the same, the ratio of rectangles , remains constant for any position of the secant. Indeed, expressing the segments included in this ratio from the corresponding triangles through the sines of the opposite angles, or determining the areas of these triangles in a two-way manner, we immediately find:
Since the second part depends only on the relative position of the four straight lines intersecting at O, the first part has a constant value, whatever the position of its secant. On the other hand, we see that if we leave the first part unchanged, then the second must also remain constant, i.e., if we connect the ranges of points , or with the help of straight lines with any points of the plane, ... for the angles formed at each of these points, the expression
will always have the same value.
This theorem obviously applies to every four points of a straight line, and to every four corresponding straight lines passing through . Let us agree to call the sequence of all points lying on one straight line a range of points; and the sequence of all straight lines passing through one point a pencil of rays; let us also call the expression which constitutes the first part of our theorem a complex ratio of four points of a range, and the second part a complex ratio of four rays of a pencil, then we can express this theorem in the following words: the complex ratio of four points of a range is always equal to the complex ratio of four corresponding rays of a pencil. A range and a pencil represent, according to Steiner, two simplest geometric images, and the fundamental theorem of higher geometry represents the relationship between the elements of these simplest geometric images when they are in correspondence (homology, perspective), i.e. when each ray of the pencil passes through the corresponding point and each point of the range lies on the corresponding ray of the pencil. But since the equality of the composite relations entering into the expression of the theorem does not depend on the relative position of the range and the pencil, then, having cancelled the corresponding elements in some way, we can place the ranges and the pencil in any position on the plane and the theorem will obviously still remain valid, i.e., the composite relation of the range will still be equal to the composite relation of the pencil. Ranges and pencils having the same composite relation, but not generally located in the corresponding position, are called similar (homographically projective). Ranges and pencil will remain similar, no matter how we place them on the plane.
Two ranges and on two secants and (Fig. 1) are obviously similar ranges, but here they are in perspective, because the lines connecting the corresponding points pass through one point ; if we shift them and place them somehow on the plane, then the perspective will be completely broken, but the similarity will be preserved, and the points will correspond to the same points
In the same way, two pencils, having as their centres the points and in Fig. 1, are similar to each other, but in addition they are now in a corresponding position, because their corresponding rays intersect at points of one straight line; by somehow moving these pencils in the plane, we will violate this feature of their relative position, but we will not violate their similarity and between the same corresponding rays the equality of complex relations will be preserved.
Thus, no matter how we arrange the ranges , and the pencils on the plane, they will always present us with four geometric images, which are all pairwise similar to each other.
Let me now point out some considerations and consequences which follow directly from the fundamental theorem and which serve as the main starting points in the investigations of higher geometry.
1) When the secant is parallel to one of the rays of the pencil, for example, the ray , then the complex relation, as is not difficult to notice, turns into a simple relation ; the fourth point of the range is removed to an infinitely large distance and corresponds to it in the pencil, the only and completely definite ray parallel to the base of the range. With the slightest deviation of this ray in either direction, the corresponding point appears at a very large distance in different sides of the base. This consideration leads to the recognition on each line of only one infinitely distant point, which, like all other points, has one completely defined corresponding ray. When a line revolves continuously about a point , then the point corresponding to it also passes continuously from one position to another; thus the infinitely distant point re-establishes continuity between the ends of the straight line directed in different directions and, as it were, connects them. On similar considerations the concept of a unique infinitely distant line on a plane is established; both of these concepts play a very important role in higher geometry, for they eliminate all exceptions to general principles, and restore complete unity of research methods and complete community of results.
2) Since a complex relation in special cases turns into a simple geometric relation, it is clear that the equality of complex relations of two similar ranges is a generalisation of geometric proportion. From this it is clear why many questions that are very difficult to solve in elementary geometry by repeated application of proportion are very simply, in a few words, resolved with the help of the theory of complex relations. It should be added that in most cases, in order to apply the proportion, it is necessary to artificially compose or find the necessary similar triangles for this, whereas the ranges and pencils are almost always seen directly on the drawing. The complex ratio serves in higher geometry, like the proportion, to express all the quantitative relationships of the figure being studied, and with its help the results and theorems are very easily translated into the language of algebraic analysis.
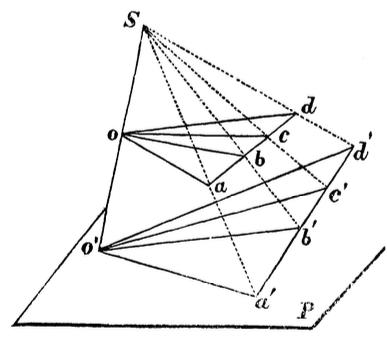
3) If we make a perspective projection of a range and a pencil from some point of view onto an arbitrary plane (Fig. 2), then we obtain in perspective a new range and pencil, which will obviously be similar to the first range and pencil, because the ranges and are obtained from the intersection of one and the same pencil . From this it is clear that the complex relationship does not change in perspective; and from this it follows that all the properties of a figure, depending only on the complex relationships that make up its pencils and ranges, necessarily belong to its perspective images. So we will find similar properties of a circle in its perspectives, that is, in its conical sections.
From the last drawing it is also evident how the concept of a complex relation can be extended to four planes passing through a common edge, and thus transfer the methods of higher geometry into three-dimensional space.
4) The study of the properties of plane figures by means of perspective presents the inconvenience that the figures must be examined in different planes. The theory of complex relationships completely eliminates this inconvenience, because the properties of figures, depending on the complex relationships of ranges and pencils, do not change at all with the change of their relative position; therefore, nothing prevents us from violating the original perspective position of the figures and combining them on one plane. From this follows the main idea of the theory of similar (homographic) and corresponding (homologous) figures. The theory of similarity, which finds its place in elementary geometry and is currently significantly expanded and enriched thanks to the ideas of higher geometry, also belongs to this theory as a special case.
5) From the theorem on the complex ratio there follows directly another and still more important principle of the transformation of figures: the principle of duality, or reciprocity. This principle in its simplest form is already contained in the theorem itself: the complex ratio of a range of points on one line is always equal to the complex ratio of a pencil of corresponding rays passing through one point. The theorem expresses, as we see, a property common to two corresponding, but essentially heterogeneous, images: a range and a pencil; in it one and the same thing is said, on the one hand, about points lying on one line, and on the other, about lines passing through one point. We saw above that the second part of the theorem is actually a consequence of the first and vice versa; From the fact that the complex relation of four points on a secant of a pencil is constant, it already followed that the complex relation of pencils based on the same four points is the same. We obtain the second part of the theorem from the first by a simple replacement of some elements by their corresponding ones, i.e., points by lines and vice versa. It is clear that the same will hold for all properties and theorems deduced with the help of the theory of complex relations. Every property proved with respect to points will necessarily have a corresponding property with respect to lines; for every theorem there will necessarily exist a reciprocal theorem, which says that there are 0 lines then there are 0 points, and vice versa. For every figure a reciprocal can be constructed, in which to every point of the curved line of the first figure there corresponds a tangent line and vice versa; and to every theorem on the points of the curve there necessarily corresponds a theorem on the tangents of the reciprocal curve. This is the beginning of the duality and reciprocity of geometric figures. This beginning, in spite of its simplicity and obviousness, is undoubtedly one of the most important acquisitions of the new geometry; thanks to it many investigations are greatly simplified and generalised. All problems, all constructions acquire the same dual character: the union of two points by a straight line is replaced in the mutual figure by the continuation of the lines to the point of intersection and vice versa; the intersection of a curve by a given straight line is the drawing of tangents from a given point, etc. This principle of duality was previously revealed mainly in the method of mutual polars, but not nearly as simply and obviously as it follows from the theory of complex relations.
6) The classical branch of geometry - the theory of conic sections - is developed with particular completeness and extraordinary elegance in advanced geometry. Here the doctrine of conic sections appears not as a problem to which the means of this science are successfully applied: it appears as a necessary development of the theory of complex relations. We have already said that the correspondence of elements of ranges, or pencils, does not depend on their special corresponding position, in which all the lines connecting the corresponding points of two ranges ( Fig. 1) pass through one point (), or all the corresponding rays of the pencils () intersect at points lying on the same line. When two similar pencils, or two ranges, are deduced from this special position, the question naturally arises, where will then lie the points of intersection of the corresponding rays of the pencils, or according to what law will be placed on the plane the straight lines connecting the corresponding points of the two ranges. The answer to this dual question lies in the dual mode of origin of conic sections. The most ingenious considerations convince us that in the first case the corresponding rays are always intersected on a perfectly definite conic section passing through the centres of both pencils; in the second case, the straight lines connecting the corresponding points of the range are always tangent to a certain conic section, or, as they say, encircle it; this conic section is tangent to the bases of both ranges. These two definitions of conic sections are reciprocal, so that by the law of duality we could directly deduce one of them from the other. The theory of conic sections is one of the most important and at the same time the most elegant branch of higher geometry; the innumerable variety of properties of these curves is deduced by means of the theory of complex ratio in an unusually simple way; very often, one drawing or very few words are enough to prove the point.
I should have mentioned here the theories of involution and transversals, the properties of four lines not passing through one point, and of four points not lying on one line; but this would require some very detailed explanations; I will limit myself to what has been said, fearing that I have already abused your attention.
In pointing out this series of ideas, which directly follow from the concept of a complex relation, we, of course, are far from exhausting all the means and do not discern all the aspects of higher geometry; we could also point out the use of imaginary quantities, the extension of the concept of ranges and pencils to curvilinear pencils and ranges, and much more. Hardly any other science adheres so consistently and steadfastly to one initial principle as higher geometry, and, in spite of this, it amazes us with the abundance and variety of the objects it studies. Not to mention geometric questions, which are more or less touched upon by this science, we note that it provides means even for solving soft questions of pure analysis. In Chasles' Higher Geometry and in his other works we find elegant and curious applications of the theory of similar ranges and pencils to the solution of systems of linear equations, to the solution of equations of the 2nd, 3rd and 4th degree, to the expansion of rational fractions and to the transformation of elliptic functions. Of course, all these articles are not of great importance with respect to the novelty of the results, because they are all developed in greater detail in their place; but in these investigations one cannot fail to see the originality and power of the methods inherent in the higher branches of geometry, and the close connection of these methods with algebraic methods. And who knows what new investigations and discoveries can be expected in the future, when these two powerful methods, analysis and geometry, will unite their forces and hand in hand, strengthening each other, will go along the path of research?
I have said that in our time a remarkable revolution is taking place in the direction of the mathematical sciences; not only advanced geometry bears witness to this. Everywhere, more and more every day, and perhaps more than anywhere else in analysis itself, new tendencies are being discovered. We no longer encounter those endless, tiresome, purely mechanical calculations which, after long and arduous labour, lead to conclusions of comparatively little importance; there is no longer that obscurity which often accompanied both the work itself and its results. Everything strives for simplicity and clarity; science has developed new, more perfect tools for research, promising it rich successes in the future. At the same time, the exact sciences are being simplified and become more accessible; many sections of higher mathematics are being updated and some of them, which were previously difficult even for specialists, are now brought to an almost elementary simplicity; it is enough to point out many sections of geometry, the theory of elliptic functions, the theory of potential. It is the duty of all of us to contribute with all our might to this good direction. Russian universities have found it possible in recent times to almost double the volume of teaching of physical and mathematical sciences. Unfortunately, our secondary educational institutions are far behind the secondary schools of all other European countries in this respect. It is desirable that circumstances develop more favourably than they do now, and for changing our course of elementary mathematics in accordance with the needs and resources of modern science.
The Moscow Mathematical Society serves the same useful purpose of developing and spreading the mathematical sciences in Russia. The more its existence is consolidated, the more successful will be its work, the closer it will be to achieving its goal, and the more benefit it will bring.
I have no doubt, Mr G, that we all sympathise with the activities of our recently established Society: let us unanimously wish it success and prosperity for the benefit of science and national education.
Last Updated June 2025