elliptic function
An elliptic function is an analytic function from C to C which is doubly periodic. That is, for two independent values of the complex number w, the functions f(z) and f(w+z) are the same.
It can also be regarded as the inverse function to certain integrals (called elliptic integrals) of the form 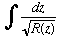 where R is a polynomial of degree 3 or 4.
where R is a polynomial of degree 3 or 4.
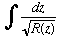 where is a polynomial of degree 3 or 4.
where is a polynomial of degree 3 or 4.
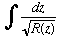 where is a polynomial of degree 3 or 4.
where is a polynomial of degree 3 or 4.