An overview of Babylonian mathematics
The Babylonians lived in Mesopotamia, a fertile plain between the Tigris and Euphrates rivers.
The region had been the centre of the Sumerian civilisation which flourished before 3500 BC. This was an advanced civilisation building cities and supporting the people with irrigation systems, a legal system, administration, and even a postal service. Writing developed and counting was based on a sexagesimal system, that is to say base 60. Around 2300 BC the Akkadians invaded the area and for some time the more backward culture of the Akkadians mixed with the more advanced culture of the Sumerians. The Akkadians invented the abacus as a tool for counting and they developed somewhat clumsy methods of arithmetic with addition, subtraction, multiplication and division all playing a part. The Sumerians, however, revolted against Akkadian rule and by 2100 BC they were back in control.
However the Babylonian civilisation, whose mathematics is the subject of this article, replaced that of the Sumerians from around 2000 BC The Babylonians were a Semitic people who invaded Mesopotamia defeating the Sumerians and by about 1900 BC establishing their capital at Babylon.
The Sumerians had developed an abstract form of writing based on cuneiform (i.e. wedge-shaped) symbols. Their symbols were written on wet clay tablets which were baked in the hot sun and many thousands of these tablets have survived to this day. It was the use of a stylus on a clay medium that led to the use of cuneiform symbols since curved lines could not be drawn. The later Babylonians adopted the same style of cuneiform writing on clay tablets.

Many of the tablets concern topics which, although not containing deep mathematics, nevertheless are fascinating. For example we mentioned above the irrigation systems of the early civilisations in Mesopotamia. These are discussed in [40] where Muroi writes:-
For more details of the Babylonian numerals, and also a discussion as to the theories why they used base 60, see our article on Babylonian numerals at THIS LINK.
The Babylonians divided the day into 24 hours, each hour into 60 minutes, each minute into 60 seconds. This form of counting has survived for 4000 years. To write 5h 25' 30", i.e. 5 hours, 25 minutes, 30 seconds, is just to write the sexagesimal fraction, . We adopt the notation 5; 25, 30 for this sexagesimal number.
As a base 10 fraction the sexagesimal number 5; 25, 30 is which is written as 5.425 in decimal notation.
For more details regarding this notation see our article on Babylonian numerals at THIS LINK.
Perhaps the most amazing aspect of the Babylonian's calculating skills was their construction of tables to aid calculation. Two tablets found at Senkerah on the Euphrates in 1854 date from 2000 BC. They give squares of the numbers up to 59 and cubes of the numbers up to 32. The table gives which stands for
The Babylonians used the formula
Division is a harder process. The Babylonians did not have an algorithm for long division. Instead they based their method on the fact that
We noted above that the Babylonians were famed as constructors of tables. Now these could be used to solve equations. For example they constructed tables for then, with the aid of these tables, certain cubic equations could be solved. For example, consider the equation
Again a table would have been looked up to solve the linear equation . They would consult the table to find and then multiply the sexagesimal number given in the table by . An example of a problem of this type is the following.
Suppose, writes a scribe, of of a certain quantity of barley is taken, 100 units of barley are added and the original quantity recovered. The problem posed by the scribe is to find the quantity of barley. The solution given by the scribe is to compute 0; 40 times 0; 40 to get 0; 26, 40. Subtract this from 1; 00 to get 0; 33, 20. Look up the reciprocal of 0; 33, 20 in a table to get 1;48. Multiply 1;48 by 1,40 to get the answer 3,0.
It is not that easy to understand these calculations by the scribe unless we translate them into modern algebraic notation. We have to solve
To solve a quadratic equation the Babylonians essentially used the standard formula. They considered two types of quadratic equation, namely
A problem on a tablet from Old Babylonian times states that the area of a rectangle is 1, 0 and its length exceeds its breadth by 7. The equation
In [10] Berriman gives 13 typical examples of problems leading to quadratic equations taken from Old Babylonian tablets.
If problems involving the area of rectangles lead to quadratic equations, then problems involving the volume of rectangular excavation (a "cellar") lead to cubic equations. The clay tablet BM 85200+ containing 36 problems of this type, is the earliest known attempt to set up and solve cubic equations. Hoyrup discusses this fascinating tablet in [26]. Of course the Babylonians did not reach a general formula for solving cubics. This would not be found for well over three thousand years.

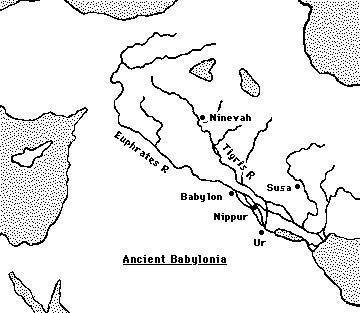
Here is a map of the region where the civilisation flourished.
The region had been the centre of the Sumerian civilisation which flourished before 3500 BC. This was an advanced civilisation building cities and supporting the people with irrigation systems, a legal system, administration, and even a postal service. Writing developed and counting was based on a sexagesimal system, that is to say base 60. Around 2300 BC the Akkadians invaded the area and for some time the more backward culture of the Akkadians mixed with the more advanced culture of the Sumerians. The Akkadians invented the abacus as a tool for counting and they developed somewhat clumsy methods of arithmetic with addition, subtraction, multiplication and division all playing a part. The Sumerians, however, revolted against Akkadian rule and by 2100 BC they were back in control.
However the Babylonian civilisation, whose mathematics is the subject of this article, replaced that of the Sumerians from around 2000 BC The Babylonians were a Semitic people who invaded Mesopotamia defeating the Sumerians and by about 1900 BC establishing their capital at Babylon.
The Sumerians had developed an abstract form of writing based on cuneiform (i.e. wedge-shaped) symbols. Their symbols were written on wet clay tablets which were baked in the hot sun and many thousands of these tablets have survived to this day. It was the use of a stylus on a clay medium that led to the use of cuneiform symbols since curved lines could not be drawn. The later Babylonians adopted the same style of cuneiform writing on clay tablets.

Here is one of their tablets
Many of the tablets concern topics which, although not containing deep mathematics, nevertheless are fascinating. For example we mentioned above the irrigation systems of the early civilisations in Mesopotamia. These are discussed in [40] where Muroi writes:-
It was an important task for the rulers of Mesopotamia to dig canals and to maintain them, because canals were not only necessary for irrigation but also useful for the transport of goods and armies. The rulers or high government officials must have ordered Babylonian mathematicians to calculate the number of workers and days necessary for the building of a canal, and to calculate the total expenses of wages of the workers.The Babylonians had an advanced number system, in some ways more advanced than our present systems. It was a positional system with a base of 60 rather than the system with base 10 in widespread use today.
There are several Old Babylonian mathematical texts in which various quantities concerning the digging of a canal are asked for. They are YBC 4666, 7164, and VAT 7528, all of which are written in Sumerian ..., and YBC 9874 and BM 85196, No. 15, which are written in Akkadian ... . From the mathematical point of view these problems are comparatively simple ...
For more details of the Babylonian numerals, and also a discussion as to the theories why they used base 60, see our article on Babylonian numerals at THIS LINK.
The Babylonians divided the day into 24 hours, each hour into 60 minutes, each minute into 60 seconds. This form of counting has survived for 4000 years. To write 5h 25' 30", i.e. 5 hours, 25 minutes, 30 seconds, is just to write the sexagesimal fraction, . We adopt the notation 5; 25, 30 for this sexagesimal number.
As a base 10 fraction the sexagesimal number 5; 25, 30 is which is written as 5.425 in decimal notation.
For more details regarding this notation see our article on Babylonian numerals at THIS LINK.
Perhaps the most amazing aspect of the Babylonian's calculating skills was their construction of tables to aid calculation. Two tablets found at Senkerah on the Euphrates in 1854 date from 2000 BC. They give squares of the numbers up to 59 and cubes of the numbers up to 32. The table gives which stands for
and so on up to .
The Babylonians used the formula
to make multiplication easier. Even better is their formula
which shows that a table of squares is all that is necessary to multiply numbers, simply taking the difference of the two squares that were looked up in the table then taking a quarter of the answer.
Division is a harder process. The Babylonians did not have an algorithm for long division. Instead they based their method on the fact that
so all that was necessary was a table of reciprocals. We still have their reciprocal tables going up to the reciprocals of numbers up to several billion. Of course these tables are written in their numerals, but using the sexagesimal notation we introduced above, the beginning of one of their tables would look like:
2 0; 30
3 0; 20
4 0; 15
5 0; 12
6 0; 10
8 0; 7, 30
9 0; 6, 40
10 0; 6
12 0; 5
15 0; 4
16 0; 3, 45
18 0; 3, 20
20 0; 3
24 0; 2, 30
25 0; 2, 24
27 0; 2, 13, 20
Now the table had gaps in it since , etc. are not finite base 60 fractions. This did not mean that the Babylonians could not compute , say. They would write
= (approx)
and these values, for example , were given in their tables. In fact there are fascinating glimpses of the Babylonians coming to terms with the fact that division by 7 would lead to an infinite sexagesimal fraction. A scribe would give a number close to and then write statements such as (see for example [5]):-
... an approximation is given since 7 does not divide.Babylonian mathematics went far beyond arithmetical calculations. In our article on Pythagoras's theorem in Babylonian mathematics at Pythagoras's theorem in Babylonian mathematics we examine some of their geometrical ideas and also some basic ideas in number theory. In this article we now examine some algebra which the Babylonians developed, particularly problems which led to equations and their solution.
We noted above that the Babylonians were famed as constructors of tables. Now these could be used to solve equations. For example they constructed tables for then, with the aid of these tables, certain cubic equations could be solved. For example, consider the equation
.
Let us stress at once that we are using modern notation and nothing like a symbolic representation existed in Babylonian times. Nevertheless the Babylonians could handle numerical examples of such equations by using rules which indicate that they did have the concept of a typical problem of a given type and a typical method to solve it. For example in the above case they would (in our notation) multiply the equation by and divide it by to get
= .
Putting this gives the equation
=
which could now be solved by looking up the table for the value of satisfying = . When a solution was found for then was found by . We stress again that all this was done without algebraic notation and showed a remarkable depth of understanding.
Again a table would have been looked up to solve the linear equation . They would consult the table to find and then multiply the sexagesimal number given in the table by . An example of a problem of this type is the following.
Suppose, writes a scribe, of of a certain quantity of barley is taken, 100 units of barley are added and the original quantity recovered. The problem posed by the scribe is to find the quantity of barley. The solution given by the scribe is to compute 0; 40 times 0; 40 to get 0; 26, 40. Subtract this from 1; 00 to get 0; 33, 20. Look up the reciprocal of 0; 33, 20 in a table to get 1;48. Multiply 1;48 by 1,40 to get the answer 3,0.
It is not that easy to understand these calculations by the scribe unless we translate them into modern algebraic notation. We have to solve
which is, as the scribe knew, equivalent to solving . This is why the scribe computed subtracted the answer from 1 to get , then looked up and so was found from multiplied by 100 giving 180 (which is 1; 48 times 1, 40 to get 3, 0 in sexagesimal).
To solve a quadratic equation the Babylonians essentially used the standard formula. They considered two types of quadratic equation, namely
and
where here were positive but not necessarily integers. The form that their solutions took was, respectively
and .
Notice that in each case this is the positive root from the two roots of the quadratic and the one which will make sense in solving "real" problems. For example problems which led the Babylonians to equations of this type often concerned the area of a rectangle. For example if the area is given and the amount by which the length exceeds the breadth is given, then the breadth satisfies a quadratic equation and then they would apply the first version of the formula above.
A problem on a tablet from Old Babylonian times states that the area of a rectangle is 1, 0 and its length exceeds its breadth by 7. The equation
is, of course, not given by the scribe who finds the answer as follows. Compute half of 7, namely 3; 30, square it to get 12; 15. To this the scribe adds 1, 0 to get 1; 12, 15. Take its square root (from a table of squares) to get 8; 30. From this subtract 3; 30 to give the answer 5 for the breadth of the triangle. Notice that the scribe has effectively solved an equation of the type by using .
In [10] Berriman gives 13 typical examples of problems leading to quadratic equations taken from Old Babylonian tablets.
If problems involving the area of rectangles lead to quadratic equations, then problems involving the volume of rectangular excavation (a "cellar") lead to cubic equations. The clay tablet BM 85200+ containing 36 problems of this type, is the earliest known attempt to set up and solve cubic equations. Hoyrup discusses this fascinating tablet in [26]. Of course the Babylonians did not reach a general formula for solving cubics. This would not be found for well over three thousand years.
References (show)
- A Aaboe, Episodes from the Early History of Mathematics (1964).
- R Calinger, A conceptual history of mathematics (Upper Straddle River, N. J., 1999).
- J Friberg, The third millenium roots of Babylonian mathematics. I. A method for the decipherment, through mathematical and metrological analysis, of proto-Sumerian and proto-Elamite semipictographic inscriptions, Department of Mathematics, University of Göteborg No. 9 (Göteborg, 1978).
- G Ifrah, A universal history of numbers : From prehistory to the invention of the computer (London, 1998).
- G G Joseph, The crest of the peacock (London, 1991).
- O Neugebauer and A Sachs, Mathematical Cuneiform Texts (New Haven, CT., 1945).
- B L van der Waerden, Science Awakening (Groningen, 1954).
- B L van der Waerden, Geometry and Algebra in Ancient Civilizations (New York, 1983).
- S K Adhikari, Babylonian mathematics, Indian J. Hist. Sci. 33 (1) (1998), 1-23.
- A E Berriman, The Babylonian quadratic equation, Math. Gaz. 40 (1956), 185-192.
- J K Bidwell, A Babylonian geometrical algebra, College Math. J. 17 (1) (1986), 22-31.
- L Brack-Bernsen and O Schmidt, Bisectable trapezia in Babylonian mathematics, Centaurus 33 (1) (1990), 1-38.
- E M Bruins, A contribution to the interpretation of Babylonian mathematics; triangles with regular sides, Nederl. Akad. Wetensch. Proc. Ser. A. Indagationes Math. 15 (1953), 412-422.
- E M Bruins, Fermat problems in Babylonian mathematics, Janus 53 (1966), 194-211.
- E M Bruins, On Babylonian geometry, Nederl. Akad. Wetensch. Proc. Ser. A. Indag. Math. 17 (1955), 16-23.
- E M Bruins, Refinement of approximations in Babylonian mathematics (Russian), Istor.-Mat. Issled. Vyp. 21 (1976), 61-70; 353.
- E M Bruins, Computation in the old Babylonian period, Janus 58 (1971), 222-267.
- M Caveing, La tablette babylonienne AO 17264 du Musée du Louvre et le problème des six frères, Historia Math. 12 (1) (1985), 6-24.
- S Démare-Lafont, Les partages successoraux paléobabyloniens, Histoire de fractions, fractions d'histoire, Sci. Networks Hist. Stud. 10 (Basel, 1992), 103-114; 404; 410.
- J Friberg, Methods and traditions of Babylonian mathematics. II. An old Babylonian catalogue text with equations for squares and circles, J. Cuneiform Stud. 33 (1) (1981), 57-64.
- S Gandz, A few notes on Egyptian and Babylonian mathematics, in Studies and Essays in the History of Science and Learning Offered in Homage to George Sarton on the Occasion of his Sixtieth Birthday, 31 August 1944 (New York, 1947), 449-462.
- S Gandz, Studies in Babylonian mathematics. I. Indeterminate analysis in Babylonian mathematics, Osiris 8 (1948), 12-40.
- S Gandz, Studies in Babylonian mathematics. II. Conflicting interpretations of Babylonian mathematics, Isis 31 (1940), 405-425.
- S Gandz, Studies in Babylonian mathematics. III. Isoperimetric problems and the origin of the quadratic equations, Isis 32 (1940), 101-115.
- R J Gillings and C L Hamblin, Babylonian sexagesimal reciprocal tables, Austral. J. Sci. 27 (1964), 139-141.
- J Hoyrup, The Babylonian cellar text BM 85200+ VAT 6599. Retranslation and analysis, Amphora (Basel, 1992), 315-358.
- J Hoyrup, Babylonian mathematics, in I Grattan-Guinness (ed.), Companion Encyclopedia of the History and Philosophy of the Mathematical Sciences (London, 1994), 21-29.
- S Ilic, M S Petkovic and D Herceg, A note on Babylonian square-root algorithm and related variants, Novi Sad J. Math. 26 (1) (1996), 155-162.
- D E Knuth, Ancient Babylonian algorithms, Twenty-fifth anniversary of the Association for Computing Machinery, Comm. ACM 15 (7) (1972), 671-677.
- D E Knuth, Errata: "Ancient Babylonian algorithms", Comm. ACM 19 (2) (1976), 108.
- H Lewy, Marginal notes on a recent volume of Babylonian mathematical texts, J. Amer. Oriental Soc. 67 (1947), 305-320.
- J S Liu, A general survey of Babylonian mathematics (Chinese), Sichuan Shifan Daxue Xuebao Ziran Kexue Ban 16 (1) (1993), 80-87.
- K Muroi, A circular field problem in the late Babylonian metrological-mathematical text W 23291-x, Ganita-Bharati 19 (1-4) (1997), 86-90.
- K Muroi, An enigmatic sentence in the old Babylonian table of exponents and logarithms, Historia Sci. (2) 6 (3) (1997), 229-230.
- K Muroi, Babylonian mathematics - ancient mathematics written in cuneiform writing (Japanese), in Studies on the history of mathematics (Kyoto, 1998), 160-171.
- K Muroi, Early Old Babylonian mathematical problems written in Sumerian, Historia Sci. (2) 7 (3) (1998), 199-203.
- K Muroi, Extraction of cube roots in Babylonian mathematics, Centaurus 31 (3-4) (1988), 181-188.
- K Muroi, Inheritance problems of Babylonian mathematics, Historia Sci. No. 34 (1988), 11-19.
- K Muroi, Interest calculation of Babylonian mathematics: new interpretations of VAT 8521 and VAT 8528, Historia Sci. No. 39 (1990), 29-34.
- K Muroi, Small canal problems of Babylonian mathematics, Historia Sci. (2) 1 (3) (1992), 173-180.
- K Muroi, The expressions of zero and of squaring in the Babylonian mathematical text VAT 7537, Historia Sci. (2) 1 (1) (1991), 59-62.
- K Muroi, Two harvest problems of Babylonian mathematics, Historia Sci. (2) 5 (3) (1996), 249-254.
- M A Powell Jr, The antecedents of old Babylonian place notation and the early history of Babylonian mathematics, Historia Math. 3 (1976), 417-439.
- A E Raik, From the early history of algebra. Quadratic equations among the Babylonians (Russian), Molotov. Gos. Univ. Uc. Zap. 8 (1) (1953), 31-63.
- A J Sachs, Babylonian mathematical texts. I. Reciprocals of regular sexagesimal numbers, J. Cuneiform Studies 1 (1947), 219-240.
- A J Sachs, Some metrological problems in Old-Babylonian mathematical texts, Bull. Amer. Schools of Oriental Research no. 96 (1944), 29-39.
- A J Sachs, Notes on fractional expressions in Old Babylonian mathematical texts, J. Near Eastern Studies 5 (1946), 203-214.
- G Sarton, Remarks on the study of Babylonian mathematics, Isis 31 (1940), 398-404.
- M Wygodski, Mathematics of the ancient Babylonians (Russian), Uspekhi Matem. Nauk 7 (1940), 102-153.
- M Wygodski, The mathematics of the ancient Babylonians (Russian), Uspekhi Matem. Nauk 8 (1941), 293-335.
Additional Resources (show)
Other websites about Babylonian mathematics:
Written by J J O'Connor and E F Robertson
Last Update December 2000
Last Update December 2000