Braid's Voluntary Exercises in Arithmetic

We know nothing about William Braid except for the above hand-written book of arithmetic exercises. It turned up at the bottom of a box of second-hand books that someone bought and they offered the book to Madras College.

The Head Master of Arithmetic and Book-Keeping at Madras College at the time was the Rev Daniel Fraser who lived at 8 North Bell Street, St Andrews. Around the middle of the book there is written in pencil: "24 March 1868. D Fraser." Fifty pages further on is written, again in pencil, "D Fraser. May 12th 1868."

In addition to the collection of arithmetic problems with solutions written by William Braid, he has written a Scots Proverb at the end of most of the problems. We begin by listing these Scots Proverbs in the order that they appear in the book. One or two are repeated and we list them twice as in Braid's book.

The Scots Proverbs

As the auld cock craws the young one learns.

A rowing stane gathers nae fog.

Mair by luck than good guiding.

I wad rather see't than hear tell o't.

Ill beef never made good broo.

Take your will o't as the cat did o' the haggis.

Rome was not bigged in ae day.

It is a sair field where a's slain.

A good word is as soon said as an ill.

A man of words, and not of deeds, is like a garden fou of weeds.

Better wait on the cook than the doctor.

He made a moon-light flitting.

A reeky house and a girning wife will make a man a fasheous life.

A nod of an honest man is enough.

Give a thing and tak a thing, that's the ill man's gowd ring.

Gie the de'il his due.

Every ane to his trade, quoth the browster to the bishop.

He's a good horse that never stumbles, and a better wife that never grumbles.

Experience teaches fools.

It is well that our faults are not written.

Delayes are dangerous.

He's like the sing'd cat, better than he's bonny.

A fool and his money are soon parted.

Better a finger aff than aye wagging.

Lang ere ye saddle a fool.

Keep the staff in your ain hand.

Good-ware make a quick market.

It is good sleeping in a hale shin.

It is good to be out of harms gate.

I wish you a muckle good o't as dogs get o'grass.

He's a proud fox that winna scrape his ain hole.

He that canna make sport shou'd mar nane.

She looks as if butter would not melt in her mou'.

Sair cravers are aye ill payers.

He sleeps as dogs when wives bake cakes.

He's a silly chief that can neither do nor say.

Laugh at leasure ye may greet ere night.

Keep something for a sair foot.

He that laughs at his ain sport spills the sport o't.

Learn you to an ill use and ye'll ca't custom.

Laith to bed and laith to rise.

Let na the plough stand to slay a mouse.

It keeps his nose at the grindstane.

Every thing hath an end and a pudding has twa.

Your purse was steeked when that was paid for.

Your tongue's nae slander.

Twa wits are better than ane.

A sillerless man gangs fast through the market.

Every man's tale is good till anither's be tauld.

Enough's as good as a feast.

Drink little that y may drink long.

Draff's good enough for swine.

Day-light will peep through a small hole.

I'll gie you a meeting as Mungo gae his mither.

A fool and his money are soon parted.

Any thing for a quiet life.

Better a toom house than an ill tenant.

Better a finger off than aye wagging.

Be a friend to yoursel and others will.

A toom purse makes a pratling merchant.

I wadna make flesh of ane an fish of another.

A wee mouse can creep under a great corn sack.

Auld sparrows are ill to tame.

Mettle is dangerous in a blind horse.

Time and thinking tame the strongest grief.

Want of wit is waur than want of health.

Well is that well does.

We canna baith sup and blaw.

We'll bark ourselves ere we buy dog.

Twa wits are better than ane.

Sair cravers are aye ill payers.

Say well and do well end with ae letter.

Silence grips the mouse.

Smooth waters run deep.

Speak good of pipers your father was a fiddler.

She looks as if butter would not melt in her mou'.

Better auld debts than auld sairs.

Better to be alane than in ill company.

The langer we live we see the mae fairlies.

The feathers bear away the flesh.

Dawted bairns do bear little.

All's well that ends well.

The Voluntary Exercises in Arithmetic are mostly elementary and the solutions for those near the beginning are not worth recording. However, we give an occasional example of a solution to illustrate William Braid's methods. Later on the examples become more interesting, really because they illustrate skills with which twenty-first century students would be less familiar. The examples dealing with repeating decimals fall into this category and we give more details of Braid's solutions (including his errors) when giving these. We have numbered the problems for convenience; they are not numbered in Braid's book.

Find the value of a ton of Gold, when 21805 Sovereigns weigh 384 lbs. avoirdupois.
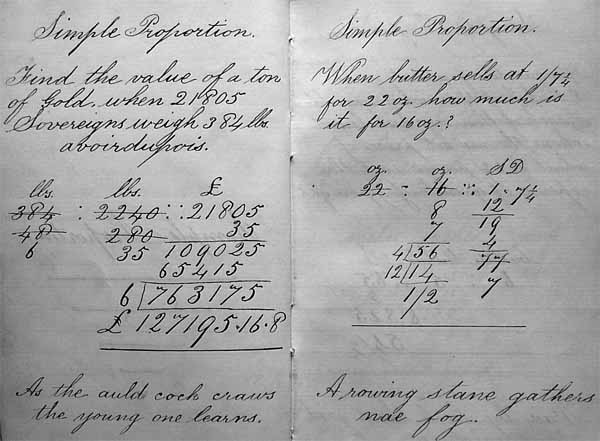
Solution. Braid writes
```
lbs   lbs        £
384 : 2240 :: 21805
 48    280
  6     35
```
He then multiplies
```
 21805
    35
------
109025
65415
------
763175
```
He then divides 763175 by 6 to obtain £ 127195 / 16 / 8. Notice that he can convert the decimal part of the answer into £sd in his head.
The price of gold is now (September 2010) about £ 750 per ounce (avoirdupois) and so since 1868 it seems that the price has increased by a factor of about 210.
When butter sells at 1 / $7\large\frac{1}{4}\normalsize$ (this is, one shilling, seven and a quarter pence) for 22 oz. how much is it for 16 oz.?

Solution. With similar working to the first example, Braid gets the correct answer 1 / 2 (this is, one shilling and two pence).
If a quarter of wheat yield 6 bushels flour what should a sack of flour of 5 bushels cost when the market price of wheat is 63 /- per qr. and the expense of grinding 2 /- per qr.?
If it require 33 yards of calico 25 inches wide to make curtains for a bed, how many yards of calico 30 inches wide will it require?
How much money at 3½ per cent will yield as much interest as £490 at 4 per cent?
A steeple projected a shadow to the distance of 33 yards when a 4 feet staff perpendicularly erected on level ground cast a shadow 5 feet 6 inches. What was the height of the steeple?
A bankrupt's debts amount to £ 5130 and his effects to £ 3729 / 18 / 9. How much can he offer his creditors per £?
Suppose the arms of a deceitful balance to be to each other as 12 to 11½. What weight will be required at the end of the shorter arm to counterbalance a weight of 46 lb. suspended from the end of the longer arm?
Find the value of a hhd. of sugar weighing net 12 cwt 3 qrs 21 lbs. at 9 / 9 per 14 lbs.

hhd stands for hogshead: a large barrel. The size of a hogshead is one of various measures for beer, wine, dry goods, ... .
Suppose the arms of a deceitful balance to be to each other as 10½ to 10 and suppose a weight of 35 lbs. hangs from the end of the shorter arm. What weight hung from the end of the longer arm will produce an equilibrium?
Find the value of a piece of sheet lead measuring $68\large\frac{1}{4}\normalsize$ square feet, 8 lbs. to a square foot at 42 / 6 per cwt.
Bought 2 cwt 3qrs 14 lb. of sugar for £ 13 / 2 / 7. At what must it retail at per lb. to clear 46 /- on the whole?
A piece of calico 25 inches wide is valued at 2 / 1 per yard. What should be the price per yard of another piece of the same quality 30 inches wide?
If the penny loaf weighs 9 oz 2 dr when wheat sells at 50 /- per quarter, what ought it to weigh when wheat sells at 70 /- per quarter?
Find the value of 1725 stones of hay at 64 /- per 100 stones.
Find the amount of 1386 gallons at £ 44 / 11 /- for 252 gallons.
A butcher buys a piece of linen measuring 26 yards at 2 / 7½ per yard. How much beef at 6 / 6 per stone must he give in return?
Find the insurance on £ 340 / 15 / 6 at 3 /- per cent.
If 3 cwt 13 lbs of soap cost £ 14 / 2 / 9 what will 7 cwt 2 qrs 25 lbs cost?

If I pay 11d for 66 oz. of bread when flour sells at 70 /- per sack, what ought I to pay for 20 oz. of bread when flour is at 63 /- per sack?
Solution. Braid writes
```
  oz     oz     d
  66 :   20 :: 11
  70 :   63
----   ----
4620 : 1260
```
He then multiplies 1260 by 11 to get 13860 and divides by 4620 to obtain 3d .
If 24 men cut down 128 acres in 36 days, in how many days will 12 men cut down 32 acres at that rate?
If 2 horses require 30 quarters of oats in 365 days, how many quarters at the same rate will 11 horses require in 73 days?
If 12 /- are given for the carriage of 2 cwt 3 qrs for 192 miles, how much should be given at that rate for the carriage of 8 cwt 1 qrs for 128 miles?
Find the interest of £ 456 / 12 /- for $4\large\frac{3}{4}\normalsize$ years at 4½ per cent.
Find the interest of £ 512 / 10 /- for 133 days at 5 per cent.
If the quartern loaf sells at 7½d when wheat sells at 50 /- a quarter, what ought the 6d loaf to weigh when wheat sells at 80 /- a quarter?
If 118 men eat 80 qrs of wheat in 108 days, how many qr will 88 men eat in a year and 107 days?
If 45 10d loaves can be made from 6 bushels of wheat, how many 8d loaves be got from 9 qrs?
If £ 100 gain £ 5 in a year, what will £ 650 gain in 219 days?
If 3 persons are boarded 4 weeks for £ 7, how long ought 14 persons to be boarded for £ 112?

Divide 739 acres 1 rood among A, B, C, and D according to their rents which are as follows. A's £ 200, B's £ 133 / 6 / 8, C's £113 / 7 / 9 and D's £78 / 11 / 2.

There are 4 roods in an acre, 10 (square) poles in a rood and $30\large\frac{1}{4}\normalsize$ square yards in a square pole.
Solution. Braid writes
```
  £ S d    £      Ac.Ro.


525/5/7 : 200 :: 739..1
```
He then converts the two sums of money to pence and the area to roods to obtain

126067 : 48000 :: 2957

He multiplies 48000 by 2957 and divides by 126067. After obtaining 1125 with remainder 110625, he multiples 110625 by 40 and continues to divide obtaining 35 with remainder 12655. He then gives the answer in acres, roods and (square) poles as 281..1.. $35\large\frac{12655}{126067}\normalsize$ . Although he doesn't say so, this is A's share.

He then carries out the same calculation for B's share obtaining Ac187..2.. $23\large\frac{50459}{126067}\normalsize$ .

He then carries out the same calculation for C's share obtaining Ac159..2.. $12\large\frac{10996}{126067}\normalsize$ .

He then carries out the same calculation for D's share but, despite carrying out the division never records the answer.
Divide a common consisting of 165 acres among A, B and C according to their rents which are £900, £1050 and £800 respectively.
A, B, C and D buy a ship. A pays for 6 shares, B for 7, C for 3 and D for 2. They receive of net freight for a voyage £ 315 / 14 / 6. How much of this sum ought each to receive?

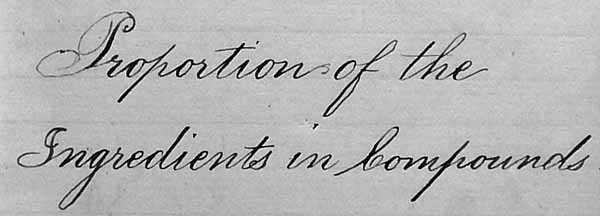
How many lbs. of raw sugar at 5d at 6d and at 7d per lb. must be mixed together to form a compound worth 6½d per lb?
Solution. Braid writes
```
5d   1 /2             1 @ 5d


6d   1 /2             1 @ 6d


7d   1+ 1 /2  + 1 /2    4 @ 7d 
```
He brackets the 3 lines on the left writing 6½d to the left of the bracket, and he brackets the 3 lines on the right writing Ans.
A bale of flannel containing 336 yards of which the average cost was 1 / 6 per yard consists of 4 kinds, which cost respectively 1 / 1, 1 / 3, 1 / 8 and 1 / 10 per yard. How many yards of each kind does it contain?

Solution. Braid obtains the ratios 4 : 2 : 3 : 5 with sum 14. He then computes 14 : 4 :: 336 to get 96 @ 1 / 1 . Also 14 : 2 :: 336 to get 48 @ 1 / 3 , 14 : 3 :: 336 to get 72 @ 1 / 8 , and 14 : 5 :: 336 to get 120 @ 1 / 10.
How many ounces of silver of 218 dwt. fine, of 220 dwt. fine and of 230 dwt. fine must be taken to form a mass of standard purity, that is 222 dwt. fine?

dwt stands for pennyweight: a unit of mass used for precious (and other) metals. A pennyweight is $\large\frac{1}{20}\normalsize$ of a Troy ounce and is 1.55 grams.

Solution. Braid obtains 4 @ 218, 1 @ 220, 1 @ 224, and 2 @ 230.

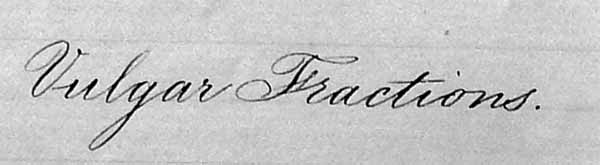
To find the greatest common measure of two numbers.
1080 and 1728.

Solution. Braid divides 1728 by 1080 to get 1 with remainder 448. He continues to divide 1080 by 648 which goes 1 with remainder 432. He then divides 1080 by 432 which gives 2 with remainder 216. Finally 1080 divided by 216 gives 5 with no remainder.

216 Ans.
To find the least common multiple of several numbers.
4, 9, 12 and 36.
4, 6, 8 and 12.

Solution. Braid solves both in the same way. For the first, he writes

4 . 9 . 12 . 36
He divides the even numbers by 2
2 . 9 . 6 . 18
He divides the even numbers by 2
1 . 9 . 3 . 9
He divides the multiples of 3 by 3
1 . 3 . 1 . 3
He divides the multiples of 3 by 3
1 . 1 . 1 . 1

2 × 2 × 3 × 3 = 36 Ans.
To reduce a mixed number to an improper fraction.
$15\large\frac{3}{4}\normalsize$ .
$8\large\frac{4}{5}\normalsize$ .
$12\large\frac{11}{12}\normalsize$ .
To reduce an improper fraction to a whole or mixed number.
$\large\frac{132}{12}\normalsize$ .
$\large\frac{357}{9}\normalsize$ .
$\large\frac{3415}{267}\normalsize$ .
To reduce a compound fraction to an equivalent simple fraction.
$\large\frac{3}{5}\normalsize$ of $\large\frac{4}{7}\normalsize$ of $\large\frac{3}{4}\normalsize$ .
$\large\frac{1}{2}\normalsize$ of $\large\frac{7}{10}\normalsize$ of $\large\frac{8}{13}\normalsize$ .
$\large\frac{5}{6}\normalsize$ of $\large\frac{4}{5}\normalsize$ of $\large\frac{9}{1}\normalsize$ .
$\large\frac{7}{9}\normalsize$ of $\large\frac{4}{5}\normalsize$ of $12\large\frac{1}{2}\normalsize$ .

Solution. For the first example Braid cancels the 4's and gives $\large\frac{9}{35}\normalsize$ Ans.

Similarly for the others always making all possible cancellations.
To reduce a vulgar fraction to its least terms.
$\large\frac{3456}{6048}\normalsize$ .
$\large\frac{1980}{3168}\normalsize$ .
$\large\frac{187500}{450000}\normalsize$ .
$\large\frac{3168}{4608}\normalsize$ .
$\large\frac{5{1\over2}}{22}\normalsize$ .

Solution. There is no indication of what cancellations Braid is making but he writes

$\large\frac{3456}{6048}\normalsize = \large\frac{384}{672}\normalsize = \large\frac{48}{84}\normalsize = \large\frac{8}{14}\normalsize = \large\frac{4}{7}\normalsize$ Ans.

$\large\frac{1980}{3168}\normalsize = \large\frac{220}{352}\normalsize = \large\frac{55}{88}\normalsize = \large\frac{5}{8}\normalsize$ Ans.

$\large\frac{187500}{450000}\normalsize = \large\frac{375}{900}\normalsize = \large\frac{75}{180}\normalsize = \large\frac{15}{36}\normalsize = \large\frac{5}{12}\normalsize$ Ans.

$\large\frac{3168}{4608}\normalsize = \large\frac{352}{512}\normalsize = \large\frac{44}{64}\normalsize = \large\frac{11}{16}\normalsize$ Ans.

$\large\frac{5{1\over2}}{22}\normalsize = \large\frac{11}{44}\normalsize = \large\frac{1}{4}\normalsize$ Ans.
To reduce fractions to a common denominator.
$\large\frac{2}{3}\normalsize , \large\frac{5}{8}\normalsize , \large\frac{7}{9}\normalsize$ .
$\large\frac{6}{7}\normalsize , \large\frac{2}{5}\normalsize , \large\frac{5}{12}\normalsize , \large\frac{3}{4}\normalsize$ .

Solution. Braid writes

$\large\frac{2}{3}\normalsize \times 8 \times 9 = \large\frac{144}{216}\normalsize$
$\large\frac{5}{8}\normalsize \times 3 \times 9 = \large\frac{135}{216}\normalsize$
$\large\frac{7}{9}\normalsize \times 3 \times 8 = \large\frac{168}{216}\normalsize$

[He might have been better to write

$\large\frac{2}{3}\normalsize \times \large\frac{8}{8}\normalsize \times \large\frac{9}{9}\normalsize = \large\frac{144}{216}\normalsize$ etc.]
To reduce fractions to their least common denominator.
$\large\frac{1}{2}\normalsize , \large\frac{7}{8}\normalsize , \large\frac{2}{3}\normalsize , \large\frac{11}{12}\normalsize$ .

Solution. Braid writes (again rather confusingly)

$\large\frac{1}{2}\normalsize \div 12 = \large\frac{12}{24}\normalsize$
$\large\frac{7}{8}\normalsize \div 3 = \large\frac{21}{24}\normalsize$
$\large\frac{2}{3}\normalsize \div 8 = \large\frac{16}{24}\normalsize$
$\large\frac{11}{12}\normalsize \div 2 = \large\frac{22}{24}\normalsize$ .
To reduce fractions to their least common denominator.
$\large\frac{1}{2}\normalsize$ , $\large\frac{2}{3}\normalsize$ , $\large\frac{5}{6}\normalsize$ , $\large\frac{7}{12}\normalsize$ .
To reduce a fraction from one denomination to another.
£ $\large\frac{(7\times 20\times 12\times 4)}{9}\normalsize$ .
Guin $\large\frac{(4\times 21\times 12)}{5}\normalsize$ .

A guinea is £ 1 / 1 /- or 21 shillings.
To reduce a fraction from one denomination to another.
far 5 / (6 × 4 × 12 × 20).
lbs (4 × 12 × 20) / 7.

A farthing is $\large\frac{1}{4}\normalsize$ pence.
To reduce a quantity to a fraction of any denomination.
(9 / 2d ) / (£ 1 / 1 /-).

Solution. Reducing to pence gives $\large\frac{110}{252}\normalsize$ = $\large\frac{55}{126}\normalsize$ Ans.
To reduce a quantity to a fraction of any denomination.
6 oz 2 dwt 10½ grains / 1 lb.

There are 20 pennyweights (dwt) in a (Troy) ounce and 24 grains in a pennyweight.
To find the value of a fraction.
£ $\large\frac{117}{95}\normalsize$ .
Addition in Vulgar fractions.
$\large\frac{3}{7}\normalsize , \large\frac{2}{9}\normalsize , \large\frac{1}{3}\normalsize , \large\frac{9}{10}\normalsize$ .
$\large\frac{3}{4}\normalsize , \large\frac{5}{6}\normalsize$ , and $\large\frac{8}{9}\normalsize$ .
$\large\frac{3}{4}\normalsize$ of $\large\frac{5}{6}\normalsize , 4\large\frac{}{5}\normalsize$ of $\large\frac{7}{8}\normalsize$ , and $\large\frac{4}{5}\normalsize$ .
$47\large\frac{3}{4}\normalsize , 29\large\frac{5}{7}\normalsize$ , and $35\large\frac{9}{14}\normalsize$ .
$98\large\frac{5}{8}\normalsize , 35\large\frac{11}{12}\normalsize$ , and $26\large\frac{5}{6}\normalsize$ .
$\large\frac{3}{8}\normalsize$ lb. troy, $\large\frac{5}{6}\normalsize$ lb., and $\large\frac{8}{9}\normalsize$ oz.
$\large\frac{11}{15}\normalsize$ guinea, $\large\frac{4}{5}\normalsize$ £, and $\large\frac{3}{5}\normalsize$ Shilling.

Solution. For the first example, Braid writes

$\large\frac{3}{7}\normalsize \times 90 = 270$
$\large\frac{2}{9}\normalsize \times 70 = 140$
$\large\frac{1}{3}\normalsize \times 210 = 210$
$\large\frac{9}{10}\normalsize \times 63 = 567$

He brackets all 4 lines on the right, writing 630 in the middle of the bracket.

Adding he gets 1187 which he divides by 630 to get $1\large\frac{557}{630}\normalsize$ .

There are 20 Troy ounces in a Troy pound.
Subtraction of Vulgar Fractions.
From 56 take $21 \large\frac{4}{15}\normalsize$ .
From 35 take $16 \large\frac{5}{16}\normalsize$ .
From $\large\frac{8}{9}\normalsize$ take $\large\frac{4}{13}\normalsize$ .
From $\large\frac{3}{8}\normalsize$ ton take $\large\frac{3}{5}\normalsize$ cwt.
From $\large\frac{6}{7}\normalsize$ £ take $\large\frac{3}{5}\normalsize$ guinea.
From £ $11\large\frac{4}{9}\normalsize$ take £ $3\large\frac{3}{8}\normalsize$ .
From $29\large\frac{5}{8}\normalsize$ take $16\large\frac{7}{8}\normalsize$ .
From $\large\frac{3}{4}\normalsize$ of $\large\frac{4}{5}\normalsize$ take $\large\frac{1}{9}\normalsize$ of $\large\frac{7}{10}\normalsize$ .
From $\large\frac{11}{12}\normalsize$ of $\large\frac{3}{8}\normalsize$ take $\large\frac{2}{3}\normalsize$ of $\large\frac{1}{7}\normalsize$ .

Solution. Here all fractions (and integers) are converted to a common denominator. For the first example, Braid writes

$\large\frac{56}{1}\normalsize \times 15 = 840$
$\large\frac{319}{15}\normalsize \times 1 = 319$

These two lines are bracketed on the right and 15 written behind the bracket. He subtracts 319 from 840 to get 521, then divides by 15 giving $34\large\frac{11}{15}\normalsize$ Ans.

Others fractions are solved in a similar way but the tons and cwt problem is solved by converting to

cwt. qrs. lbs. oz. drs.

and the money problem by converting to £sd (and fractions of a penny).
Multiplication of Vulgar Fractions.
Multiply $\large\frac{3}{5}\normalsize$ by $\large\frac{6}{7}\normalsize$ .
Multiply $\large\frac{5}{6}\normalsize$ by $\large\frac{7}{8}\normalsize$ .
Multiply $\large\frac{9}{10}\normalsize$ by $\large\frac{5}{6}\normalsize$ .
Multiply $\large\frac{3}{4}\normalsize$ by $\large\frac{4}{5}\normalsize$ by $\large\frac{5}{6}\normalsize$ .
Multiply $\large\frac{2}{7}\normalsize$ by $\large\frac{8}{9}\normalsize$ by $\large\frac{7}{8}\normalsize$ .
Multiply $\large\frac{3}{5}\normalsize$ of $\large\frac{7}{9}\normalsize$ by $\large\frac{4}{7}\normalsize$ of $\large\frac{2}{3}\normalsize$ .
Multiply $\large\frac{9}{16}\normalsize$ by $\large\frac{8}{1}\normalsize$ .
Multiply $\large\frac{11}{24}\normalsize$ by $\large\frac{12}{1}\normalsize$ .
Multiply $\large\frac{10}{13}\normalsize$ by $\large\frac{71}{1}\normalsize$ .
Multiply 617 by $5\large\frac{5}{6}\normalsize$ .
Multiply 894 by $21\large\frac{3}{4}\normalsize$ .
Multiply 536 by $67\large\frac{7}{8}\normalsize$ .
Multiply $14\large\frac{3}{7}\normalsize$ by $\large\frac{5}{8}\normalsize$ .
Multiply $29\large\frac{4}{9}\normalsize$ by $\large\frac{2}{3}\normalsize$ .
Multiply $85\large\frac{5}{6}\normalsize$ by $\large\frac{3}{4}\normalsize$ .
Multiply $92\large\frac{2}{5}\normalsize$ by $31\large\frac{4}{9}\normalsize$ .
Multiply $27\large\frac{11}{12}\normalsize$ by $8\large\frac{5}{6}\normalsize$ .

Solution. All are solved in the obvious way, doing all possible cancellations before multiplying.
Division of Vulgar Fractions.
Divide $\large\frac{8}{9}\normalsize$ by $\large\frac{2}{3}\normalsize$ .
Divide $\large\frac{7}{12}\normalsize$ by $\large\frac{5}{6}\normalsize$ .
Divide $\large\frac{3}{7}\normalsize$ by $\large\frac{6}{11}\normalsize$ .
Divide $\large\frac{21}{25}\normalsize$ by $\large\frac{14}{15}\normalsize$ .
Divide $\large\frac{8}{9}\normalsize$ by $\large\frac{2}{9}\normalsize$ .
Divide $\large\frac{8}{9}\normalsize$ by 4.
Divide $\large\frac{12}{13}\normalsize$ by 6.
Divide $\large\frac{11}{15}\normalsize$ by 8.
Divide 29 by $\large\frac{3}{4}\normalsize$ .
Divide 65 by $\large\frac{7}{9}\normalsize$ .
Divide 97 by $5\large\frac{4}{7}\normalsize$ .
Divide $\large\frac{3}{8}\normalsize$ by $5\large\frac{1}{2}\normalsize$ .
Divide $56\large\frac{5}{9}\normalsize$ by $\large\frac{3}{5}\normalsize$ .
Divide $69\large\frac{2}{11}\normalsize$ by $\large\frac{8}{9}\normalsize$ .
Divide $76\large\frac{1}{2}\normalsize$ by $36\large\frac{4}{7}\normalsize$ .

Solution. Braid does the obvious calculation of multiplying by the inverse. However, what he writes is rather confusing. For example, for the first example he makes the obvious cancellations but writes

$\large\frac{8}{9}\normalsize \div \large\frac{3}{2}\normalsize = \large\frac{4}{3}\normalsize$
$1\large\frac{1}{2}\normalsize$ Ans.

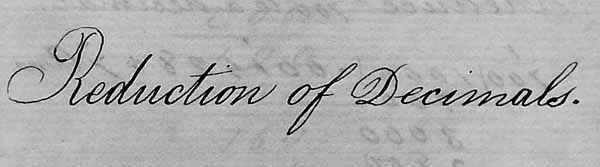
Reduce $\large\frac{3}{250}\normalsize$ to a decimal.

Solution. Long division gives .012 Ans.
Reduce $\large\frac{1}{700}\normalsize$ to a decimal.

Solution. Again long division until the remainder repeats when the answer is given correctly as a repeating decimal

.00142857

(Braid uses dots over the digits to indicate the beginning and end of a repeating group. We have used an "overline".)
Reduce $\large\frac{49}{52}\normalsize$ to a decimal.

Solution. Again long division until the remainder repeats when the answer is given correctly as a repeating decimal.

.94230769
Reduce $\large\frac{655}{2149}\normalsize$ to a decimal.

Solution. Long division gives .3047929+. It is not clear how he decides the number of places to calculate. In fact this fraction has a repeating part of length 306.
Reduce 157 yds 1 ft 3 in to a mile.

Solution. He divides 3 in by 12 to get .25 in, then 1.25 ft by 3 to get .416 yards, then 157.416 by 1760 to get .089441287 mile.
Reduce 1 rood 20 poles to an acre.
Reduce 5 hrs 48 min 50 sec of a day.
Reduce 17' 44'' 48''' to a degree.
Value .603125 acres.

Solution. He multiplies by 4 to get 2.412500 roods. Then he multiplies .412500 by 40 to get 16.500000 (square) poles, then .500000 by $30\large\frac{1}{4}\normalsize$ to get 15.125000. Finally he converts .125000 to $\large\frac{1}{8}\normalsize$ .
So the answer is 2 roods 16 (square) poles $15\large\frac{1}{8}\normalsize$ (square) yards.
Value .483125 miles.

Solution. He converts to furlongs, yds, ins.

(There are 8 furlongs in a mile, 220 yards in a furlong and 36 inches in a yard.)
Value 365.242264 days.

Solution. He converts to days, hours, minutes, seconds.
Value 57°.2957795.

Solution. He converts to degrees, minutes, seconds, thirds. [There are 60 thirds in a second.]
Value .416 ton.

Solution. He converts to cwt, qr, lbs, oz, dr.

(There are 4 quarters in a hundredweight, 28 pounds in a quarter, 16 ounces in a pound and 16 drams in an ounce.)
Value .83 mile.
Value .93 acre.
Value .242 day.
Reduce .4, .75, and .625 to vulgar fractions.

Solution. $\large\frac{4}{10}\normalsize = \large\frac{2}{5}\normalsize$ Ans.
$\large\frac{75}{100}\normalsize = \large\frac{15}{20}\normalsize = \large\frac{3}{4}\normalsize$ Ans.
$\large\frac{625}{1000}\normalsize = \large\frac{125}{200}\normalsize = \large\frac{25}{40}\normalsize = \large\frac{5}{8}\normalsize$ Ans.
Reduce .8125, .025, and .00875 to vulgar fractions.
Reduce $.64 \large\frac{3}{4}\normalsize , .006\large\frac{1}{8}\normalsize$ , and $.486\large\frac{7}{8}\normalsize$ to vulgar fractions.

Solution. $\large\frac{259}{400}\normalsize$ Ans.
$\large\frac{49}{8000}\normalsize$ Ans.
$\large\frac{3895}{8000}\normalsize = \large\frac{779}{1600}\normalsize$ Ans.
Reduce .3, .6, and .90 to vulgar fractions.

Solution. .3 = 3 /9 = 1 /3 Ans.
.6 = $\large\frac{6}{9}\normalsize = \large\frac{2}{3}\normalsize$ Ans.
.90 = $\large\frac{90}{99}\normalsize = \large\frac{10}{11}\normalsize$ Ans.
Reduce .63, .108, and .148 to vulgar fractions.

Solution. .63 = $\large\frac{63}{99}\normalsize = \large\frac{21}{33}\normalsize = \large\frac{7}{11}\normalsize$ Ans.
.108 = $\large\frac{108}{999}\normalsize = \large\frac{36}{333}\normalsize = \large\frac{12}{111}\normalsize = \large\frac{4}{37}\normalsize$ Ans.
.148 = $\large\frac{148}{999}\normalsize = \large\frac{4}{27}\normalsize$ Ans.
Reduce .14634, .857142, and .615384 to vulgar fractions.

Solution. .14634 = $\large\frac{14634}{99999}\normalsize = \large\frac{4878}{33333}\normalsize = \large\frac{1626}{11111}\normalsize = \large\frac{6}{41}\normalsize$ Ans.
.857742 = $\large\frac{857142}{999999}\normalsize = \large\frac{285714}{333333}\normalsize = \large\frac{95238}{111111}\normalsize = \large\frac{6}{7}\normalsize$ .
.615384 = $\large\frac{615384}{999999}\normalsize = \large\frac{205128}{333333}\normalsize = \large\frac{68376}{111111}\normalsize = \large\frac{22792}{37037}\normalsize = \large\frac{8}{13}\normalsize$ .
Reduce .416, .2083, and .06 to vulgar fractions.

He uses the following (cunning) device to deal with 0.ab .. cde .. f.
Subtract the (integer) ab .. c from ab .. cde .. f to get the numerator. The denominator is then length(de .. f) nines followed by length(ab .. c) zeros.

Solution. Subtracting 41 from 416 gives 375. Then
$\large\frac{375}{9000}\normalsize = \large\frac{5}{12}\normalsize$ Ans.

Subtracting 208 from 2083 gives 1875. Then
$\large\frac{1875}{9000}\normalsize = \large\frac{375}{1800}\normalsize = \large\frac{5}{24}\normalsize$ Ans.

$\large\frac{6}{90}\normalsize = \large\frac{2}{30}\normalsize = \large\frac{1}{15}\normalsize$ Ans.
Reduce .003, .0083, and .07954 to vulgar fractions.

Solution. .003 = $\large\frac{3}{900}\normalsize = \large\frac{1}{300}\normalsize$ Ans.

.0083 = $\large\frac{75}{9000}\normalsize = \large\frac{1}{120}\normalsize$ Ans. (Though he makes a copying error here!)

.07954 = $\large\frac{07947}{99900}\normalsize = \large\frac{7}{88}\normalsize$ Ans.
Reduce .0185, .0046296, and .7621951 to vulgar fractions.

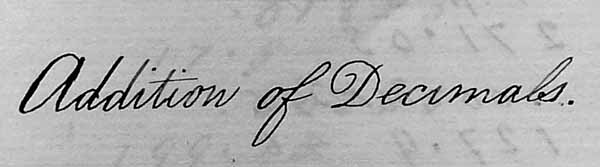
Add together 89.8125 + 271.05 + .375 + 127.9 + .01875 + 68.28945.

Solution. Add to get 557.4457 Ans.
Add together .01825 + 17.5 + .00375 + 199.25 + 144 + 310.0125.

Solution. Add to get 670.7845 Ans.
Reduce to decimals and then add together $21\large\frac{3}{4}\normalsize + 19\large\frac{7}{16}\normalsize + 4\large\frac{5}{8}\normalsize + 15\large\frac{1}{2}\normalsize + 83\large\frac{4}{5}\normalsize + 45\large\frac{3}{80}\normalsize$ .

Solution. Add 21.75, 19.4375, 4.625, 15.5, 83.8 and 45.0375 to get 190.15 Ans.
Reduce to decimals and then add together £ 21 / 10 /- + £ 8 / 17 / 6 + £ 4 / 18 / 9 + £ 3 / 3 / 6 + £ 9 / 18 / 7½ + £ 1 / 16 / 2¼.

Solution. Add 21.5, 8.875, 4.9375, 3.175, 9.93125, 1.809375 to get 50.2281125 Ans.
Add together .83 + 7.416 + .31855 + 6.25 + 4.38 + 29.627.
Solution. Braid expands the repeating decimals to sufficient places so that from that point on all are one digit repeats, then adds.
(He has to note that he gets a carry from the next column.)
```
   .83333|3
  7.41666|6
   .31855|0
  6.25000|0
  4.38888|8
 29.62777|7
-----------
 48.83521 6
```
Add together 17.5 +182.75 + .4 + 19.85 + .008125 + 89.655.

Solution. No repeating decimals so addition is routine.
Reduce and add together £ 44 / 7 / 6½ + £ 9 / 15 / 10 + £ 6 / 8 / 8 + £ 12 / 19 / 7 + £ 10 / 0 / 0¼ + £9 / 0 / 2½ + £ 13 / 9 / 5¾.
Solution. Reduce to decimals then add as in Problem 84. Braid writes
```
 44.3770833|3
  9.7916666|6
  6.4333333|3
 12.9791666|6
 10.1041666|6
  9.1041666|6
 13.4739625|0
-------------
106.06
```
There are a number of errors here but the answer is correct.
£ 10 / 0 / 0¼ = 10.0010416
£ 9 / 0 / 2½ = 9.010416
£ 13 / 9 / 5¾ = 13.4739583

Although one might believe that the first two errors are copying errors from Braid's rough work, the final error surely isn't a copying error. Either Braid worked out the correct answer adding £sd and then converted to decimals, or he copied the correct answer from somewhere else.
Reduce and add together $12\large\frac{1}{3}\normalsize + 3\large\frac{5}{6}\normalsize + 41\large\frac{5}{12}\normalsize + 85\large\frac{1}{8}\normalsize + 7\large\frac{1}{2}\normalsize +69\large\frac{2}{9}\normalsize + 5\large\frac{5}{24}\normalsize$ .
Solution. Reduce to decimals then add
```
 12.333|3
  3.833|3
 41.416|6
 85.125|0
  7.500|0
 69.222|2
  5.208|3
---------
224.638
```
Add together 9.45 + 5.3 + 13.83 + 1.76235 + 16.42135 + 157.025641 + 19.142857.
Solution. Braid expands the repeating decimals to sufficient places so that all have a repeating length of 6
```
  9.45454|545454
  5.33333|333333
 13.83333|333333
  1.76235|000000
 16.42135|135135
157.02564|102564
 19.14285|714285
----------------
222.97341 164106
```
Repeats of 1, 2, 3 and 6 all work with a repeat of 6. Notice how he has manipulated the repeat in the last two terms.
Reduce and add together $94\large\frac{3}{16}\normalsize + 58\large\frac{5}{27}\normalsize + 152\large\frac{12}{13}\normalsize + 14\large\frac{2}{3}\normalsize + 45\large\frac{6}{7}\normalsize + 9\large\frac{7}{24}\normalsize + 76\large\frac{9}{11}\normalsize$ .
Solution. Braid expands the repeating decimals to sufficient places. Notice that again a repeat length of 6 suffices for all.
```
 94.1875|000000
 58.1851|851851
152.9230|769230
 14.6666|666666
 45.8571|428571
  9.2916|666666
 76.8181|818181
---------------
541.9294 201169
```
Add together .83 + 7.416 + .31855 + 6.25 + 4.38 + 29.627.

From 5.53125 take 1.25.
From 213.5 take 1.8125.
From .45 take .0045.
From 31 take .875.
Reduce to decimals and from $173\large\frac{1}{5}\normalsize$ take $99\large\frac{1}{16}\normalsize$ .
Reduce to decimals and from £ 81 / 12 / 6 take £ 37 / 9 / 1 $\large\frac{1}{2}\normalsize$ .

Solution. Converting to decimals gives
£ 81.625 - £ 37.45625 = £ 44.16875.
From 96.3135 take 37.3.
Solution.
```
 69.3135
 37.33333
 --------
 31.98016
```

From 81.7175 take 73.561.

Solution.

81.7175
73.5615615
------------
 8.1559384

From 34.815 take 5.47325.

Solution.

34.85185185
 5.47325
-------------
29.37860185

From 21.453 take 13.72.
Solution.
```
21.453453
13.727272
---------
 7.726180
```
Reduce to decimals and from 915 /36 take 475 /9 .
Solution.
```
91.138
47.555
-------
43.583
```
Reduce to decimals and from £9 1 / 18 / 8½ take £ 55 / 4 / 11¾.

Solution. Converting to decimals gives
£ 91.9354166 - £ 55.2489583 = £ 36.6864583.

Multiply 8.25 by 4.5.

Solution. Long multiplication

  8.25
 ×4.5
------
 4 125
33 00
------
37.125

Multiply .24165 by .175.

Solution. Long multiplication gives .04228875
Multiply .0825 by .0625.

Solution. Long multiplication gives .00515625
Multiply .00875 by 6.5.

Solution. Long multiplication gives .056875
Multiply .3518 by 124.

Solution. Long multiplication gives 43.6232
Multiply 5.425 by 2.125.

Solution. Long multiplication gives 11.528125
Multiply .1234 by .134.

Solution. Long multiplication gives .0165356
Multiply 47.55 by .243.

Solution. Long multiplication gives 11.55465
Multiply 63.416 by 32.5.
Solution. This is more interesting because of the 6 repeating. Long multiplication gives
```
  63.416
 ×32.5
---------
  31 7083
 126 8333
1902 4999
---------
2061.0416
```
Notice that Braid knows how to multiply repeating decimals by single digits.
Multiply 5.683 by 475.

Solution. Long multiplication gives 2699.583
Multiply .49838 by 12.64.

Solution. Long multiplication gives 6.299635
Multiply 365.481 by .00325.
Solution. Long multiplication gives (according to Braid)
```
 365.481
 ×  .00325
----------
   1827409
   7309636
1 09644545
----------
1.18781590
```
Braid has made an error in his repeats. In the second row 36 should repeat, not 636. In the answer 90 should repeat not 590. So the correct answer should be 1.18781590
Multiply .27185 by 1.426.
Solution. Long multiplication gives
```
   .27185
 ×1.426
 --------
   163111
   543703
 10874074
 27185185
---------
.38766074
```
This is the correct answer. Notice now that Braid can multiply length 3 repeats by a single digit.
Multiply 8.769230 by 786.4.
Solution. Long multiplication gives
```
    8.769230
  786.4
    ---------
    3 5076923
   52 6153846
  701 5384613
 6138 4615384
 ------------
 6896.1230769
```
This is the correct answer but there is a copying error in the last figure of the third line which should be 5 rather than 3.
Multiply .92937 by 1500.
Solution. Long multiplication gives
```
 .92937
 ×1500
 -------
 464689
 92937
---------
1394.069
```
This is the correct answer.
Multiply 92.25 by.3.
Solution. Long multiplication gives
```
  92.25
  × .3
---------
30.7518
```
I have no idea if Braid can multiply by .3. I can do the sum by dividing 92.25 by 3 but this doesn't appear to be what Braid does.

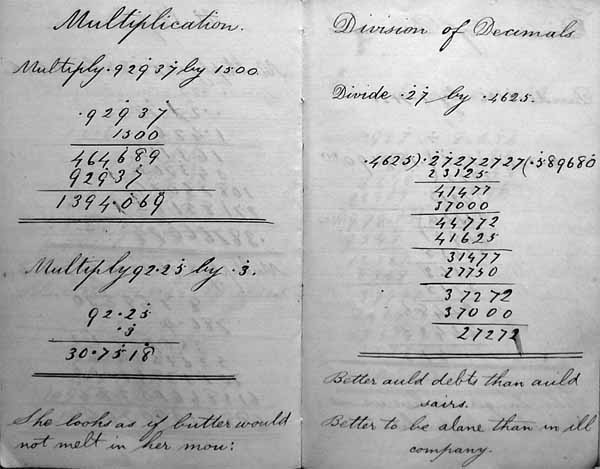
Divide .27 by .4625.

Solution. Long division gives .589680 after which the remainder is 27. Hence the answer is .589680
Divide .5136 by 2.715.

Solution. Braid divides using long division and gives up after .189190. In fact he would have to go a long way since this decimal has a repeating sequence 180 digits long.
Divide .987 by 8.634

Solution. Braid, after some calculation, ends up dividing 978 by 8548 and gets .1141 (actually he forgets to put the decimal point in). He should have divided 977.9 by 8548 and the correct answer is then .11440102948058025269...
Divide 358.3 by 472.55.

Solution. Braid gets .758297 and, finding no repeat, gives up (actually again he forgets to put the decimal point in).

Written by J J O'Connor and E F Robertson
Last Update September 2010