Chinese numerals
In 1899 a major discovery was made at the archaeological site at the village of Xiao dun in the An-yang district of Henan province. Thousands of bones and tortoise shells were discovered there which had been inscribed with ancient Chinese characters. The site had been the capital of the kings of the Late Shang dynasty (this Late Shang is also called the Yin) from the 14th century BC. The last twelve of the Shang kings ruled here until about 1045 BC and the bones and tortoise shells discovered there had been used as part of religious ceremonies. Questions were inscribed on one side of a tortoise shell, the other side of the shell was then subjected to the heat of a fire, and the cracks which appeared were interpreted as the answers to the questions coming from ancient ancestors.
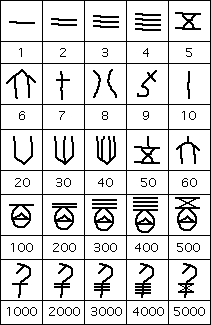
The importance of these finds, as far as learning about the ancient Chinese number system, was that many of the inscriptions contained numerical information about men lost in battle, prisoners taken in battle, the number of sacrifices made, the number of animals killed on hunts, the number of days or months, etc. The number system which was used to express this numerical information was based on the decimal system and was both additive and multiplicative in nature. Here is a selection of the symbols that were used.
By having multiplicative properties we mean that 200 is represented by the symbol for 2 and the symbol for 100, 300 is represented by the symbol for 3 and the symbol for 100, 400 is represented by the symbol for 4 and the symbol for 100, etc. Similarly 2000 is represented by the symbol for 2 and the symbol for 1000, 3000 is represented by the symbol for 3 and the symbol for 1000, 4000 is represented by the symbol for 4 and the symbol for 1000, etc. There was also a symbol for 10000 which we have not included in the illustration above but it took the form of a scorpion. However larger numbers have not been found, the largest number discovered on the Shang bones and tortoise shells being 30000.
The additive nature of the system was that symbols were juxtaposed to indicate addition, so that 4359 was represented by the symbol for 4000 followed by the symbol for 300, followed by the symbol of 50 followed by the symbol for 9. Here is the way 4359 would appear: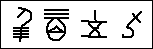
Now this system is not a positional system so it had no need for a zero. For example the number 5080 is represented by: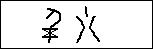
Because we have not illustrated many numbers above here is one further example of a Chinese oracular number. Here is 8873: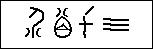
There are a number of fascinating questions which we can consider about this number system. Although the representation of the numbers 1, 2, 3, 4 needs little explanation, the question as to why particular symbols are used for the other digits is far less obvious. Two main theories have been put forward.
The first theory suggests that the symbols are phonetic. By this we mean that since the number nine looks like a fish hook, then perhaps the sound of the word for 'nine' in ancient Chinese was close to the sound of the word for 'fish hook'. Again the symbol for 1000 is a 'man' so perhaps the word for 'thousand' in ancient Chinese was close to the sound of the word for 'man'. To take an example from English, the number 10 is pronounced 'ten'. This sounds like 'hen' so a symbol for a hen might be appropriate, perhaps modified so that the reader knew that the symbol represented 'ten' rather than 'hen'.
A second theory about the symbols comes from the fact that numbers, and in fact all writing in this Late Shang period, were only used as part of religious ceremonies. We have explained above how the inscriptions were used by soothsayers, who were the priests of the time, in their ceremonies. This theory suggests that the number symbols are of religious significance. Of course it is possible that some of the symbols are explained by the first of these theories, while others are explained by the second. Again symbols such as the scorpion may simply have been used since swarms of scorpions meant "a large number' to people at that time. Perhaps the symbol for 100 represents a toe (it does look like one), and one might explain this if people at the time counted up to ten on their fingers, then 100 for each toe, and then 1000 for the 'man' having counted 'all' parts of the body.
The symbols we have illustrated evolved somewhat over time but were surprisingly stable in form. However a second form of Chinese numerals began to be used from the 4th century BC when counting boards came into use. A counting board consisted of a checker board with rows and columns. Numbers were represented by little rods made from bamboo or ivory. A number was formed in a row with the units placed in the right most column, the tens in the next column to the left, the hundreds in the next column to the left etc. The most significant property of representing numbers this way on the counting board was that it was a natural place valued system. One in the right most column represented 1, while one in the adjacent column to the left represented 10 etc.
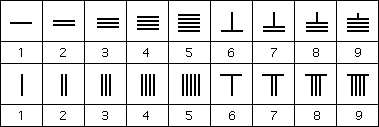
Now the numbers from 1 to 9 had to be formed from the rods and a fairly natural way was found.
Here are two possible representations:
The biggest problem with this notation was that it could lead to possible confusion. What was ||| ? It could be 3, or 21, or 12, or even 111. Rods moving slightly along the row, or not being placed centrally in the squares, would lead to the incorrect number being represented. The Chinese adopted a clever way to avoid this problem. They used both forms of the numbers given in the above illustration. In the units column they used the form in the lower row, while in the tens column they used the form in the upper row, continuing alternately. For example 1234 is represented on the counting board by: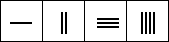 and 45698 by:
and 45698 by: 
There was still no need for a zero on the counting board for a square was simply left blank. The alternating forms of the numbers again helped to show that there was indeed a space. For example 60390 would be represented as:
Ancient arithmetic texts described how to perform arithmetic operations on the counting board. For example Sun Zi, in the first chapter of the Sunzi suanjing Ⓣ, gives instructions on using counting rods to multiply, divide, and compute square roots.
Xiahou Yang's Xiahou Yang suanjing Ⓣ written in the 5th century AD notes that to multiply a number by 10, 100, 1000, or 10000 all that needs to be done is that the rods on the counting board are moved to the left by 1, 2, 3, or 4 squares. Similarly to divide by 10, 100, 1000, or 10000 the rods are moved to the right by 1, 2, 3, or 4 squares. What is significant here is that Xiahou Yang seems to understand not only positive powers of 10 but also decimal fractions as negative powers of 10. This illustrates the significance of using counting board numerals.
Now the Chinese counting board numbers were not just used on a counting board, although this is clearly their origin. They were used in written texts, particularly mathematical texts, and the power of the place valued notation led to the Chinese making significant advances. In particular the "tian yuan" or "coefficient array method" or "method of the celestial unknown" developed out of the counting board representation of numbers. This was a notation for an equation and Li Zhi gives the earliest source of the method, although it must have been invented before his time.
In about the fourteenth century AD the abacus came into use in China. Certainly this, like the counting board, seems to have been a Chinese invention. In many ways it was similar to the counting board, except instead of using rods to represent numbers, they were represented by beads sliding on a wire. Arithmetical rules for the abacus were analogous to those of the counting board (even square roots and cube roots of numbers could be calculated) but it appears that the abacus was used almost exclusively by merchants who only used the operations of addition and subtraction.
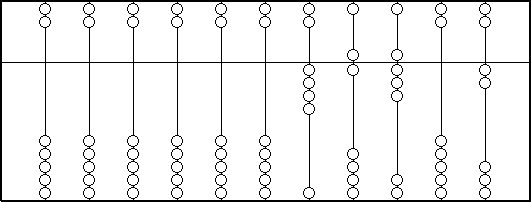
Here is an illustration of an abacus showing the number 46802.
For numbers up to 4 slide the required number of beads in the lower part up to the middle bar. For example on the right most wire two is represented. For five or above, slide one bead above the middle bar down (representing 5), and 1, 2, 3 or 4 beads up to the middle bar for the numbers 6, 7, 8, or 9 respectively. For example on the wire three from the right hand side the number 8 is represented (5 for the bead above, three beads below).
One might reasonably ask why each wire contains enough beads to represent 15. This was to make the intermediate working easier so that in fact numbers bigger than 9 could be stored on a single wire during a calculation, although by the end such "carries" would have to be taken over to the wire to the left.

The importance of these finds, as far as learning about the ancient Chinese number system, was that many of the inscriptions contained numerical information about men lost in battle, prisoners taken in battle, the number of sacrifices made, the number of animals killed on hunts, the number of days or months, etc. The number system which was used to express this numerical information was based on the decimal system and was both additive and multiplicative in nature. Here is a selection of the symbols that were used.
By having multiplicative properties we mean that 200 is represented by the symbol for 2 and the symbol for 100, 300 is represented by the symbol for 3 and the symbol for 100, 400 is represented by the symbol for 4 and the symbol for 100, etc. Similarly 2000 is represented by the symbol for 2 and the symbol for 1000, 3000 is represented by the symbol for 3 and the symbol for 1000, 4000 is represented by the symbol for 4 and the symbol for 1000, etc. There was also a symbol for 10000 which we have not included in the illustration above but it took the form of a scorpion. However larger numbers have not been found, the largest number discovered on the Shang bones and tortoise shells being 30000.
The additive nature of the system was that symbols were juxtaposed to indicate addition, so that 4359 was represented by the symbol for 4000 followed by the symbol for 300, followed by the symbol of 50 followed by the symbol for 9. Here is the way 4359 would appear:
Now this system is not a positional system so it had no need for a zero. For example the number 5080 is represented by:
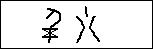
Because we have not illustrated many numbers above here is one further example of a Chinese oracular number. Here is 8873:
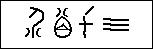
There are a number of fascinating questions which we can consider about this number system. Although the representation of the numbers 1, 2, 3, 4 needs little explanation, the question as to why particular symbols are used for the other digits is far less obvious. Two main theories have been put forward.
The first theory suggests that the symbols are phonetic. By this we mean that since the number nine looks like a fish hook, then perhaps the sound of the word for 'nine' in ancient Chinese was close to the sound of the word for 'fish hook'. Again the symbol for 1000 is a 'man' so perhaps the word for 'thousand' in ancient Chinese was close to the sound of the word for 'man'. To take an example from English, the number 10 is pronounced 'ten'. This sounds like 'hen' so a symbol for a hen might be appropriate, perhaps modified so that the reader knew that the symbol represented 'ten' rather than 'hen'.
A second theory about the symbols comes from the fact that numbers, and in fact all writing in this Late Shang period, were only used as part of religious ceremonies. We have explained above how the inscriptions were used by soothsayers, who were the priests of the time, in their ceremonies. This theory suggests that the number symbols are of religious significance. Of course it is possible that some of the symbols are explained by the first of these theories, while others are explained by the second. Again symbols such as the scorpion may simply have been used since swarms of scorpions meant "a large number' to people at that time. Perhaps the symbol for 100 represents a toe (it does look like one), and one might explain this if people at the time counted up to ten on their fingers, then 100 for each toe, and then 1000 for the 'man' having counted 'all' parts of the body.
The symbols we have illustrated evolved somewhat over time but were surprisingly stable in form. However a second form of Chinese numerals began to be used from the 4th century BC when counting boards came into use. A counting board consisted of a checker board with rows and columns. Numbers were represented by little rods made from bamboo or ivory. A number was formed in a row with the units placed in the right most column, the tens in the next column to the left, the hundreds in the next column to the left etc. The most significant property of representing numbers this way on the counting board was that it was a natural place valued system. One in the right most column represented 1, while one in the adjacent column to the left represented 10 etc.

Now the numbers from 1 to 9 had to be formed from the rods and a fairly natural way was found.
Here are two possible representations:
The biggest problem with this notation was that it could lead to possible confusion. What was ||| ? It could be 3, or 21, or 12, or even 111. Rods moving slightly along the row, or not being placed centrally in the squares, would lead to the incorrect number being represented. The Chinese adopted a clever way to avoid this problem. They used both forms of the numbers given in the above illustration. In the units column they used the form in the lower row, while in the tens column they used the form in the upper row, continuing alternately. For example 1234 is represented on the counting board by:
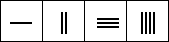 and 45698 by:
and 45698 by: 
There was still no need for a zero on the counting board for a square was simply left blank. The alternating forms of the numbers again helped to show that there was indeed a space. For example 60390 would be represented as:

Ancient arithmetic texts described how to perform arithmetic operations on the counting board. For example Sun Zi, in the first chapter of the Sunzi suanjing Ⓣ, gives instructions on using counting rods to multiply, divide, and compute square roots.
Xiahou Yang's Xiahou Yang suanjing Ⓣ written in the 5th century AD notes that to multiply a number by 10, 100, 1000, or 10000 all that needs to be done is that the rods on the counting board are moved to the left by 1, 2, 3, or 4 squares. Similarly to divide by 10, 100, 1000, or 10000 the rods are moved to the right by 1, 2, 3, or 4 squares. What is significant here is that Xiahou Yang seems to understand not only positive powers of 10 but also decimal fractions as negative powers of 10. This illustrates the significance of using counting board numerals.
Now the Chinese counting board numbers were not just used on a counting board, although this is clearly their origin. They were used in written texts, particularly mathematical texts, and the power of the place valued notation led to the Chinese making significant advances. In particular the "tian yuan" or "coefficient array method" or "method of the celestial unknown" developed out of the counting board representation of numbers. This was a notation for an equation and Li Zhi gives the earliest source of the method, although it must have been invented before his time.
In about the fourteenth century AD the abacus came into use in China. Certainly this, like the counting board, seems to have been a Chinese invention. In many ways it was similar to the counting board, except instead of using rods to represent numbers, they were represented by beads sliding on a wire. Arithmetical rules for the abacus were analogous to those of the counting board (even square roots and cube roots of numbers could be calculated) but it appears that the abacus was used almost exclusively by merchants who only used the operations of addition and subtraction.

Here is an illustration of an abacus showing the number 46802.
For numbers up to 4 slide the required number of beads in the lower part up to the middle bar. For example on the right most wire two is represented. For five or above, slide one bead above the middle bar down (representing 5), and 1, 2, 3 or 4 beads up to the middle bar for the numbers 6, 7, 8, or 9 respectively. For example on the wire three from the right hand side the number 8 is represented (5 for the bead above, three beads below).
One might reasonably ask why each wire contains enough beads to represent 15. This was to make the intermediate working easier so that in fact numbers bigger than 9 could be stored on a single wire during a calculation, although by the end such "carries" would have to be taken over to the wire to the left.
References (show)
- G Ifrah, The universal history of numbers (London, 1998).
- J-C Martzloff, A history of Chinese mathematics (Berlin-Heidelberg, 1997).
- J-C Martzloff, Histoire des mathématiques chinoises (Paris, 1987).
- F C Scesney, The Chinese abacus (New York, 1944).
- D C Cheng, The use of computing rods in China, Archiv der Mathematik und Physic 32 (1925), 492-499.
- J Needham, Mathematics and the science of the heavens and the earth, in J Needham, Science and civilisation in China (Cambridge, 1959).
Additional Resources (show)
Other websites about Chinese numerals:
Written by J J O'Connor and E F Robertson
Last Update January 2004
Last Update January 2004