The Indian Sulbasutras
The Vedic people probably entered India about 1500 BC from the region that today is Iran. The word Vedic describes the religion of these people and the name comes from their collections of sacred texts known as the Vedas. The texts date from about the 15th to the 5th century BC and were used for sacrificial rites which were the main feature of the religion. There was a ritual which took place at an altar where food, also sometimes animals, were sacrificed. The Vedas contain recitations and chants to be used at these ceremonies. Later prose was added called Brahmanas which explained how the texts were to be used in the ceremonies. They also tell of the origin and the importance of the sacrificial rites themselves.
The Sulbasutras are appendices to the Vedas which give rules for constructing altars. If the ritual sacrifice was to be successful then the altar had to conform to very precise measurements. The people made sacrifices to their gods so that the gods might be pleased and give the people plenty food, good fortune, good health, long life, and lots of other material benefits. For the gods to be pleased everything had to be carried out with a very precise formula, so mathematical accuracy was seen to be of the utmost importance. We should also note that there were two types of sacrificial rites, one being a large public gathering while the other was a small family affair. Different types of altars were necessary for the two different types of ceremony.
All that is known of Vedic mathematics is contained in the Sulbasutras. This in itself gives us a problem, for we do not know if these people undertook mathematical investigations for their own sake, as for example the ancient Greeks did, or whether they only studied mathematics to solve problems necessary for their religious rites. Some historians have argued that mathematics, in particular geometry, must have also existed to support astronomical work being undertaken around the same period.
Certainly the Sulbasutras do not contain any proofs of the rules which they describe. Some of the rules, such as the method of constructing a square of area equal to a given rectangle, are exact. Others, such as constructing a square of area equal to that of a given circle, are approximations. We shall look at both of these examples below but the point we wish to make here is that the Sulbasutras make no distinction between the two. Did the writers of the Sulbasutras know which methods were exact and which were approximations?
The Sulbasutras were written by a scribe, although he was not the type of scribe who merely makes a copy of an existing document but one who put in considerable content and all the mathematical results may have been due to these scribes. We know nothing of the men who wrote the Sulbasutras other than their names and a rough indication of the period in which they lived. Like many ancient mathematicians our only knowledge of them is their writings. The most important of these documents are the Baudhayana Sulbasutra written about 800 BC and the Apastamba Sulbasutra written about 600 BC. Historians of mathematics have also studied and written about other Sulbasutras of lesser importance such as the Manava Sulbasutra written about 750 BC and the Katyayana Sulbasutra written about 200 BC.
Let us now examine some of the mathematics contained within the Sulbasutras. The first result which was clearly known to the authors is Pythagoras's theorem. The Baudhayana Sulbasutra gives only a special case of the theorem explicitly:-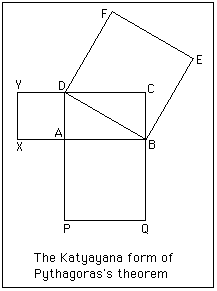
The diagram on the right illustrates this result.
Note here that the results are stated in terms of "ropes". In fact, although sulbasutras originally meant rules governing religious rites, sutras came to mean a rope for measuring an altar. While thinking of explicit statements of Pythagoras's theorem, we should note that as it is used frequently there are many examples of Pythagorean triples in the Sulbasutras. For example (5, 12, 13), (12, 16, 20), (8, 15, 17), (15, 20, 25), (12, 35, 37), (15, 36, 39), (, 6, ), and (, 10, ) all occur.
Now the Sulbasutras are really construction manuals for geometric shapes such as squares, circles, rectangles, etc. and we illustrate this with some examples.
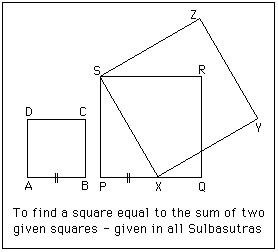
The first construction we examine occurs in most of the different Sulbasutras. It is a construction, based on Pythagoras's theorem, for making a square equal in area to two given unequal squares.
Consider the diagram on the right.
and are the two given squares. Mark a point on so that is equal to . Then the square on has area equal to the sum of the areas of the squares and . This follows from Pythagoras's theorem since .
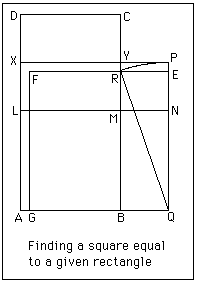
The next construction which we examine is that to find a square equal in area to a given rectangle. We give the version as it appears in the Baudhayana Sulbasutra.
Consider the diagram on the right.
The rectangle is given. Let be marked on so that . Then complete the square . Now bisect at and divide the rectangle into two equal rectangles with the line . Now move the rectangle to the position . Complete the square .
Now the square we have just constructed is not the one we require and a little more work is needed to complete the work. Rotate about so that it touches at . Then and we see that this is an ideal "rope" construction. Now draw parallel to and complete the square . This is the required square equal to the given rectangle .
The Baudhayana Sulbasutra offers no proof of this result (or any other for that matter) but we can see that it is true by using Pythagoras's theorem.
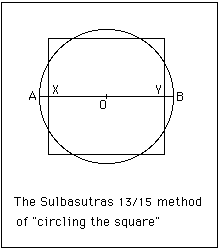 All the Sulbasutras contain a method to square the circle. It is an approximate method based on constructing a square of side times the diameter of the given circle as in the diagram on the right. This corresponds to taking so it is not a very good approximation and certainly not as good as was known earlier to the Babylonians.
All the Sulbasutras contain a method to square the circle. It is an approximate method based on constructing a square of side times the diameter of the given circle as in the diagram on the right. This corresponds to taking so it is not a very good approximation and certainly not as good as was known earlier to the Babylonians.
It is worth noting that many different values of π appear in the Sulbasutras, even several different ones in the same text. This is not surprising for whenever an approximate construction is given some value of π is implied. The authors thought in terms of approximate constructions, not in terms of exact constructions with π but only having an approximate value for it. For example in the Baudhayana Sulbasutra, as well as the value of , there appears and . In different Sulbasutras the values 2.99, 3.00, 3.004, 3.029, 3.047, 3.088, 3.1141, 3.16049 and 3.2022 can all be found; see [6]. In [3] the value is found in the Manava Sulbasutras.
In [9] in addition to examining the problem of squaring the circle as given by Apastamba, the authors examine the problem of dividing a segment into seven equal parts which occurs in the same Sulbasutra.
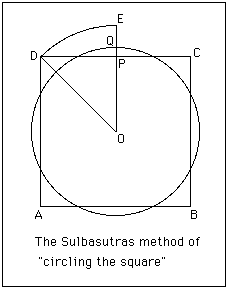
The Sulbasutras also examine the converse problem of finding a circle equal in area to a given square.
Consider the diagram on the right.
The following construction appears. Given a square find the centre . Rotate to position where passes through the midpoint of the side of the square . Let be the point on such that is one third of . The required circle has centre and radius .
Again it is worth calculating what value of π this implies to get a feel for how accurate the construction is. Now if the square has side then the radius of the circle is where
which gives .
As a final look at the mathematics of the Sulbasutras we examine what may be the most remarkable. Both the Apastamba Sulbasutra and the Katyayana Sulbasutra give the following approximation to :-
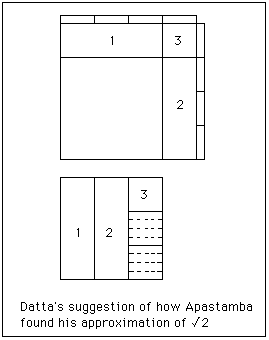
In [1] Datta considers a diagram similar to the one on the right.
The most likely reason for the construction was to build an altar twice the size of one already built. Datta's suggestion involves taking two squares and cutting up the second square and assembling it around the first square to give a square twice the size, thus having side . The second square is cut into three equal strips, and strips 1 and 2 placed around the first square as indicated in the diagram. The third strip has a square cut off the top and placed in position 3. We now have a new square but some of the second square remains and still has to be assembled around the first.
Cut the remaining parts (two-thirds of a strip) into eight equal strips and arrange them around the square we are constructing as in the diagram. We have now used all the parts of the second square but the new figure we have constructed is not quite a square having a small square corner missing. It is worth seeing what the side of this "not quite a square" is. It is
Of course we have still made an approximation since the two strips of breadth which we cut off overlapped by a square of side in the bottom left hand corner. If we had taken this into account we would have obtained the equation
In [4] Gupta gives a simpler way of obtaining the approximation for than that given by Datta in [1]. He uses linear interpolation to obtain the first two terms, he then corrects the two terms so obtaining the third term, then correcting the three terms obtaining the fourth term. Although the method given by Gupta is simpler (and an interesting contribution) there is certainly something appealing in Datta's argument and somehow a feeling that this is in the spirit of the Sulbasutras.
Of course the method used by these mathematicians is very important to understanding the depth of mathematics being produced in India in the middle of the first millennium BC. If we follow the suggestion of some historians that the writers of the Sulbasutras were merely copying an approximation already known to the Babylonians then we might come to the conclusion that Indian mathematics of this period was far less advanced than if we follow Datta's suggestion.
The Sulbasutras are appendices to the Vedas which give rules for constructing altars. If the ritual sacrifice was to be successful then the altar had to conform to very precise measurements. The people made sacrifices to their gods so that the gods might be pleased and give the people plenty food, good fortune, good health, long life, and lots of other material benefits. For the gods to be pleased everything had to be carried out with a very precise formula, so mathematical accuracy was seen to be of the utmost importance. We should also note that there were two types of sacrificial rites, one being a large public gathering while the other was a small family affair. Different types of altars were necessary for the two different types of ceremony.
All that is known of Vedic mathematics is contained in the Sulbasutras. This in itself gives us a problem, for we do not know if these people undertook mathematical investigations for their own sake, as for example the ancient Greeks did, or whether they only studied mathematics to solve problems necessary for their religious rites. Some historians have argued that mathematics, in particular geometry, must have also existed to support astronomical work being undertaken around the same period.
Certainly the Sulbasutras do not contain any proofs of the rules which they describe. Some of the rules, such as the method of constructing a square of area equal to a given rectangle, are exact. Others, such as constructing a square of area equal to that of a given circle, are approximations. We shall look at both of these examples below but the point we wish to make here is that the Sulbasutras make no distinction between the two. Did the writers of the Sulbasutras know which methods were exact and which were approximations?
The Sulbasutras were written by a scribe, although he was not the type of scribe who merely makes a copy of an existing document but one who put in considerable content and all the mathematical results may have been due to these scribes. We know nothing of the men who wrote the Sulbasutras other than their names and a rough indication of the period in which they lived. Like many ancient mathematicians our only knowledge of them is their writings. The most important of these documents are the Baudhayana Sulbasutra written about 800 BC and the Apastamba Sulbasutra written about 600 BC. Historians of mathematics have also studied and written about other Sulbasutras of lesser importance such as the Manava Sulbasutra written about 750 BC and the Katyayana Sulbasutra written about 200 BC.
Let us now examine some of the mathematics contained within the Sulbasutras. The first result which was clearly known to the authors is Pythagoras's theorem. The Baudhayana Sulbasutra gives only a special case of the theorem explicitly:-
The rope which is stretched across the diagonal of a square produces an area double the size of the original square.The Katyayana Sulbasutra however, gives a more general version:-
The rope which is stretched along the length of the diagonal of a rectangle produces an area which the vertical and horizontal sides make together.

The diagram on the right illustrates this result.
Note here that the results are stated in terms of "ropes". In fact, although sulbasutras originally meant rules governing religious rites, sutras came to mean a rope for measuring an altar. While thinking of explicit statements of Pythagoras's theorem, we should note that as it is used frequently there are many examples of Pythagorean triples in the Sulbasutras. For example (5, 12, 13), (12, 16, 20), (8, 15, 17), (15, 20, 25), (12, 35, 37), (15, 36, 39), (, 6, ), and (, 10, ) all occur.
Now the Sulbasutras are really construction manuals for geometric shapes such as squares, circles, rectangles, etc. and we illustrate this with some examples.

The first construction we examine occurs in most of the different Sulbasutras. It is a construction, based on Pythagoras's theorem, for making a square equal in area to two given unequal squares.
Consider the diagram on the right.
and are the two given squares. Mark a point on so that is equal to . Then the square on has area equal to the sum of the areas of the squares and . This follows from Pythagoras's theorem since .

The next construction which we examine is that to find a square equal in area to a given rectangle. We give the version as it appears in the Baudhayana Sulbasutra.
Consider the diagram on the right.
The rectangle is given. Let be marked on so that . Then complete the square . Now bisect at and divide the rectangle into two equal rectangles with the line . Now move the rectangle to the position . Complete the square .
Now the square we have just constructed is not the one we require and a little more work is needed to complete the work. Rotate about so that it touches at . Then and we see that this is an ideal "rope" construction. Now draw parallel to and complete the square . This is the required square equal to the given rectangle .
The Baudhayana Sulbasutra offers no proof of this result (or any other for that matter) but we can see that it is true by using Pythagoras's theorem.
 All the Sulbasutras contain a method to square the circle. It is an approximate method based on constructing a square of side times the diameter of the given circle as in the diagram on the right. This corresponds to taking so it is not a very good approximation and certainly not as good as was known earlier to the Babylonians.
All the Sulbasutras contain a method to square the circle. It is an approximate method based on constructing a square of side times the diameter of the given circle as in the diagram on the right. This corresponds to taking so it is not a very good approximation and certainly not as good as was known earlier to the Babylonians.
It is worth noting that many different values of π appear in the Sulbasutras, even several different ones in the same text. This is not surprising for whenever an approximate construction is given some value of π is implied. The authors thought in terms of approximate constructions, not in terms of exact constructions with π but only having an approximate value for it. For example in the Baudhayana Sulbasutra, as well as the value of , there appears and . In different Sulbasutras the values 2.99, 3.00, 3.004, 3.029, 3.047, 3.088, 3.1141, 3.16049 and 3.2022 can all be found; see [6]. In [3] the value is found in the Manava Sulbasutras.
In [9] in addition to examining the problem of squaring the circle as given by Apastamba, the authors examine the problem of dividing a segment into seven equal parts which occurs in the same Sulbasutra.

The Sulbasutras also examine the converse problem of finding a circle equal in area to a given square.
Consider the diagram on the right.
The following construction appears. Given a square find the centre . Rotate to position where passes through the midpoint of the side of the square . Let be the point on such that is one third of . The required circle has centre and radius .
Again it is worth calculating what value of π this implies to get a feel for how accurate the construction is. Now if the square has side then the radius of the circle is where
Then
which gives .
As a final look at the mathematics of the Sulbasutras we examine what may be the most remarkable. Both the Apastamba Sulbasutra and the Katyayana Sulbasutra give the following approximation to :-
Increase a unit length by its third and this third by its own fourth less the thirty-fourth part of that fourth.Now this gives
which is, to nine places, 1.414215686. Compare the correct value √2 = 1.414213562 to see that the Apastamba Sulbasutra has the answer correct to five decimal places. Of course no indication is given as to how the authors of the Sulbasutras achieved this remarkable result. Datta, in 1932, made a beautiful suggestion as to how this approximation may have been reached.

In [1] Datta considers a diagram similar to the one on the right.
The most likely reason for the construction was to build an altar twice the size of one already built. Datta's suggestion involves taking two squares and cutting up the second square and assembling it around the first square to give a square twice the size, thus having side . The second square is cut into three equal strips, and strips 1 and 2 placed around the first square as indicated in the diagram. The third strip has a square cut off the top and placed in position 3. We now have a new square but some of the second square remains and still has to be assembled around the first.
Cut the remaining parts (two-thirds of a strip) into eight equal strips and arrange them around the square we are constructing as in the diagram. We have now used all the parts of the second square but the new figure we have constructed is not quite a square having a small square corner missing. It is worth seeing what the side of this "not quite a square" is. It is
which, of course, is the first three terms of the approximation. Now Datta argues in [1] that to improve the "not quite a square" the Sulbasutra authors could have calculated how broad a strip one needs to cut off the left hand side and bottom to fill in the missing part which has area . If is the width one cuts off then
.
This has the solution which is approximately 0.002450980392. We now have a square the length of whose sides is
which is exactly the approximation given by the Apastamba Sulbasutra.
Of course we have still made an approximation since the two strips of breadth which we cut off overlapped by a square of side in the bottom left hand corner. If we had taken this into account we would have obtained the equation
for which leads to which is approximately equal to 0.002453105. Of course we cannot take this route since we have arrived back at a value for which involves √2 which is the quantity we are trying to approximate!
In [4] Gupta gives a simpler way of obtaining the approximation for than that given by Datta in [1]. He uses linear interpolation to obtain the first two terms, he then corrects the two terms so obtaining the third term, then correcting the three terms obtaining the fourth term. Although the method given by Gupta is simpler (and an interesting contribution) there is certainly something appealing in Datta's argument and somehow a feeling that this is in the spirit of the Sulbasutras.
Of course the method used by these mathematicians is very important to understanding the depth of mathematics being produced in India in the middle of the first millennium BC. If we follow the suggestion of some historians that the writers of the Sulbasutras were merely copying an approximation already known to the Babylonians then we might come to the conclusion that Indian mathematics of this period was far less advanced than if we follow Datta's suggestion.
References (show)
- B Datta, The science of the Sulba (Calcutta, 1932).
- G G Joseph, The crest of the peacock (London, 1991).
- R C Gupta, New Indian values of π from the Manava sulba sutra, Centaurus 31 (2) (1988), 114-125.
- R C Gupta, Baudhayana's value of √2, Math. Education 6 (1972), B77-B79.
- S C Kak, Three old Indian values of π, Indian J. Hist. Sci. 32 (4) (1997), 307-314.
- R P Kulkarni, The value of π known to Sulbasutrakaras, Indian J. Hist. Sci. 13 (1) (1978), 32-41.
- G Kumari, Some significant results of algebra of pre-Aryabhata era, Math. Ed. (Siwan) 14 (1) (1980), B5-B13.
- A Mukhopadhyay and M R Adhikari, The concept of cyclic quadrilaterals : its origin and development in India (from the age of Sulba Sutras to Bhaskara I, Indian J. Hist. Sci. 32 (1) (1997), 53-68.
- A E Raik and V N Ilin, A reconstruction of the solution of certain problems from the Apastamba Sulbasutra of Apastamba (Russian), in A P Juskevic, S S Demidov, F A Medvedev and E I Slavutin, Studies in the history of mathematics 19 "Nauka" (Moscow, 1974), 220-222; 302.
Written by J J O'Connor and E F Robertson
Last Update November 2000
Last Update November 2000