The Ten Mathematical Classics
The Sui dynasty was short lived, lasting from 581 to 618, but it was important in unifying a country which had been divided for over 300 years. Education became important and mathematics was taught at the Imperial Academy. The T'ang dynasty, which followed the Sui dynasty, continued the educational development which had already begun and formalised the teaching of mathematics. The History of the T'ang records (see [1]):-
Let us look briefly at the contents of the texts.
1. Zhoubi suanjing (Zhou Shadow Gauge Manual)
This was essentially an astronomy text, thought to have been compiled between 100 BC and 100 AD, containing some important mathematical sections. The text measures the positions of the heavenly bodies using shadow gauges which are also called gnomons. How a gnomon might be used is described in a conversation in the text:-
Perhaps the most important mathematics which is included in the Zhoubi suanjing is related to the Gougu rule, which is the Chinese version of the Pythagoras Theorem.
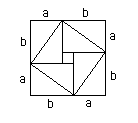
The big square has area . The four "corner" triangles each have area giving a total area of for the four added together. Hence the inside square (whose vertices are on the outside square) has area
The author of the Zhoubi suanjing writes that Emperor Yu:-
2. Jiuzhang suanshu (Nine Chapters on the Mathematical Art)
This is the most important of all the texts included in the Ten Mathematical Classics, but there is no need to discuss it in the article since our archive contains a separate article on The Nine Chapters on the Mathematical Art.
3. Haidao suanjing (Sea Island Mathematical Manual)
This text was written by Liu Hui in 263 AD. This is a small work consisting of nine problems and it was originally written as part of his commentary on Chapter Nine of The Nine Chapters on the Mathematical Art but later removed and made into a separate work by Li Chunfeng and his colleagues during the creation of The Ten Mathematical Classics. A translation of the Haidao suanjing appears in [3]
The Haidao suanjing shows how to use the Gougu theorem (Pythagoras theorem) to calculate heights of objects and distances to objects which cannot be measured directly. The first problem, which illustrates the style, concerns the height and distance to an island in the sea. It gives its name to the book.
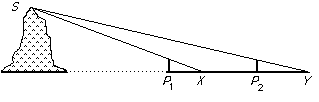
and are poles 5 pu high and 1000 pu apart. When viewed from X at ground level, 123 pu behind , the summit of the island is in line with the top of . Similarly when viewed from Y at ground level, 127 pu behind , the top of the island is in line with the top of . Calculate the height of the island and its distance from .
[Note: 1 pu is about 2 metres.]
Li Chunfeng and his colleagues added a commentary which begins:-
He then gives: height of the island: 1255 pu; distance from to the island: 30750 pu.
Other problems in this work are the height of a tree on the side of a mountain, the distance to a square town, the depth of a gorge, the height of a tower on a hill, the width of a river, the depth of a valley with a lake at the bottom, the width of a ford viewed from a hill, and the size of a town seen from a mountain.
4. Sunzi suanjing (Sun Zi's Mathematical Manual)
Historians have given a wide variety of dates for this text but Wang Ling [4] seems to have the most convincing argument:-
The Sunzi suanjing consists of three chapters, the first describing systems of measuring with considerable detail on using counting rods to multiply, divide, and compute square roots. The second and third chapters consist of problems (28 and 36 respectively) concerning fractions, areas, volumes etc. similar to, but rather easier than, the problems in the Nine Chapters on the Mathematical Art One problem, however, is of special interest, this being Problem 26 in Chapter 3:-
This text is clearly designed for the teaching those entering the five government departments set up in the Sui district around 220 and which lasted until 581; the text is probably from the fifth century. The five departments were Agriculture, War, Accounts, Granary, and Treasury and there is a chapter relating to each. The main interest in this text is that although many of the 19 formulas given to find the areas of different shapes of fields in the first chapter give approximately the right answer, they are actually incorrect. This motivated later mathematical work.
6. Xiahou Yang suanjing (Xiahou Yang's Mathematical Manual)
This text contains three chapters containing 19, 29 and 44 problems respectively. None of the problems presents anything new.
7. Zhang Qiujian suanjing (Zhang Qiujian's Mathematical Manual)
Another work of three chapters with 15, 22 and 38 problems respectively. There are problems on the least common multiple and arithmetic progressions.
8. Wujing suanshu (Arithmetic methods in the Five Classics)
A slightly strange work which contains a commentary on specific parts of five non-mathematical texts. The commentary does contain mathematics, particularly relating to questions concerning the calendar and large numbers.
9. Jigu suanjing (Continuation of Ancient Mathematics)
We do know the author of this work, namely Wang Xiaotong. It is a strange mixture of practical problems arising in the construction of dykes and canals with fanciful problems which would not arise in practice. Sometime, strangely, problems contain both aspects.
10. Shushu jiyi (Notes on Traditions of Arithmetic Methods)
The author of this text is claimed to be Xu Yue and to have been written at the beginning of the third century. This is unlikely and almost certainly a later author trying to claim a certain respectability for his writings. It is a difficult work to understand, in part showing how very large numbers can be constructed using powers of ten. The author may have had in mind convincing his reader that it was possible to express arbitrarily large numbers. Parts of the text seem to have more religious content than mathematical.
11. Zhui shu (Method of Interpolation)
This book was written by Zu Chongzhi (sometimes written Tsu Ch'ung Chi). He was an outstanding mathematician but sadly the text of the Zhui shu has not survived. It is known that Zu Chongzhi found the very good approximation to π, namely , and it is thought that this book used clever methods to find areas and volumes using limiting processes. Zu Chongzhi seems to have been the first Chinese mathematician to compute correctly the volume of a sphere. The Zhui shu was too advanced for the students at the Imperial Academy and it was dropped from the syllabus for that reason. This almost certainly explains why the text has not survived.
12. Sandeng shu (Art of the Three Degrees; Notation of Large Numbers)
This book was written by Dong Quan.
The astronomical observer Wang Sibian presented a memoir to the emperor reporting that the ten mathematical texts such as the Wucao suanjing or the Sunzi suanjing were riddled with mistakes and contradictions. As a consequence Li Chunfeng together with Liang Shu, an expert in mathematics from the ministry of education, and Wang Zhenru, a teacher from the national university and others were ordered by imperial decree to annotate the ten mathematical texts such as the Wucao suanjing or the Sunzi suanjing. Once their task was completed the Emperor Kao-tsu ordered that these books be used at the National University.The first T'ang emperor Li Yüan was known by his temple name Kao-tsu and ruled from 618 to 626. This allows us to date the start of the work by Li Chunfeng and his colleagues fairly accurately. Although called The Ten Mathematical Classics by later writers, there were more than ten books in the collection assembled by Li Chunfeng. The works were:
- Zhoubi suanjing (Zhou Shadow Gauge Manual)
- Jiuzhang suanshu (Nine Chapters on the Mathematical Art)
- Haidao suanjing (Sea Island Mathematical Manual)
- Sunzi suanjing (Sun Zi's Mathematical Manual)
- Wucao suanjing (Mathematical Manual of the Five Administrative Departments)
- Xiahou Yang suanjing (Xiahou Yang's Mathematical Manual)
- Zhang Qiujian suanjing (Zhang Qiujian's Mathematical Manual)
- Wujing suanshu (Arithmetic methods in the Five Classics)
- Jigu suanjing (Continuation of Ancient Mathematics)
- Shushu jiyi (Notes on Traditions of Arithmetic Methods)
- Zhui shu (Method of Interpolation)
- Sandeng shu (Art of the Three Degrees; Notation of Large Numbers)
Let us look briefly at the contents of the texts.
1. Zhoubi suanjing (Zhou Shadow Gauge Manual)
This was essentially an astronomy text, thought to have been compiled between 100 BC and 100 AD, containing some important mathematical sections. The text measures the positions of the heavenly bodies using shadow gauges which are also called gnomons. How a gnomon might be used is described in a conversation in the text:-
Duke of Zhu: How great is the art of numbers? Tell me something about the application of the gnomon.The Zhoubi suanjing contains calculations of the movement of the sun through the year as well as observations of the moon and stars, particularly the pole star.
Shang Gao: Level up one leg of the gnomon and use the other leg as a plumb line. When the gnomon is turned up, it can measure height; when it is turned over, it can measure depth and when it lies horizontally it can measure distance. Revolve the gnomon about its vertex and it can draw a circle; combine two gnomons and they form a square.
Perhaps the most important mathematics which is included in the Zhoubi suanjing is related to the Gougu rule, which is the Chinese version of the Pythagoras Theorem.

The big square has area . The four "corner" triangles each have area giving a total area of for the four added together. Hence the inside square (whose vertices are on the outside square) has area
.
Its side therefore has length . Therefore the hypotenuse of the right angled triangle with sides of length and has length .
The author of the Zhoubi suanjing writes that Emperor Yu:-
... quells floods, deepens rivers and streams, surveys high places and low places by using the Gougu rule.This emphasises its practical use in surveying. However, the text of the Zhoubi suanjing also explains that the reason that mathematics can be applied to so many different cases is as a result of the way that mathematical reasoning allows one to pass from particular to general situations. This realisation of the abstract nature of mathematics is important.
2. Jiuzhang suanshu (Nine Chapters on the Mathematical Art)
This is the most important of all the texts included in the Ten Mathematical Classics, but there is no need to discuss it in the article since our archive contains a separate article on The Nine Chapters on the Mathematical Art.
3. Haidao suanjing (Sea Island Mathematical Manual)
This text was written by Liu Hui in 263 AD. This is a small work consisting of nine problems and it was originally written as part of his commentary on Chapter Nine of The Nine Chapters on the Mathematical Art but later removed and made into a separate work by Li Chunfeng and his colleagues during the creation of The Ten Mathematical Classics. A translation of the Haidao suanjing appears in [3]
The Haidao suanjing shows how to use the Gougu theorem (Pythagoras theorem) to calculate heights of objects and distances to objects which cannot be measured directly. The first problem, which illustrates the style, concerns the height and distance to an island in the sea. It gives its name to the book.

and are poles 5 pu high and 1000 pu apart. When viewed from X at ground level, 123 pu behind , the summit of the island is in line with the top of . Similarly when viewed from Y at ground level, 127 pu behind , the top of the island is in line with the top of . Calculate the height of the island and its distance from .
[Note: 1 pu is about 2 metres.]
Li Chunfeng and his colleagues added a commentary which begins:-
Here the summit of the island refers to the top of a hill. Poles are the tips of vertically standing rods. The line of sight passes through the tip of the pole and the summit of the island. ...Suppose the poles are of height and the distance between the poles is . Liu Hui gives the height of the island as and the distance to it to be .
He then gives: height of the island: 1255 pu; distance from to the island: 30750 pu.
Other problems in this work are the height of a tree on the side of a mountain, the distance to a square town, the depth of a gorge, the height of a tower on a hill, the width of a river, the depth of a valley with a lake at the bottom, the width of a ford viewed from a hill, and the size of a town seen from a mountain.
4. Sunzi suanjing (Sun Zi's Mathematical Manual)
Historians have given a wide variety of dates for this text but Wang Ling [4] seems to have the most convincing argument:-
The Sunzi suanjing mentions the mein as an item of taxation, and the hu tiao system. these two were first established in 280 AD. So the book could not have been written before this date. ... A new scale between chih and tuan was established in 474 AD; the Sunzi, still using the old scale by Wu Ch'en-Shih's emendation, cannot be older than 473 AD.Of course this dating assumes that the text was written as a whole, while it seems more likely that it was compiled, like many of the texts, from older sources. In that case Wang Ling's dating will only establish when part of the text was written, some possibly being earlier, while other parts probably have been written later.
The Sunzi suanjing consists of three chapters, the first describing systems of measuring with considerable detail on using counting rods to multiply, divide, and compute square roots. The second and third chapters consist of problems (28 and 36 respectively) concerning fractions, areas, volumes etc. similar to, but rather easier than, the problems in the Nine Chapters on the Mathematical Art One problem, however, is of special interest, this being Problem 26 in Chapter 3:-
Suppose we have an unknown number of objects. When counted in threes, 2 are left over, when counted in fives, 3 are left over, and when counted in sevens, 2 are left over. How many objects are there?This, of course, is important for it is a problem which is solved using the Chinese remainder theorem. In fact the solution given, although in a special case, gives exactly the modern method. After solving the particular problem (the answer is 23) the Sunzi suanjing gives a method for arbitrary remainders:-
Multiply the number of units left over when counting in threes by 70, add to the product of the number of units left over when counting in fives by 21, and then add the product of the number of units left over when counting in sevens by 15. If the answer is 106 or more then subtract multiples of 105.5. Wucao suanjing (Mathematical Manual of the Five Administrative Departments)
This text is clearly designed for the teaching those entering the five government departments set up in the Sui district around 220 and which lasted until 581; the text is probably from the fifth century. The five departments were Agriculture, War, Accounts, Granary, and Treasury and there is a chapter relating to each. The main interest in this text is that although many of the 19 formulas given to find the areas of different shapes of fields in the first chapter give approximately the right answer, they are actually incorrect. This motivated later mathematical work.
6. Xiahou Yang suanjing (Xiahou Yang's Mathematical Manual)
This text contains three chapters containing 19, 29 and 44 problems respectively. None of the problems presents anything new.
7. Zhang Qiujian suanjing (Zhang Qiujian's Mathematical Manual)
Another work of three chapters with 15, 22 and 38 problems respectively. There are problems on the least common multiple and arithmetic progressions.
8. Wujing suanshu (Arithmetic methods in the Five Classics)
A slightly strange work which contains a commentary on specific parts of five non-mathematical texts. The commentary does contain mathematics, particularly relating to questions concerning the calendar and large numbers.
9. Jigu suanjing (Continuation of Ancient Mathematics)
We do know the author of this work, namely Wang Xiaotong. It is a strange mixture of practical problems arising in the construction of dykes and canals with fanciful problems which would not arise in practice. Sometime, strangely, problems contain both aspects.
10. Shushu jiyi (Notes on Traditions of Arithmetic Methods)
The author of this text is claimed to be Xu Yue and to have been written at the beginning of the third century. This is unlikely and almost certainly a later author trying to claim a certain respectability for his writings. It is a difficult work to understand, in part showing how very large numbers can be constructed using powers of ten. The author may have had in mind convincing his reader that it was possible to express arbitrarily large numbers. Parts of the text seem to have more religious content than mathematical.
11. Zhui shu (Method of Interpolation)
This book was written by Zu Chongzhi (sometimes written Tsu Ch'ung Chi). He was an outstanding mathematician but sadly the text of the Zhui shu has not survived. It is known that Zu Chongzhi found the very good approximation to π, namely , and it is thought that this book used clever methods to find areas and volumes using limiting processes. Zu Chongzhi seems to have been the first Chinese mathematician to compute correctly the volume of a sphere. The Zhui shu was too advanced for the students at the Imperial Academy and it was dropped from the syllabus for that reason. This almost certainly explains why the text has not survived.
12. Sandeng shu (Art of the Three Degrees; Notation of Large Numbers)
This book was written by Dong Quan.
References (show)
- J-C Martzloff, A history of Chinese mathematics (Berlin-Heidelberg, 1997).
- J-C Martzloff, Histoire des mathématiques chinoises (Paris, 1987).
- K Shen, J N Crossley and A W-C Lun, The nine chapters on the mathematical art : Companion and commentary (Beijing, 1999).
- L Wang, The date of the Sunzi suanjing and the Chinese remainder theorem, in Proc. Tenth Internat. Conf. History of Science, 1962 (Paris, 1964), 489-492.
Written by J J O'Connor and E F Robertson
Last Update December 2003
Last Update December 2003