Trisecting an angle
There are three classical problems in Greek mathematics which were extremely influential in the development of geometry. These problems were those of squaring the circle, doubling the cube and trisecting an angle. Although these are closely linked, we choose to examine them in separate articles. The present article studies the problem of trisecting an arbitrary angle. In some sense this is the least famous of the three problems. Certainly in ancient Greek times doubling of the cube was the most famous, then in more modern times the problem of squaring the circle became the more famous, especially among amateur mathematicians.
The problem of trisecting an arbitrary angle, which we examine here, is the one for which I [EFR] have been sent the largest number of false proofs during my career. It is an easy task to tell that a 'proof' one has been sent 'showing' that the trisector of an arbitrary angle can be constructed using ruler and compasses must be incorrect since no such construction is possible. Of course knowing that a proof is incorrect and finding the error in it are two different matters and often the error is subtle and hard to find.
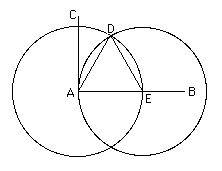
There are a number of ways in which the problem of trisecting an angle differs from the other two classical Greek problems. Firstly it has no real history relating to the way that the problem first came to be studied. Secondly it is a problem of a rather different type. One cannot square any circle, nor can one double any cube. However, it is possible to trisect certain angles. For example there is a fairly straightforward method to trisect a right angle. For given the right angle draw a circle to cut at . Draw a second circle (with the same radius) with centre and let it intersect the first circle at . Then is an equilateral triangle and so the angle is 60° and is 30°. So the angle is trisected.
Perhaps more surprisingly, angles such as one of 27° can be trisected - can you solve this? The problem is therefore to trisect an arbitrary angle and the aim is to make the construction using ruler and compass (which is impossible) but failing that to devise some method to trisect an arbitrary angle.
Pappus in his Mathematical collection writes (see for example [3]):-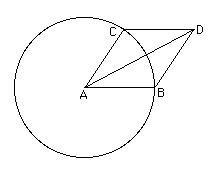
We will describe the methods which were invented to solve this problem in a moment but first of all let us see why this problem arose in a natural way. Perhaps the most obvious way that one would come across the problem would be by examining a ruler and compass construction to bisect an angle. This is straightforward. Given the angle then mark off equal lengths and . Complete the parallelogram and draw in the diagonal which is then easily seen to bisect the angle .
The ancient Greeks would certainly have wanted to divide angles into any required ratio for once that is possible the construction of a regular polygon of any number of sides would become possible. The construction of regular polygons using ruler and compass was certainly one of the major aims of Greek mathematics and it was not until the discoveries of Gauss that further polygons were constructed with ruler and compass which the ancient Greeks had failed to find.
Although it is difficult to give an accurate date as to when the problem of trisecting an angle first appeared, we do know that Hippocrates, who made the first major contribution to the problems of squaring a circle and doubling a cube, also studied the problem of trisecting an angle. There is a fairly straightforward way to trisect any angle which was known to Hippocrates.
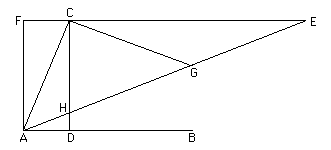
It works as follows. Given an angle then draw perpendicular to to cut it at . Complete the rectangle . Extend to and let be drawn to cut at . Have the point chosen so that . Now angle is of angle .
To see this let be the midpoint of so that = = . Since is a right angle, . Now angle = angle = angle . Also since we have angle = angle . But angle = angle + angle = 2 × = 2 × as required.
Now one of the reasons why the problem of trisecting an angle seems to have attracted less in the way of reported solutions by the best ancient Greek mathematicians is that the construction above, although not possible with an unmarked straight edge and compass, is nevertheless easy to carry out in practice. A mechanical type of solution is easily found. Just mark off a length of at the right hand end of the ruler and then slide the ruler with one mark on , the other on extended until the ruler defines a line passing through . The trisector has then been found by a fairly easy mechanical process. So as a practical problem there was little left to do although the Greeks still were not satisfied in general with mechanical solutions from a purely mathematical point of view they did not find them. As Plato said:-
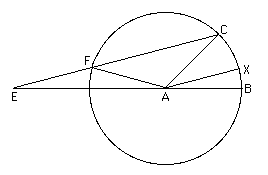
Given an angle draw a circle with centre so that and are radii of the circle. From draw a line to cut produced at . Have this line cut the circle at and have the property that is equal to the radius of the circle. Again this can be done in a mechanical way by marking a length equal to the radius of the circle on the ruler and moving it keeping one mark on produced and having the second mark on the circle. Move the ruler keeping one mark on the line and the other on the circle until the ruler passes through . Then the line is constructed. Finally draw from the radius of the circle with parallel to . Then trisects angle .
This is rather easy to see. Angle = angle = angle = angle + angle = 2 × angle = 2 × angle .
Nicomedes lived at about the same time as Archimedes (in the second century BC) and he produced his famous conchoid curve. In fact this curve was invented by Nicomedes precisely to formalise the process which we have described of rotating a ruler keeping a point on a line. The ruler has a fixed distance marked on it and one mark is kept on a given line while the other traces the conchoid curve. The construction is explained in more detail in Nicomedes' biography in this archive. Now this is exactly the curve needed to solve both versions of trisection of an angle given above and Nicomedes solved the problem with his curve. However, in practice the method of moving a ruler until the required configuration was found was on the whole much easier than drawing the conchoid so Nicomedes method was more of theoretical rather than practical interest. Heath writes in [1]:-
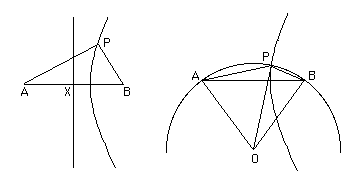
The first shows that if is a fixed line then locus of a point such that 2 × angle = angle is a hyperbola. The hyperbola has eccentricity 2, focus and directrix the perpendicular bisector of . The hyperbola is given in the left of the two diagrams. The right of the two diagrams shows how this hyperbola can be used to trisect the angle . With as centre draw a circle through and . Then construct the parabola with eccentricity 2, focus and directrix the perpendicular bisector of . Let it cut the circle at . Then trisects the angle .
To see this we need to note that, from the property of the hyperbola described above, 2 × angle = angle . But 2 × angle = angle , and 2 × angle = angle (angle at centre of a circle is twice the angle at the circumference standing on the same arc). Hence 2 × angle = angle as required.
Heath comments on how this passage in Pappus is interesting with regard to the Greek development of conics. He writes [1]:-
The proof of the impossibility had to await the mathematics of the 19th century. The final pieces of the argument were put together by Pierre Wantzel. In 1837 Wantzel published proofs in Liouville's Journal of:-
The problem of trisecting an arbitrary angle, which we examine here, is the one for which I [EFR] have been sent the largest number of false proofs during my career. It is an easy task to tell that a 'proof' one has been sent 'showing' that the trisector of an arbitrary angle can be constructed using ruler and compasses must be incorrect since no such construction is possible. Of course knowing that a proof is incorrect and finding the error in it are two different matters and often the error is subtle and hard to find.
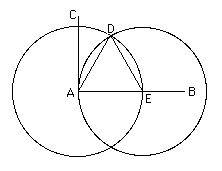
There are a number of ways in which the problem of trisecting an angle differs from the other two classical Greek problems. Firstly it has no real history relating to the way that the problem first came to be studied. Secondly it is a problem of a rather different type. One cannot square any circle, nor can one double any cube. However, it is possible to trisect certain angles. For example there is a fairly straightforward method to trisect a right angle. For given the right angle draw a circle to cut at . Draw a second circle (with the same radius) with centre and let it intersect the first circle at . Then is an equilateral triangle and so the angle is 60° and is 30°. So the angle is trisected.
Perhaps more surprisingly, angles such as one of 27° can be trisected - can you solve this? The problem is therefore to trisect an arbitrary angle and the aim is to make the construction using ruler and compass (which is impossible) but failing that to devise some method to trisect an arbitrary angle.
Pappus in his Mathematical collection writes (see for example [3]):-
When the ancient geometers sought to divide a given rectilinear angle into three equal parts they were at a loss for this reason. We say that there are three kinds of problem in geometry, the so-called 'plane', 'solid', and 'linear' problems. Those that can be solved with straight line and circle are properly called 'plane' problems, for the lines by which such problems are solved have their origin in a plane. Those problems that are solved by the use of one or more sections of the cone are called 'solid' problems. For it is necessary in the construction to use surfaces of solid figures, that is to say, cones. There remain the third type, the so-called 'linear' problem. For the construction in these cases curves other than those already mentioned are required, curves having a more varied and forced origin and arising from more irregular surfaces and from complex motions. Of this character are the curves discovered in the so-called 'surface loci' and numerous others even more involved ... . These curves have many wonderful properties. More recent writers have indeed considered some of them worthy of more extended treatment, and one of the curves is called 'the paradoxical curve' by Menelaus. Other curves of the same type are spirals, quadratrices, cochloids, and cissoids. ... Since problems differ in this way, the earlier geometers were not able to solve the aforementioned problem about the angle, because it is by nature solid; for they were not yet familiar with the sections of the cone, and for that reason were at a loss. Later, however, they trisected the angle by means of the conics, using in the solution the verging described below .....

We will describe the methods which were invented to solve this problem in a moment but first of all let us see why this problem arose in a natural way. Perhaps the most obvious way that one would come across the problem would be by examining a ruler and compass construction to bisect an angle. This is straightforward. Given the angle then mark off equal lengths and . Complete the parallelogram and draw in the diagonal which is then easily seen to bisect the angle .
The ancient Greeks would certainly have wanted to divide angles into any required ratio for once that is possible the construction of a regular polygon of any number of sides would become possible. The construction of regular polygons using ruler and compass was certainly one of the major aims of Greek mathematics and it was not until the discoveries of Gauss that further polygons were constructed with ruler and compass which the ancient Greeks had failed to find.
Although it is difficult to give an accurate date as to when the problem of trisecting an angle first appeared, we do know that Hippocrates, who made the first major contribution to the problems of squaring a circle and doubling a cube, also studied the problem of trisecting an angle. There is a fairly straightforward way to trisect any angle which was known to Hippocrates.

It works as follows. Given an angle then draw perpendicular to to cut it at . Complete the rectangle . Extend to and let be drawn to cut at . Have the point chosen so that . Now angle is of angle .
To see this let be the midpoint of so that = = . Since is a right angle, . Now angle = angle = angle . Also since we have angle = angle . But angle = angle + angle = 2 × = 2 × as required.
Now one of the reasons why the problem of trisecting an angle seems to have attracted less in the way of reported solutions by the best ancient Greek mathematicians is that the construction above, although not possible with an unmarked straight edge and compass, is nevertheless easy to carry out in practice. A mechanical type of solution is easily found. Just mark off a length of at the right hand end of the ruler and then slide the ruler with one mark on , the other on extended until the ruler defines a line passing through . The trisector has then been found by a fairly easy mechanical process. So as a practical problem there was little left to do although the Greeks still were not satisfied in general with mechanical solutions from a purely mathematical point of view they did not find them. As Plato said:-
In proceeding in [a mechanical] way, did not one lose irredeemably the best of geometry...There is another mechanical solution given by Archimedes. Well we should qualify this is little and say that this method is given in the Arabic work called the Book of Lemmas which is attributed to Archimedes. Now certainly this work is not just a translation of a work of Archimedes since Archimedes is quoted several times in the work in a way that is quite impossible for someone to refer to themselves. However, most historians of mathematics believe that many of the results given in the Book of Lemmas are indeed due to Archimedes and the result given on trisecting an angle is so much in the spirit of the work On spirals that it is widely accepted that this method is indeed due to Archimedes. The construction proceeds as follows.

Given an angle draw a circle with centre so that and are radii of the circle. From draw a line to cut produced at . Have this line cut the circle at and have the property that is equal to the radius of the circle. Again this can be done in a mechanical way by marking a length equal to the radius of the circle on the ruler and moving it keeping one mark on produced and having the second mark on the circle. Move the ruler keeping one mark on the line and the other on the circle until the ruler passes through . Then the line is constructed. Finally draw from the radius of the circle with parallel to . Then trisects angle .
This is rather easy to see. Angle = angle = angle = angle + angle = 2 × angle = 2 × angle .
Nicomedes lived at about the same time as Archimedes (in the second century BC) and he produced his famous conchoid curve. In fact this curve was invented by Nicomedes precisely to formalise the process which we have described of rotating a ruler keeping a point on a line. The ruler has a fixed distance marked on it and one mark is kept on a given line while the other traces the conchoid curve. The construction is explained in more detail in Nicomedes' biography in this archive. Now this is exactly the curve needed to solve both versions of trisection of an angle given above and Nicomedes solved the problem with his curve. However, in practice the method of moving a ruler until the required configuration was found was on the whole much easier than drawing the conchoid so Nicomedes method was more of theoretical rather than practical interest. Heath writes in [1]:-
Pappus tells us that in practice the conchoid was not always actually drawn but that some, for greater convenience, moved a ruler about the fixed point until by trial the intercept was found to be equal to the given length.Pappus tell us about the conchoid of Nicomedes in his Mathematical collection (see [3] for example). In the same work Pappus writes about how the problem of trisecting an angle was solved by Apollonius using conics. Pappus gives two solutions which both involve the drawing of a hyperbola.

The first shows that if is a fixed line then locus of a point such that 2 × angle = angle is a hyperbola. The hyperbola has eccentricity 2, focus and directrix the perpendicular bisector of . The hyperbola is given in the left of the two diagrams. The right of the two diagrams shows how this hyperbola can be used to trisect the angle . With as centre draw a circle through and . Then construct the parabola with eccentricity 2, focus and directrix the perpendicular bisector of . Let it cut the circle at . Then trisects the angle .
To see this we need to note that, from the property of the hyperbola described above, 2 × angle = angle . But 2 × angle = angle , and 2 × angle = angle (angle at centre of a circle is twice the angle at the circumference standing on the same arc). Hence 2 × angle = angle as required.
Heath comments on how this passage in Pappus is interesting with regard to the Greek development of conics. He writes [1]:-
The passage from Pappus from which this solution is taken is remarkable as being one of three passages in Greek mathematical works still extant ... which refers to the focus-and-directrix property of conics.These constructions described by Pappus show how the Greeks 'improved' their solutions to the problem of trisecting an angle. From a mechanical solution they had progressed to a solution involving conic sections. They could never progress to plane solutions since we know that such are impossible.
The proof of the impossibility had to await the mathematics of the 19th century. The final pieces of the argument were put together by Pierre Wantzel. In 1837 Wantzel published proofs in Liouville's Journal of:-
... the means of ascertaining whether a geometric problem can be solved with ruler and compasses.Gauss had stated that the problems of doubling a cube and trisecting an angle could not be solved with ruler and compasses but he gave no proofs. In this 1837 paper Wantzel was the first to prove these results. Improved proofs were later given by Charles Sturm but he did not publish them.
References (show)
- T L Heath, A history of Greek mathematics I (Oxford, 1931).
- I Thomas, Selections illustrating the history of Greek mathematics : Vol 1 (From Thales to Euclid) (London, 1967).
- I Thomas, Greek mathematical works (London, 1939).
- Chen, Tzer-lin Proof of the impossibility of trisecting an angle with Euclidean tools, Math. Mag. 39 (1966), 239-241.
- J Delattre and R Bkouche, Why ruler and compass?, in History of Mathematics : History of Problems (Paris, 1997), 89-113.
Written by J J O'Connor and E F Robertson
Last Update April 1999
Last Update April 1999