Henry Frederick Baker was born at Cambridge on 3rd July 1866. He spent his whole life there, living to within 4 months of his 90th birthday.
Baker went into residence at St John's College in October 1884 and was, bracketed with 3 others, Senior Wrangler in 1887. Elected Fellow of St John's in 1888, he remained a Fellow without intermission for 68 years. He won a Smith's Prize in 1889 for an essay on the complete system of 148 concomitants of 3 ternary quadrics. Cayley would doubtless propose the subject; Cayley certainly gave advice on several points before the substance of the essay was published. It shows Baker as an expert manipulator of hyperdeterminants and Clebsch-Aronhold symbols, and as one already well read in the works of the German invariantists. It was thus only natural that J H Grace and Alfred Young should later have recourse to Baker when they began to plan their book on the Algebra of Invariants. Baker threw himself wholeheartedly, after his appointment as College Lecturer in 1890, into the work of lecturing and teaching, of coaching for the Tripos and of supervising research. He was soon propounding problems on double theta-functions, and one of his early students was H E Atkins of Leicester, among the Wranglers of 1893 and later to be British chess champion.
Baker twice went to Göttingen to consult with Felix Klein and there met, among other mathematicians, Hurwitz and Burkhardt. Many years later he would delight in recollecting his taking a walk by invitation with Klein and Gordan, and tell how Frau Klein sent him with her husband to search for coloured eggs under the laurels before breakfast on the morning of Easter Day. Baker had, before going into residence as an undergraduate, enjoyed a trip up the Rhine on a cargo boat, but these Göttingen visits were his last journeys abroad. He married in 1893; his wife, a talented violinist, was delicate and 10 years later he was left a widower with 2 young sons. And although freer to travel abroad again by 1928, when both the Royal Society and Cambridge University appointed him a delegate to the International Congress of Mathematicians at Bologna, he was disinclined to go.
The impetus to visit Göttingen came while he was amassing the material of A [letters and numerals in bold refer to the bibliography at the end], his huge volume on Abelian Functions. Not least among its merits is its use, following Cayley, of matrices to display the periods of abelian integrals and to subject them to linear transformations. Matrices were a tool used effectively by Baker on many occasions. He had attended lectures by the originator of matrices and enjoyed telling how he was, as junior member of an audience of three, obliged to sit opposite Cayley and so be constrained to contemplate the ramifications of the algebra upside down as it evolved under Cayley's hand. On Cayley's right sat J W L Glaisher; on Cayley's left A R Forsyth. One day Cayley enunciated the Cayley-Hamilton Theorem, but proved it for 2-rowed matrices only saying, just as he had written when first publishing the theorem in 1857, that he did not think it necessary to undertake the labour of a formal proof in the general case. Forsyth brought one the next day. And Baker not only heard Cayley talk about matrices; he studied what Frobenius had written about them.
In 1899 Cambridge celebrated Sir George Stokes' 50 years tenure of his professorial chair and Baker contributed 1, a paper on the theory of functions of several complex variables; he followed this in 1903 with 2. The theorem that a function of several variables that has no essential singularity at any finite point can be expressed as a quotient of two integral functions is notable, among other reasons, because an attempt that Weierstrass made to prove it was unsuccessful. Poincaré, however, proved the result for periodic functions by using an expression for the real part of an integral periodic function as a multiple integral. In 1 Baker showed that the imaginary part of the same function was also, expressible as a multiple integral, as therefore was the complete function, and, instigated by another paper of Poincaré's published in 1902, gave in 2, using his result of 1, a simpler method of obtaining Poincaré's solution of Weierstrass' problem. Baker was now an analyst of power. But in the same volume as 2 he published 3, wherein he finds a geometrical property of Weddle's quartic surface - the locus, W say, of vertices of quadric cones through 6 points. These points are nodes of W; the join of any point on W to a node only meets W in a single further point. Each node thus affords an operation of period 2 by which to pass from one point of W to another. Baker demonstrates that the 6 operations are commutative, and deduces that the points, other than those on certain curves, of W fall into closed sets of 32. 3 also contains a geometrical explanation of the known birational correspondence between W and a Kummer surface.
Baker's second book B appeared in 1907 and is more geometrical in tone than A. Some geometry in A there is, notably chapter VI; indeed the subject of abelian functions is, in Baker's view, the parent of all systematic algebraic geometry and appeals frequently to geometrical ideas. But in B one is very conscious of the Kummer and Weddle surfaces which, indeed, dominate chapters III and V. As for the book's title let its author speak for himself, 7 years after its publication. In 8 there occurs this passage.
There are, for any algebraic curve of genus , integrals that are finite everywhere on the corresponding Riemann surface ; these are linearly dependent on among them, and this fact can serve to define - the maximum number of linearly independent integrals. (Throughout the following the single word 'integral' is to be taken as meaning -- everywhere finite integral.') Now can be subjected to a canonical dissection by closed circuits or cycles
The value of an integral round a cycle is a period, so that each integral has periods. The periods of the basic integrals can be displayed in an array of rows and columns, each row corresponding to an integral and each column to a cycle of the dissection; the left-hand square half of the array corresponds to the -cuts, the right-hand half to the -cuts. Now may be such that it is possible to select of the integrals which are linearly independent and such that there is a canonical dissection of for which these integrals all have zero periods except over
It then happens, by a theorem of Poincaré, that there is a complementary system of linearly independent integrals which have zero periods except over
It is important to emphasise that there is no linear dependence between the integrals of one batch and the of the other. The integrals are defective as having less than the, full quota of periods. An elliptic integral, with 2 periods, occurs when .
If the presence of a defective integral causes either or to be 1; whenever a non-singular plane quartic possesses defective integrals one has to be elliptic. This happens when it is possible to choose the triangle of reference so that only even powers of one of the co-ordinates, say of , occur in the equation of . The cubic curve which is the first polar of then splits into and a conic for which and are pole and polar, and has 4 bitangents, concurrent at , whose contacts constitute the set of its intersections with the conic. A general plane quartic does not have any 4 of its bitangents concurrent.
When has an elliptic integral it also has, by Poincaré's theorem, a set of 2 integrals, linearly independent of the elliptic integral and of each other, with 4 periods. For some quartics these 2 integrals can be further broken down, being linearly dependent on 2 elliptic integrals; such a curve has all its integrals linear combinations of 3 elliptic integrals. The possession of defective integrals amplifies geometrical properties; the more defective integrals there are the more interesting is the curve likely to be, and the plane quartics with 3 elliptic integrals are interesting indeed. One of them has 21 elliptic integrals from which a linearly independent set of 3 can be chosen in 14 ways; this curve admits a group of 168 self-collineations and the 14 ways of choosing independent elliptic integrals answer to the 14 octahedral sub-groups. Baker evaluates a set of elliptic integrals for this curve and finds their periods (B p. 266; note also 12). Another curve of great interest in this regard admits a group of 96 self -collineations; its equation can be reduced, in one way only, to and Baker gives (B p. 260) the diagram of a dissection of its 4-sheeted Riemann surface and, on p. 261, evaluates the 3 elliptic integrals. This book indeed has the merit of not confining itself to the general theory; many particular examples are provided to illustrate this theory and throw light upon its difficulties. On p. 272 there appears a curve with which has 3 systems of defective integrals corresponding to the partition 2 + 2 + 5 of 9, and this simply in consequence of its being a plane section of a hyperelliptic surface. The book closes with a description of a curve possessing 5 linearly independent elliptic integrals. is the curve of contact of a Weddle surface W with the tangent cone from one of its nodes and had in fact been encountered in a different guise by Georges Humbert in 1894 and its elliptic integrals recorded. Each node of other than is the vertex of a cubic cone whose generators each meet in 2 points other than , and the elliptic integral on a plane section of the cone is one of those on ; thus each integral is associated with a (2,1) correspondence between and an elliptic curve. Baker gives these geometrical properties of , as well as some of its projection on to a plane from , with explicit forms for the elliptic integrals whether on or on this projection.
Poincaré's theorem on complementary batches of defective integrals dates from 1886; there is a proof, amounting to little more than a piece of matrix algebra, on p. 240 of B. Later, in 1916, Rosati gave a geometrical proof, taking the numbers of a row of the period matrix as homogeneous co-ordinates (A positive integer enclosed in square brackets denotes a linear space of dimensions) in . This Baker took over and gave, with acknowledgment and manifest approbation, at the close of chapter 1 of H.
There is, however, some awkwardness at the end of Rosati's proof, it being essential to verify that there is no linear dependence among the two sets of defective integrals that have emerged or, in the geometrical setting of Rosati's work, that a certain two linear spaces do not meet. Matters might have rested there, but Baker took them up again in 11. This seems to have been prompted by the appearance of Zariski's book in 1935; much work had by then been done in America on Riemann matrices, of which the period matrix is a special instance, and A A Albert had published a purely algebraic proof of Poincaré's theorem (and of the analogous theorem for any Riemann matrix). It seems permissible, reading between the lines of 11, to suspect that Baker was displeased that the American mathematicians had not explicitly alluded to his proof; be that as it may, he is at pains to emphasise the reliance of his argument on matrix theory, and adds an explanation of how his proof of 1907 can be shaped so as to dispense with the a posteriori verification of linear independence at the close of Rosati's proof.
This linear independence of two batches of defective integrals came to have, for Baker, another aspect. He encountered, in the study of algebraic correspondences between two curves, precisely two such batches, on one of the curves, whose independence he strongly suspected but was only able to conjecture. The conjecture was, he showed in 13, equivalent to a lemma of Severi (1905) which was well-known both because of its implications in the theory of Picard integrals on a surface and because there was some hesitation, and not only on Baker's part, in accepting Severi's proof as valid. But just before Baker published 13 Hodge, who saw it in manuscript, succeeded in showing that Baker's conjecture was indeed true. There is an incident relating to this conjecture that is not generally known. In the summer of 1929 Baker was lecturing on these topics and put the conjecture to his class. A few days later he asked for our proof, and showed no little chagrin and disappointment that none of us had found one. Had he tried himself? And, if he had, did he guess that he would have to admit failure 7 years later? And, if he did guess so, would he still have felt entitled to, demand success of his class? Perhaps. He had watched T G Room writing his paper on the double-ten with the pride of a chief architect observing the specification of a new cathedral. He was about to communicate J G Semple's paper, on Cremona Transformations in [4], and H S M Coxeter's, on Polytopes with regular-prismatic vertex figures, to successive volumes of the Philosophical Transactions. These essays were hardly such as to cause him to minimise the capabilities of his pupils. Baker rejoiced in their achievements and they gave him ample cause; a Smith's Prize was won by one of them every year from 1927 to 1933, a run of 7 consecutive prizes: few Cambridge teachers can have had so rewarding an experience. Yet these were the years, immediately subsequent to 1926, that saw legions of researchers and a spate of papers on quantum theory. A new pupil, eager to learn geometry, was always warmly welcomed and Baker's satisfaction was deepened when geometry was chosen in conscious preference to the allurements of the new physical discoveries. But he warned newcomers that discoveries in geometry were unlikely to win recognition whereas "if you go and discover a comet you can write a letter to The Times about it." These same years too were the great years of the Baker tea-party: Saturdays at 4.15 during term: a gathering sui generis if ever any gathering was. Any attempt to describe it would be an attempt to communicate the incommunicable. There one listened to the exposition of the embryonic Smith's Prize essays. Most of us were young, but H W Richmond and F S Macaulay aided Baker to leaven the assembly with the senatorial dignity of years.
The momentum of Poincaré's theorem has thrown this biographical notice forward, and one must now revert to the years following 1907. Here it should be said that Baker edited the 4 volumes of Sylvester's papers, totalling more than 2,800 pages; a task spanning the years 1904-12.
In 1910 appeared 4 wherein the theorem of the double-six is proved, without using the cubic surface through the lines, by purely projective arguments that use only lines and quadrics. It is a paper on which its author set some value since, in his candidature for the Lowndean professorship in December 1913, he singles it out, from among the 43 papers he had by then published, as "evidence of the fact that I have cultivated the constructive methods of the old-established geometry." From 1910, too, dates 5, a paper of over 50 pages concerned with the cubic surface. Most of the treatment here is algebraic; Baker pleads that this is "of advantage to readers not familiar with the matter" and adds that a geometrical treatment is much more attractive, an avowal indicative of his growing predilection for geometry. Early in 1912 came 6, exploiting the fact that every algebraic curve on a cubic surface is expressible as a linear combination of 7 curves, namely one twisted cubic and the lines of one half of a double-six. This has, in its final form, an elementary aspect, but it would not have attained this form unless work of Burnside on groups of linear substitutions had recently become available, while the use of a base of 7 curves stems from Severi's work on algebraic surfaces - a topic that made 1912 a significant year for Baker. The International Congress of Mathematicians met at Cambridge; Baker was one of its organising committee of six and presided at the first meeting of the geometry section on 23rd August. The brief address he then gave is a terse summary of the topics which he speaks of in 7, his masterly Presidential Address, read on 12th December, to the London Mathematical Society. This was hailed by a German reviewer as diese anziehend geschriebenen Darstellung der geschichtlichen Entwicklung der neueren Theorie der algebraischen Oberflächen, and so say all of us. It is a splendid document, the ripeness of the subject for exposition combining most felicitously with the erudition and authority of the expositor. Neither the writing nor the reading of it but would he the better for the prelusion of 4 months earlier when the Italian geometers whose work he was extolling were sitting among his audience. At that congress Baker met, for the only time, Castelnuovo, Enriques and Severi.
In 1913 Baker, a widower for 10 years, married again and brought his bride to North Walsham where he owned a house. He now built the house in Storey's Way, then a private road with gates at either end, and during the building travelled to North Walsham for the week-ends in term. Mrs Baker had been brought up in Norfolk, of which both she and her husband were very fond, and they enjoyed long bicycle rides. They named the new house Walcott, after a hamlet near the Norfolk coast east of North Walsham; it is a house that has meant home to them and much to many people, some of whom will call to mind Belloc's apostrophe:
Baker, while preparing to move into his new home, was appointed to the Lowndean Professorship of Astronomy and Geometry. His claims were very strong, for his publications were voluminous, his erudition profound, and he was now an established teacher of long experience. But some electors might insist on choosing a professor with a knowledge of practical astronomy, and it looks as if they emphatically did. Elections to professorships at Cambridge were presided over by the Vice-Chancellor, who issued the notice of the election on the day the electors met. But Baker's appointment did not conform to this routine - the notice was signed not by the Vice-Chancellor but by the Chancellor, and it was dated not 22nd December 1913, the day that the electors met, but 5th January, 1914. This could be explained by the Vice-Chancellor declining to use a casting vote. Baker's pupils could fittingly make a pilgrimage to Terling Place, Witham, where the Chancellor signed that notice for, in addition to making 5th January 1914 a red-letter day in Baker's life, the appointment has been of immense benefit to the study of geometry at Cambridge and elsewhere. To commemorate our benefactors is a pious duty incumbent on us all, and all who have studied under Baker are eternally indebted to Lord Rayleigh and those who helped to promote Baker to his chair.
These years of the Presidential Address, the second marriage and the appointment to the chair mark a watershed in Baker's life. War supervened, and thereafter Baker was set on the path that he henceforward travelled. His choice of geometry as the dominating intellectual passion of his life is very striking, for he was widely learned and could have been eminent in other branches. He was, after all, of the 19th century and his contemporaries were not prone to specialisation. He lectured on dynamical astronomy almost throughout his tenure of the chair and wrote papers on it as well as on hydrodynamics. In his obituary notice of Poincaré he is every bit as enthusiastic and as well-informed on Poincaré's writings on celestial mechanics as he is on those on automorphic functions and multiply-periodic functions. He proposed the Principle of Least Action for a Smith's Prize essay. Natural Philosophy and its spectacular achievements always captivated him; so close was his long friendship with C T R Wilson that he felt an almost proprietary interest in cloud chambers; he was a friend of P A M Dirac for nigh 30 years and proud that his friendship was reciprocated. But pure mathematics was supreme and, to quote from 8 again, he said publicly
Baker was, as all researchers ought to be, always eager to find things out; he wanted to know. Many were the searching interrogatories to which his pupils were subjected. Let one, whereof the occasion is of no importance, serve as an instance. On 26/4/37 he wrote thus.
An endeavour has been made to point out what are conceived to be the most artistic ways of formally developing the theory regarded as complete.
He would remark on the long process that began with the struggle of the early 19th century French Dynamiker with the axes of permanent rotation of a rigid body, on how these were then recognised as normals of a set of confocal quadrics, which normals, in their turn, were seen to constitute a tetrahedral complex. Each stage, he would insist, was an advance, but the advance was not complete until Corrado Segre announced that the lines of a tetrahedral complex were just the intersections, of the [3] in which they lay, with those planes that meet 3 given lines in a [4]. Another achievement of Segre's was to geometrise Kronecker's results on a pencil of singular quadratic forms. The difficulty of Kronecker's algebraic reduction is notorious but Segre, by equating a singular form to zero and interpreting the equation as a cone in [], where is the number of variables in the form, considers the locus of vertices (which need not be points merely, but spaces of larger dimension) of the cones. As Baker says in 10 :
The striking elucidations by geometry of phenomena that sprang from other branches of mathematics, the sudden perception in a figure of some intrinsic incandescence, these had a profound effect on and a singular fascination for Baker: as though he were being led to recognise the verities of things sub specie aeternitatis. Herein may well have lain the chief reason for his turning to geometry. He so decided, not in the flush of youthful enthusiasm but in the ripening wisdom of mature years. His high appreciation of analysis remained: Riemann he almost worshipped, so impressed was he with the deep insight of his ideas; the work of Weierstrass and Poincaré he knew as few others could know; yet he chose geometry. Amplissima est et pulcherrima scientia figurarum. So he inscribed the title page of the first volume of Principles of Geometry, and so he believed.
The preceding sentences have indicated that a knowledge of geometry in higher space may be necessary for a proper appreciation of geometry in ordinary space, and Baker's main preoccupation in writing F was to publicise this fact; therein Segre's generation of the tetrahedral complex appears on p. 33 while the Kummer surface is found as an apparent contour on p. 156 and closely scrutinised in chapter VII. Cayley, as long ago as 1846, said, after remarking that Desargues' figure in a plane is a projection of the 10 edges and 10 vertices of a pentahedron, that it was only reasonable to expect, by analogy, a simplification of geometry in space by using figures in higher space. Klein, in 1872, explained how geometries in spaces of different dimensions could be equivalent; a geometry does not depend primarily on the ambient space but on the group of self-transformations of the figure. In Cambridge the situation was fully appreciated by H W Richmond, who had exploited it in papers written about 1900. Yet, at home, there seemed no other awareness and Baker would be pondering again the question of his exordium (7): why is it so often the case that the early history in England of a department of Pure Mathematics is a history of importation? He began to unload his cargo.
In 1920 appeared 9, of which Figure 2 is the well-known frontispiece of F; it supersedes 4 wherein the discussion, repeated at the opening of 9, began with 8 lines in [3] whose relation appears artificial because they are not there recorded as being the projection of a completely natural set of 8 lines in [4]. Though F was not to appear for another 5 years it was already being drafted; meanwhile, as harbingers thereof, C, D, E, were duly issued. Nor was it only Baker who so carefully prepared the ground: the lectures and the advocacy of F P White helped to sow in Cambridge the seed for the approaching harvest. Then the volume came: 1925. For all its idiosyncrasies and, one must declare, its anfractuosities of style it is a glorious book, a cornucopia crammed with riches. The cramming is prodigious. A reviewer wrote:
A book of such immense influence cannot be adequately summarised here, yet a fair fraction of this notice must be given to it. Perhaps the best course is to give a full account of a certain equivalence, signalised by Klein and exploited by Segre, between geometries in different spaces, and then indicate a few of the many uses to which Baker puts it.
It may help to describe a metrical example before the projective generalisation. Project a sphere stereographically from its north pole onto its equatorial plane . All circles of become circles in , save that circles through become lines. If, then, we regard lines in as special cases of circles, any circle on either or corresponds to a circle on the other. All this is visually obvious when attention is fixed on real points. But points with complex numbers for their co-ordinates are not visible; there are generating lines lying on , two through each point. Such a pair of generators has a real intersection (the only real point on either) and spans a real plane (the tangent plane of at their intersection). The generators and at span the tangent plane at ; this plane is parallel to so that the intersections of with are at "infinity"; moreover they are "conjugate imaginaries." Not only so: both and meet (at conjugate imaginary points) every real plane section of , and indeed and are Poncelet's pair of points common to every circle in . A line in is amplified to a circle by adding the line .
Plane geometry does not demand that the absolute points be either imaginary or at infinity, as they are in the Euclidean plane. So any non-singular quadric can be projected stereographically from any point of onto any plane not through ; the generators of at meet h in points which can serve as absolute points in the plane geometry. Then all plane sections of S are projected into circles while every circle of so arises from a section of S. Chapter II of F opens thus.
It is not possible, by linear transformation in a plane, to turn lines into circles; but it is possible by inversion. In inversive geometry the lines and circles form a closed family. Klein showed, in the Erlanger Programm of 1872, that inversive geometry in a plane is equivalent to projective geometry on a quadric; this is because, the lines and circles in 7) answering to the plane sections of , it is precisely the plane sections of that must form a closed family in a geometry equivalent to the inversive geometry in h so that must, as a surface, be unaltered and its plane sections permuted among themselves. Inversion in a circle of transposes in pairs those points of which do not lie on while leaving every point of invariant: is the projection from of a section of and the inversion answers to a projectivity in space that transposes in pairs those points of that do not lie on while leaving every point of invariant. This is the projectivity that transposes every pair of points on whose join passes through the pole of the plane of . Hence the projection of the curve of intersection of with any cone whose vertex is is its own inverse in . When this cone is a plane the projection is a circle orthogonal to . When it is a quadric cone the situation is fully explained (p. 96) in Chapter III of F, which opens thus.
The volumes G and H are quite distinct from C, D, E, F. Baker's intention had been to publish a large volume on the theory of algebraic curves and surfaces which would include a topological treatment of the subject in addition to what has now appeared in G and H; but this third part of the volume was not near enough to completion when Baker began to feel, as a man nearing 70 and tiring, that the compilation of the first two-thirds was perhaps as much as he could confidently hope to accomplish. When he retired from his professorship a dinner was given in his honour in St John's College on Saturday, 6th June 1936. On that day the Edinburgh Mathematical Society was meeting in St Andrews and their congratulatory telegram was put into Baker's hand as he entered college.
In 1941 Baker sent the manuscript of I to the press. He was glad to have done this book and set some store by its logical framework, claiming to start absolutely from scratch with no foundations of Euclid's results or of propositions from "sequels" to Euclid, doing the geometry of circles ab initio. He said modestly when it was finished that he did not think highly of many parts of it, but that it might serve as a model for someone some day to make a less imperfect book. It contains an abundance of examples, and a skilled draughtsman with sufficient leisure could fill a large portfolio with handsome diagrams.
When the war ended Baker was near 80, and the fell sergeant had made his preliminary foray. On 20/7/46 Baker wrote:
By the end of 1950 his eyesight was but fitful, and he had to suffer the deprivation of not being able to read on duller days. The cloud of affliction darkened as the last years passed heavily by. In January 1953, he paid the bitter price sometimes exacted for longevity, being predeceased by his younger son. The following December Mrs Baker had to leave home. Pneumonia had hastened the decline of a memory that had begun to fail, and it was essential that she be moved to a nursing home. Baker, though practically confined to his study, was able to make one or two visits by taxi, but it soon became necessary to move her away from Cambridge. The partnership of 40 years was sundered and they never saw one another again. But while these inexorable events could enforce physical separation they could not remove her from his thoughts, and he wrote almost daily. That he felt unable to visit her was a sign of his own awareness of failing strength and, refuse as he might, and for as long as possible, to admit it, his growing realisation that she would not improve (Mrs Baker died on 17th December 1956.) was a potent influence of his own decline. Yet in April 1954, when a colloquium was held in Cambridge, several of his old pupils called to pay their homage and there was no trace in his conversation or demeanour of any resentment or distress. In January 1956 came an onset of phlebitis, while his eyesight by now was poor indeed and, though able to distinguish furniture and large objects, he was quite unable to read. He retained his equanimity throughout and his spirit was still unconquered and undaunted when the end, came peacefully on 17th March.
Baker visited Edinburgh in the first decade of the century, his contemporary F W Dyson being Astronomer Royal for Scotland. An appointment for lunch took him up Blackford Hill, then utterly innocent of suburban contiguity, on a cold winter day in deep snow. The recollection of the stark frigidity of his first climb up that eminence was counterpoised by the warmth of his attachment to it, presided over as it was, from the appointment of Dyson in 1905 till the death of Greaves in 1955, by a personal friend. R A Sampson, who succeeded Dyson in 1910, was 2 years junior to Baker at Cambridge and emulated his friend by winning a Smith's Prize and a St John's Fellowship; this was one of Baker's closest friendships and Sampson was Baker's best man in 1893. But Baker's ties to Scotland were also to other places than Blackford Hill - and other friends than Astronomers Royal. He was an honorary LL.D. of Edinburgh University; he stayed several times with the Whittakers in George Square and had known E T Whittaker and H W Turnbull since their Cambridge days. Turnbull's name is a reminder that Baker's thoughts, when they turned to Scotland, as like as not dwelt longest on the old grey city of St Andrews. He gave courses of lectures there at two colloquia, those of 1926 and 1930. The writer of this notice happened to pay his first call at Walcott in June 1926, and Baker was preparing to leave for St Andrews with Mrs Baker and their daughter in a few days. Twelve years after, on a walk round the Farm, he harked back to this first call and said, with emotion, "Never, never in my life have I enjoyed anything so much as my first visit to St Andrews." At that colloquium H F Baker and H W Richmond used to walk together along the Scores. Those remaining few who beheld that promenade speak about it still, and though the writer did not see it he is able to record it and thereby preserve it from the encroachment of oblivion. Let it be there that we look our last on him, the Cambridge professor savouring the most enjoyable of his too rare holidays, on the meridian of life and at the zenith of happiness, gazing along the West Sands and across the bright estuary to the outline of the Angus hills.
by W L Edge
Baker wrote 10 books, all published by the Cambridge University Press. The dates of the editions are as follows :
A. Abelian Functions 1897
B. Multiply Periodic Functions 1907
Principles of Geometry
C. Foundations 1922, 1929
D. Plane Geometry 1922, 1930
E. Solid Geometry 1923
F. Higher Geometry 1925
G. Theory of Curves 1933
H. Algebraic Surfaces 1933
--------------
I. Introduction to Plane Geometry 1943
J. A locus with 25920 linear self-transformations 1946
The following list of Baker's papers does not include any not referred to in this notice. The list given by Professor Hodge (Biographical Memoirs of Fellows of the Royal Society, Vol. 2) includes 97 papers: a fact that gives some indication of how far, short the above notice falls of an adequate assessment of Baker's work.
1. On the theory of functions of several complex variables.
Trans. Camb. Phil. Soc. 18 (1899), 408.
2. On functions of several variables.
Proc. London Math. Soc.,(2) 1 (1904), 14.
3. Elementary note on the Weddle quartic surface.
Proc. London Math. Soc. (2) 1 (1904), 247.
4. A geometrical proof of the theorem of a double-six of straight lines.
Proc. Royal Soc. (A) 84 (1911), 597.
5. Notes on the theory of the cubic surface.
Proc. London Math. Soc. (2) 9 (1910), 145.
6. On the curves which lie on a cubic surface.
Proc. London Math. Soc. (2) 11 (1912), 285.
7. On some recent advances in the theory of algebraic surfaces.
Proc. London Math. Soc. (2) 12 (1913), 1.
8. The place of pure mathematics.
Nature 92 (1914), 69.
9. On a proof of the theorem of a double-six of lines by projection from four dimensions.
Proc. Camb. Phil. Soc. 20 (1920), 133.
10. Corrado Segre.
Journal London Math. Soc. 1 (1926), 263.
11. On Poincaré's theorem for defective integrals on a Riemann surface.
Journal London Math. Soc. 10 (1935), 281.
12. Note introductory to the study of Klein's group of order 168.
Proc. Camb. Phil. Soc. 31 (1935), 468.
13. On the proof of a lemma enunciated by Severi.
Proc. Camb. Phil. Soc. 32 (1936), 253.
14. On non-commutative algebra, and the foundations of projective geometry.
Proc. Royal Soc. (A) 205 (1951), 178.
15. Note on the foundations of projective geometry.
Proc. Camb. Phil. Soc. 48 (1952), 363.
Baker went into residence at St John's College in October 1884 and was, bracketed with 3 others, Senior Wrangler in 1887. Elected Fellow of St John's in 1888, he remained a Fellow without intermission for 68 years. He won a Smith's Prize in 1889 for an essay on the complete system of 148 concomitants of 3 ternary quadrics. Cayley would doubtless propose the subject; Cayley certainly gave advice on several points before the substance of the essay was published. It shows Baker as an expert manipulator of hyperdeterminants and Clebsch-Aronhold symbols, and as one already well read in the works of the German invariantists. It was thus only natural that J H Grace and Alfred Young should later have recourse to Baker when they began to plan their book on the Algebra of Invariants. Baker threw himself wholeheartedly, after his appointment as College Lecturer in 1890, into the work of lecturing and teaching, of coaching for the Tripos and of supervising research. He was soon propounding problems on double theta-functions, and one of his early students was H E Atkins of Leicester, among the Wranglers of 1893 and later to be British chess champion.
Baker twice went to Göttingen to consult with Felix Klein and there met, among other mathematicians, Hurwitz and Burkhardt. Many years later he would delight in recollecting his taking a walk by invitation with Klein and Gordan, and tell how Frau Klein sent him with her husband to search for coloured eggs under the laurels before breakfast on the morning of Easter Day. Baker had, before going into residence as an undergraduate, enjoyed a trip up the Rhine on a cargo boat, but these Göttingen visits were his last journeys abroad. He married in 1893; his wife, a talented violinist, was delicate and 10 years later he was left a widower with 2 young sons. And although freer to travel abroad again by 1928, when both the Royal Society and Cambridge University appointed him a delegate to the International Congress of Mathematicians at Bologna, he was disinclined to go.
The impetus to visit Göttingen came while he was amassing the material of A [letters and numerals in bold refer to the bibliography at the end], his huge volume on Abelian Functions. Not least among its merits is its use, following Cayley, of matrices to display the periods of abelian integrals and to subject them to linear transformations. Matrices were a tool used effectively by Baker on many occasions. He had attended lectures by the originator of matrices and enjoyed telling how he was, as junior member of an audience of three, obliged to sit opposite Cayley and so be constrained to contemplate the ramifications of the algebra upside down as it evolved under Cayley's hand. On Cayley's right sat J W L Glaisher; on Cayley's left A R Forsyth. One day Cayley enunciated the Cayley-Hamilton Theorem, but proved it for 2-rowed matrices only saying, just as he had written when first publishing the theorem in 1857, that he did not think it necessary to undertake the labour of a formal proof in the general case. Forsyth brought one the next day. And Baker not only heard Cayley talk about matrices; he studied what Frobenius had written about them.
In 1899 Cambridge celebrated Sir George Stokes' 50 years tenure of his professorial chair and Baker contributed 1, a paper on the theory of functions of several complex variables; he followed this in 1903 with 2. The theorem that a function of several variables that has no essential singularity at any finite point can be expressed as a quotient of two integral functions is notable, among other reasons, because an attempt that Weierstrass made to prove it was unsuccessful. Poincaré, however, proved the result for periodic functions by using an expression for the real part of an integral periodic function as a multiple integral. In 1 Baker showed that the imaginary part of the same function was also, expressible as a multiple integral, as therefore was the complete function, and, instigated by another paper of Poincaré's published in 1902, gave in 2, using his result of 1, a simpler method of obtaining Poincaré's solution of Weierstrass' problem. Baker was now an analyst of power. But in the same volume as 2 he published 3, wherein he finds a geometrical property of Weddle's quartic surface - the locus, W say, of vertices of quadric cones through 6 points. These points are nodes of W; the join of any point on W to a node only meets W in a single further point. Each node thus affords an operation of period 2 by which to pass from one point of W to another. Baker demonstrates that the 6 operations are commutative, and deduces that the points, other than those on certain curves, of W fall into closed sets of 32. 3 also contains a geometrical explanation of the known birational correspondence between W and a Kummer surface.
Baker's second book B appeared in 1907 and is more geometrical in tone than A. Some geometry in A there is, notably chapter VI; indeed the subject of abelian functions is, in Baker's view, the parent of all systematic algebraic geometry and appeals frequently to geometrical ideas. But in B one is very conscious of the Kummer and Weddle surfaces which, indeed, dominate chapters III and V. As for the book's title let its author speak for himself, 7 years after its publication. In 8 there occurs this passage.
Our ordinary integral calculus is well-nigh powerless when the result of integration is not expressible by algebraic or logarithmic functions. The attempt to extend the possibilities of integration to the case when the function to, be integrated involves the square root of a polynomial of the fourth order, led first, after many efforts, among which Legendre's devotion of forty years was part, to the theory of doubly-periodic functions. To-day this is much simpler than ordinary trigonometry, and, even apart from its applications, it is quite incredible that it should ever again pass from being among the treasures of civilised man. Then, at first in uncouth form, but now clothed with delicate beauty, came the theory of general algebraic integrals, of which the influence is spread far and wide; and with it all that is systematic in the theory of plane curves, and that is associated with the conception of a Riemann surface. After this came the theory of multiply-periodic functions of any number of variables, which, though still very far indeed from being complete, has, I have always felt, a majesty of conception which is unique.One of the main features of the second part of B is a proof that the most general one-valued multiply-periodic meromorphic function is expressible in terms of theta functions. The proof leans heavily on work of Kronecker on how to define an algebraic construct by systems of equations; but it also uses defective integrals, and before considering Baker's later work as a geometer these should be described in some detail. For they are, as will be seen, close to geometrical concepts; they always occur when there is an algebraic correspondence other than a (1,1) correspondence between two curves, and a curve can often be precisely characterised by some geometrical property when defective integrals occur on it. Baker attached much importance to these integrals which, he contended, were not, in 1907, appreciated as they should have been.
There are, for any algebraic curve of genus , integrals that are finite everywhere on the corresponding Riemann surface ; these are linearly dependent on among them, and this fact can serve to define - the maximum number of linearly independent integrals. (Throughout the following the single word 'integral' is to be taken as meaning -- everywhere finite integral.') Now can be subjected to a canonical dissection by closed circuits or cycles
no cycle meets any other save the one with the same suffix, while and have, for each , a single intersection. remains a connected surface after the cuts are made, but is the maximum number of closed cuts that can be made on without it falling into separate pieces. This connectivity of also serves to define . It is easy to visualise the dissection, starting with when can be a torus, or anchor-ring, generated by the revolution of a circle round a line in its plane that does not meet it. The curves and that dissect the torus are, for , one position of the generating circle and, for , the path traced, through the revolution, by a point on . For take a sphere with holes in it and attach, by a short tube, a torus to each hole; then dissect each torus by the above rule. There is no need for the sphere when since it can then be shrunk on to the surface of the torus; but if this shrinking is prevented by the other holes.
The value of an integral round a cycle is a period, so that each integral has periods. The periods of the basic integrals can be displayed in an array of rows and columns, each row corresponding to an integral and each column to a cycle of the dissection; the left-hand square half of the array corresponds to the -cuts, the right-hand half to the -cuts. Now may be such that it is possible to select of the integrals which are linearly independent and such that there is a canonical dissection of for which these integrals all have zero periods except over
that is, the matrix has the shape

It then happens, by a theorem of Poincaré, that there is a complementary system of linearly independent integrals which have zero periods except over
.
The period matrix thus has the form

It is important to emphasise that there is no linear dependence between the integrals of one batch and the of the other. The integrals are defective as having less than the, full quota of periods. An elliptic integral, with 2 periods, occurs when .
If the presence of a defective integral causes either or to be 1; whenever a non-singular plane quartic possesses defective integrals one has to be elliptic. This happens when it is possible to choose the triangle of reference so that only even powers of one of the co-ordinates, say of , occur in the equation of . The cubic curve which is the first polar of then splits into and a conic for which and are pole and polar, and has 4 bitangents, concurrent at , whose contacts constitute the set of its intersections with the conic. A general plane quartic does not have any 4 of its bitangents concurrent.
When has an elliptic integral it also has, by Poincaré's theorem, a set of 2 integrals, linearly independent of the elliptic integral and of each other, with 4 periods. For some quartics these 2 integrals can be further broken down, being linearly dependent on 2 elliptic integrals; such a curve has all its integrals linear combinations of 3 elliptic integrals. The possession of defective integrals amplifies geometrical properties; the more defective integrals there are the more interesting is the curve likely to be, and the plane quartics with 3 elliptic integrals are interesting indeed. One of them has 21 elliptic integrals from which a linearly independent set of 3 can be chosen in 14 ways; this curve admits a group of 168 self-collineations and the 14 ways of choosing independent elliptic integrals answer to the 14 octahedral sub-groups. Baker evaluates a set of elliptic integrals for this curve and finds their periods (B p. 266; note also 12). Another curve of great interest in this regard admits a group of 96 self -collineations; its equation can be reduced, in one way only, to and Baker gives (B p. 260) the diagram of a dissection of its 4-sheeted Riemann surface and, on p. 261, evaluates the 3 elliptic integrals. This book indeed has the merit of not confining itself to the general theory; many particular examples are provided to illustrate this theory and throw light upon its difficulties. On p. 272 there appears a curve with which has 3 systems of defective integrals corresponding to the partition 2 + 2 + 5 of 9, and this simply in consequence of its being a plane section of a hyperelliptic surface. The book closes with a description of a curve possessing 5 linearly independent elliptic integrals. is the curve of contact of a Weddle surface W with the tangent cone from one of its nodes and had in fact been encountered in a different guise by Georges Humbert in 1894 and its elliptic integrals recorded. Each node of other than is the vertex of a cubic cone whose generators each meet in 2 points other than , and the elliptic integral on a plane section of the cone is one of those on ; thus each integral is associated with a (2,1) correspondence between and an elliptic curve. Baker gives these geometrical properties of , as well as some of its projection on to a plane from , with explicit forms for the elliptic integrals whether on or on this projection.
Poincaré's theorem on complementary batches of defective integrals dates from 1886; there is a proof, amounting to little more than a piece of matrix algebra, on p. 240 of B. Later, in 1916, Rosati gave a geometrical proof, taking the numbers of a row of the period matrix as homogeneous co-ordinates (A positive integer enclosed in square brackets denotes a linear space of dimensions) in . This Baker took over and gave, with acknowledgment and manifest approbation, at the close of chapter 1 of H.
There is, however, some awkwardness at the end of Rosati's proof, it being essential to verify that there is no linear dependence among the two sets of defective integrals that have emerged or, in the geometrical setting of Rosati's work, that a certain two linear spaces do not meet. Matters might have rested there, but Baker took them up again in 11. This seems to have been prompted by the appearance of Zariski's book in 1935; much work had by then been done in America on Riemann matrices, of which the period matrix is a special instance, and A A Albert had published a purely algebraic proof of Poincaré's theorem (and of the analogous theorem for any Riemann matrix). It seems permissible, reading between the lines of 11, to suspect that Baker was displeased that the American mathematicians had not explicitly alluded to his proof; be that as it may, he is at pains to emphasise the reliance of his argument on matrix theory, and adds an explanation of how his proof of 1907 can be shaped so as to dispense with the a posteriori verification of linear independence at the close of Rosati's proof.
This linear independence of two batches of defective integrals came to have, for Baker, another aspect. He encountered, in the study of algebraic correspondences between two curves, precisely two such batches, on one of the curves, whose independence he strongly suspected but was only able to conjecture. The conjecture was, he showed in 13, equivalent to a lemma of Severi (1905) which was well-known both because of its implications in the theory of Picard integrals on a surface and because there was some hesitation, and not only on Baker's part, in accepting Severi's proof as valid. But just before Baker published 13 Hodge, who saw it in manuscript, succeeded in showing that Baker's conjecture was indeed true. There is an incident relating to this conjecture that is not generally known. In the summer of 1929 Baker was lecturing on these topics and put the conjecture to his class. A few days later he asked for our proof, and showed no little chagrin and disappointment that none of us had found one. Had he tried himself? And, if he had, did he guess that he would have to admit failure 7 years later? And, if he did guess so, would he still have felt entitled to, demand success of his class? Perhaps. He had watched T G Room writing his paper on the double-ten with the pride of a chief architect observing the specification of a new cathedral. He was about to communicate J G Semple's paper, on Cremona Transformations in [4], and H S M Coxeter's, on Polytopes with regular-prismatic vertex figures, to successive volumes of the Philosophical Transactions. These essays were hardly such as to cause him to minimise the capabilities of his pupils. Baker rejoiced in their achievements and they gave him ample cause; a Smith's Prize was won by one of them every year from 1927 to 1933, a run of 7 consecutive prizes: few Cambridge teachers can have had so rewarding an experience. Yet these were the years, immediately subsequent to 1926, that saw legions of researchers and a spate of papers on quantum theory. A new pupil, eager to learn geometry, was always warmly welcomed and Baker's satisfaction was deepened when geometry was chosen in conscious preference to the allurements of the new physical discoveries. But he warned newcomers that discoveries in geometry were unlikely to win recognition whereas "if you go and discover a comet you can write a letter to The Times about it." These same years too were the great years of the Baker tea-party: Saturdays at 4.15 during term: a gathering sui generis if ever any gathering was. Any attempt to describe it would be an attempt to communicate the incommunicable. There one listened to the exposition of the embryonic Smith's Prize essays. Most of us were young, but H W Richmond and F S Macaulay aided Baker to leaven the assembly with the senatorial dignity of years.
The momentum of Poincaré's theorem has thrown this biographical notice forward, and one must now revert to the years following 1907. Here it should be said that Baker edited the 4 volumes of Sylvester's papers, totalling more than 2,800 pages; a task spanning the years 1904-12.
In 1910 appeared 4 wherein the theorem of the double-six is proved, without using the cubic surface through the lines, by purely projective arguments that use only lines and quadrics. It is a paper on which its author set some value since, in his candidature for the Lowndean professorship in December 1913, he singles it out, from among the 43 papers he had by then published, as "evidence of the fact that I have cultivated the constructive methods of the old-established geometry." From 1910, too, dates 5, a paper of over 50 pages concerned with the cubic surface. Most of the treatment here is algebraic; Baker pleads that this is "of advantage to readers not familiar with the matter" and adds that a geometrical treatment is much more attractive, an avowal indicative of his growing predilection for geometry. Early in 1912 came 6, exploiting the fact that every algebraic curve on a cubic surface is expressible as a linear combination of 7 curves, namely one twisted cubic and the lines of one half of a double-six. This has, in its final form, an elementary aspect, but it would not have attained this form unless work of Burnside on groups of linear substitutions had recently become available, while the use of a base of 7 curves stems from Severi's work on algebraic surfaces - a topic that made 1912 a significant year for Baker. The International Congress of Mathematicians met at Cambridge; Baker was one of its organising committee of six and presided at the first meeting of the geometry section on 23rd August. The brief address he then gave is a terse summary of the topics which he speaks of in 7, his masterly Presidential Address, read on 12th December, to the London Mathematical Society. This was hailed by a German reviewer as diese anziehend geschriebenen Darstellung der geschichtlichen Entwicklung der neueren Theorie der algebraischen Oberflächen, and so say all of us. It is a splendid document, the ripeness of the subject for exposition combining most felicitously with the erudition and authority of the expositor. Neither the writing nor the reading of it but would he the better for the prelusion of 4 months earlier when the Italian geometers whose work he was extolling were sitting among his audience. At that congress Baker met, for the only time, Castelnuovo, Enriques and Severi.
In 1913 Baker, a widower for 10 years, married again and brought his bride to North Walsham where he owned a house. He now built the house in Storey's Way, then a private road with gates at either end, and during the building travelled to North Walsham for the week-ends in term. Mrs Baker had been brought up in Norfolk, of which both she and her husband were very fond, and they enjoyed long bicycle rides. They named the new house Walcott, after a hamlet near the Norfolk coast east of North Walsham; it is a house that has meant home to them and much to many people, some of whom will call to mind Belloc's apostrophe:
Stand thou for ever among human Houses,But there were no carouses, long or short, at Walcott, and its fame is sure without them. For it is the house where so many pupils were received on so many occasions: where they paid their first tentative call to petition to commence research under the Master: where they received their formidable reading-lists: where they were encouraged in their difficulties and guardedly congratulated on their surmounting them: where they came, established mathematicians, from different continents, to pay their calls. And on the more social visits they were welcomed by a hostess whose staid graciousness will be long remembered.
House of the Resurrection, House of Birth;
House of the rooted hearts and long carouses,
Stand, and be famous over all the Earth.
Baker, while preparing to move into his new home, was appointed to the Lowndean Professorship of Astronomy and Geometry. His claims were very strong, for his publications were voluminous, his erudition profound, and he was now an established teacher of long experience. But some electors might insist on choosing a professor with a knowledge of practical astronomy, and it looks as if they emphatically did. Elections to professorships at Cambridge were presided over by the Vice-Chancellor, who issued the notice of the election on the day the electors met. But Baker's appointment did not conform to this routine - the notice was signed not by the Vice-Chancellor but by the Chancellor, and it was dated not 22nd December 1913, the day that the electors met, but 5th January, 1914. This could be explained by the Vice-Chancellor declining to use a casting vote. Baker's pupils could fittingly make a pilgrimage to Terling Place, Witham, where the Chancellor signed that notice for, in addition to making 5th January 1914 a red-letter day in Baker's life, the appointment has been of immense benefit to the study of geometry at Cambridge and elsewhere. To commemorate our benefactors is a pious duty incumbent on us all, and all who have studied under Baker are eternally indebted to Lord Rayleigh and those who helped to promote Baker to his chair.
These years of the Presidential Address, the second marriage and the appointment to the chair mark a watershed in Baker's life. War supervened, and thereafter Baker was set on the path that he henceforward travelled. His choice of geometry as the dominating intellectual passion of his life is very striking, for he was widely learned and could have been eminent in other branches. He was, after all, of the 19th century and his contemporaries were not prone to specialisation. He lectured on dynamical astronomy almost throughout his tenure of the chair and wrote papers on it as well as on hydrodynamics. In his obituary notice of Poincaré he is every bit as enthusiastic and as well-informed on Poincaré's writings on celestial mechanics as he is on those on automorphic functions and multiply-periodic functions. He proposed the Principle of Least Action for a Smith's Prize essay. Natural Philosophy and its spectacular achievements always captivated him; so close was his long friendship with C T R Wilson that he felt an almost proprietary interest in cloud chambers; he was a friend of P A M Dirac for nigh 30 years and proud that his friendship was reciprocated. But pure mathematics was supreme and, to quote from 8 again, he said publicly
Pure mathematics is not the rival, even less is it the handmaid, of other branches of science. Properly pursued, it is the essence and soul of them all. It is not for them; they are for it; and its results are for all time.
Baker did not leave analysis completely: far from it. The volume G stands to refute any such view. Chapter VII, though perhaps too compressed for so intricate a matter, is concerned with work of Kronecker and Dedekind on the relation between everywhere finite integrals and integral functions. This had been treated-long before in chapter IV of A, and Baker used to say in his old age that something had still to emerge from this arithmetic theory. But he did turn from analysis to geometry. It has been said, and Baker knew of its being said, and by a very eminent mathematician, that Baker thereby made an error of judgment. But Baker, while acknowledging the implied compliment to his early work, did not think so.
Baker was, as all researchers ought to be, always eager to find things out; he wanted to know. Many were the searching interrogatories to which his pupils were subjected. Let one, whereof the occasion is of no importance, serve as an instance. On 26/4/37 he wrote thus.
1. I want to know whether Room has any better method than Dixon's. I cannot find out at present. Grace gives J.L.M.S. 11 an a posteriori verification of the number of constants.
2. I want to know how Dixon's method fits into the usual Abelian thy (my Abelian Fctns. p. 390). It appears to be special for curves of order and equivalent to saying that the general contact curve of order is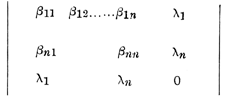
3. I want to know how the contact curve of order on p. 414 of Enriques-Campedelli (Alg. Surf.) fits into the general theory.
4. Now you have found the linear forms for . I should like to know what you get.
I have never properly read Cayley's paper on "Polyzomal curves". I believe you have?
But Baker did not rest content with mere discovery; he wanted an aesthetically satisfying explanation, and the choice between different explanations he would determine by this criterion. This was not a habit only of his later years, it was a lifelong characteristic. In the preface to A he had written:
2. I want to know how Dixon's method fits into the usual Abelian thy (my Abelian Fctns. p. 390). It appears to be special for curves of order and equivalent to saying that the general contact curve of order is
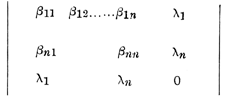
3. I want to know how the contact curve of order on p. 414 of Enriques-Campedelli (Alg. Surf.) fits into the general theory.
4. Now you have found the linear forms for . I should like to know what you get.
I have never properly read Cayley's paper on "Polyzomal curves". I believe you have?
An endeavour has been made to point out what are conceived to be the most artistic ways of formally developing the theory regarded as complete.
He would remark on the long process that began with the struggle of the early 19th century French Dynamiker with the axes of permanent rotation of a rigid body, on how these were then recognised as normals of a set of confocal quadrics, which normals, in their turn, were seen to constitute a tetrahedral complex. Each stage, he would insist, was an advance, but the advance was not complete until Corrado Segre announced that the lines of a tetrahedral complex were just the intersections, of the [3] in which they lay, with those planes that meet 3 given lines in a [4]. Another achievement of Segre's was to geometrise Kronecker's results on a pencil of singular quadratic forms. The difficulty of Kronecker's algebraic reduction is notorious but Segre, by equating a singular form to zero and interpreting the equation as a cone in [], where is the number of variables in the form, considers the locus of vertices (which need not be points merely, but spaces of larger dimension) of the cones. As Baker says in 10 :
To the geometrically minded, to be able to state a geometrical criterion for all the quadrics of the pencil to be singular, of a specified degree, will appeal as a consummation of Kronecker's remarkable work.
A figure might be widely known and have been described by eminent investigators, but yet still be awaiting the best explanation of its raison d'étre. Just after Baker won his Fellowship there was established a birational correspondence between the Weddle surface W and the Kummer surface; it was a consequence of relations between double theta functions. But has it, in essence, anything to do with theta functions? W is the locus of points whereat all quadrics through 6 given points have a common tangent line. Baker, in 3, recalls that the quadrics through 5 points represent the space sections of a Segre cubic primal in [4]; those through 6 points therefore represent the sections through a given point P of the primal. The correspondence is an immediate consequence of the above definition of W and the fact that the apparent contour of the primal from P is a Kummer surface.
The striking elucidations by geometry of phenomena that sprang from other branches of mathematics, the sudden perception in a figure of some intrinsic incandescence, these had a profound effect on and a singular fascination for Baker: as though he were being led to recognise the verities of things sub specie aeternitatis. Herein may well have lain the chief reason for his turning to geometry. He so decided, not in the flush of youthful enthusiasm but in the ripening wisdom of mature years. His high appreciation of analysis remained: Riemann he almost worshipped, so impressed was he with the deep insight of his ideas; the work of Weierstrass and Poincaré he knew as few others could know; yet he chose geometry. Amplissima est et pulcherrima scientia figurarum. So he inscribed the title page of the first volume of Principles of Geometry, and so he believed.
The preceding sentences have indicated that a knowledge of geometry in higher space may be necessary for a proper appreciation of geometry in ordinary space, and Baker's main preoccupation in writing F was to publicise this fact; therein Segre's generation of the tetrahedral complex appears on p. 33 while the Kummer surface is found as an apparent contour on p. 156 and closely scrutinised in chapter VII. Cayley, as long ago as 1846, said, after remarking that Desargues' figure in a plane is a projection of the 10 edges and 10 vertices of a pentahedron, that it was only reasonable to expect, by analogy, a simplification of geometry in space by using figures in higher space. Klein, in 1872, explained how geometries in spaces of different dimensions could be equivalent; a geometry does not depend primarily on the ambient space but on the group of self-transformations of the figure. In Cambridge the situation was fully appreciated by H W Richmond, who had exploited it in papers written about 1900. Yet, at home, there seemed no other awareness and Baker would be pondering again the question of his exordium (7): why is it so often the case that the early history in England of a department of Pure Mathematics is a history of importation? He began to unload his cargo.
In 1920 appeared 9, of which Figure 2 is the well-known frontispiece of F; it supersedes 4 wherein the discussion, repeated at the opening of 9, began with 8 lines in [3] whose relation appears artificial because they are not there recorded as being the projection of a completely natural set of 8 lines in [4]. Though F was not to appear for another 5 years it was already being drafted; meanwhile, as harbingers thereof, C, D, E, were duly issued. Nor was it only Baker who so carefully prepared the ground: the lectures and the advocacy of F P White helped to sow in Cambridge the seed for the approaching harvest. Then the volume came: 1925. For all its idiosyncrasies and, one must declare, its anfractuosities of style it is a glorious book, a cornucopia crammed with riches. The cramming is prodigious. A reviewer wrote:
The book naturally suffers from the compression and is not one to he read in an arm-chair; indeed, any one page will furnish matter for several hours' cogitation by the ordinary mortal. But it is a fascinating study, and British mathematicians may well be proud of such a splendid mine of geometrical lore as is to be found in the four volumes of Principles of Geometry.Not only is every word of this true, but every phrase is an instance of the Englishman's talent for understatement.
A book of such immense influence cannot be adequately summarised here, yet a fair fraction of this notice must be given to it. Perhaps the best course is to give a full account of a certain equivalence, signalised by Klein and exploited by Segre, between geometries in different spaces, and then indicate a few of the many uses to which Baker puts it.
It may help to describe a metrical example before the projective generalisation. Project a sphere stereographically from its north pole onto its equatorial plane . All circles of become circles in , save that circles through become lines. If, then, we regard lines in as special cases of circles, any circle on either or corresponds to a circle on the other. All this is visually obvious when attention is fixed on real points. But points with complex numbers for their co-ordinates are not visible; there are generating lines lying on , two through each point. Such a pair of generators has a real intersection (the only real point on either) and spans a real plane (the tangent plane of at their intersection). The generators and at span the tangent plane at ; this plane is parallel to so that the intersections of with are at "infinity"; moreover they are "conjugate imaginaries." Not only so: both and meet (at conjugate imaginary points) every real plane section of , and indeed and are Poncelet's pair of points common to every circle in . A line in is amplified to a circle by adding the line .
Plane geometry does not demand that the absolute points be either imaginary or at infinity, as they are in the Euclidean plane. So any non-singular quadric can be projected stereographically from any point of onto any plane not through ; the generators of at meet h in points which can serve as absolute points in the plane geometry. Then all plane sections of S are projected into circles while every circle of so arises from a section of S. Chapter II of F opens thus.
Hart's Theorem, for circles in a plane, or for section of a quadric.That is the opening of Chapter II, but the technique has already been applied to much benefit in Chapter I. One must record, writing for an Edinburgh society of which Baker was glad to be an honorary member, his handling of Wallace's theorem (F p. 18). Wallace, who was appointed to the Edinburgh chair in 1819, is usually credited with having been the first to prove, about 1806, that the 4 circles which circumscribe the triangles formed by omitting, in turn, each side of a quadrilateral are concurrent. Baker shows this to be equivalent to a theorem about Möbius tetrahedra - two tetrahedra both inscribed and circumscribed to one another; this theorem in space involves only points, lines and planes. And many additions to and extensions of Wallace's theorem are established.
Given three lines in a plane, there are four circles touching them; these circles, we know, are all touched by another circle, the nine-points circle (Feuerbach's theorem; see Vol. II). In other words, given three lines, we can add to them a circle such that the four, these lines and the circle, are all touched by four other circles.
In the present chapter we show how, given any three circles in a plane, we can add to them another circle, which we call the Hart circle, such that the four circles are all touched by four other circles (Hart, Quart. J. of Maths., IV (1861), p. 260).
The three original circles are in fact touched by eight other circles, as we shall prove. There are fourteen ways of choosing, from these eight, four circles which all touch another circle. In six of these ways, the four circles chosen have a common orthogonal circle; and the four circles consisting of the original circles, and their Hart circle, have also a common orthogonal circle.
We have shown that circles in a plane may be regarded as projections of plane sections of a quadric. We prove the results enunciated as theorems for such plane sections. This appears greatly to increase the interest and clearness of the matter.
It is not possible, by linear transformation in a plane, to turn lines into circles; but it is possible by inversion. In inversive geometry the lines and circles form a closed family. Klein showed, in the Erlanger Programm of 1872, that inversive geometry in a plane is equivalent to projective geometry on a quadric; this is because, the lines and circles in 7) answering to the plane sections of , it is precisely the plane sections of that must form a closed family in a geometry equivalent to the inversive geometry in h so that must, as a surface, be unaltered and its plane sections permuted among themselves. Inversion in a circle of transposes in pairs those points of which do not lie on while leaving every point of invariant: is the projection from of a section of and the inversion answers to a projectivity in space that transposes in pairs those points of that do not lie on while leaving every point of invariant. This is the projectivity that transposes every pair of points on whose join passes through the pole of the plane of . Hence the projection of the curve of intersection of with any cone whose vertex is is its own inverse in . When this cone is a plane the projection is a circle orthogonal to . When it is a quadric cone the situation is fully explained (p. 96) in Chapter III of F, which opens thus.
In this chapter we obtain some properties of a plane curve by projection of a curve which lies in space of three dimensions. The plane curve is one which meets an arbitrary line in four points, and has two double points, or points where the curve crosses itself. The curve in space is the curve of intersection of two quadric surfaces. The matter is dealt with in more detail than is required by its difficulty, because the theory is a model for the subsequent theory of the Cyclide, a quartic surface in three dimensions, regarded as the projection of the intersection of two quadrics of fourfold space. (Chap. VI, below.)For this equivalence between inversion in a plane and geometry on a quadric in space is only an instance, for , of the equivalence between inversion in [] and geometry on a quadric in []. Klein pointed this out and said that it would, for elucidate the properties of cyclides and anallagmatic surfaces. The cyclides had not long to wait for the elucidation. In 1884 Segre published a 130-page paper which is one of the landmarks of descriptive geometry and gives one to understand why Baker spoke, in 10, of Segre's power of fashioning a new world from the bare suggestions of others. After an introduction wherein due acknowledgments are made Segre breaks new ground and, acting on Klein's hint, obtains 78 different types of cyclide as projections of the surface of intersection of two quadrics in [4]. This, with the self-inversions and the generations of a cyclide as an envelope of spheres, is the subject matter of Chapter VI, although Baker, in contrast to Segre's wholly descriptive and synthetic argument, gives a fair amount of algebra. He used to say, years after 1925, that the chapter was too analytical and perhaps, when he wrote it, he was of the same mind, in thinking that algebra would be a help "to readers not familiar with the matter", that he was when he wrote 5. Yet one cannot, whatever his frame of mind, see Baker forgoing the allusions to Maxwell on pp. 193 and 198.
The volumes G and H are quite distinct from C, D, E, F. Baker's intention had been to publish a large volume on the theory of algebraic curves and surfaces which would include a topological treatment of the subject in addition to what has now appeared in G and H; but this third part of the volume was not near enough to completion when Baker began to feel, as a man nearing 70 and tiring, that the compilation of the first two-thirds was perhaps as much as he could confidently hope to accomplish. When he retired from his professorship a dinner was given in his honour in St John's College on Saturday, 6th June 1936. On that day the Edinburgh Mathematical Society was meeting in St Andrews and their congratulatory telegram was put into Baker's hand as he entered college.
In 1941 Baker sent the manuscript of I to the press. He was glad to have done this book and set some store by its logical framework, claiming to start absolutely from scratch with no foundations of Euclid's results or of propositions from "sequels" to Euclid, doing the geometry of circles ab initio. He said modestly when it was finished that he did not think highly of many parts of it, but that it might serve as a model for someone some day to make a less imperfect book. It contains an abundance of examples, and a skilled draughtsman with sufficient leisure could fill a large portfolio with handsome diagrams.
When the war ended Baker was near 80, and the fell sergeant had made his preliminary foray. On 20/7/46 Baker wrote:
Did you ever hear that it was said of - that at a certain stage, smitten by conscience at his unanswered letters, he bought a basket to put them in? I tie mine up with string and they make a pile on the table. Yours has been at the top for a long time.What had laid him abed on 6th May 1944 was pleurisy, and he never walked round the university farm again. The walk had been for years a constant solace: winter and summer, week-days and Sundays, wet or fine, he made the round and his inability to resume it was one of the deep sorrows that tinged his latter days. But, though he might have finished walking, he had not yet finished work. By the middle of September 1945 he had completed the manuscript of J; although he only then assembled it in its final form the subject was clearly in his mind when he wrote 6, and indeed he had been intrigued by it ever since those colloquies with Burkhardt in the distant days at Göttingen. The tract describes the geometry, in [4], of a group of 25920 linear transformations, and its first consequence was J A Todd's using the geometry to decompose the group into its conjugate classes. In the letter, already quoted, of 20/7/46 Baker said:
I have some excuse. I am training for a Valetudinarian, not having ever got back to the vigour I enjoyed before I was laid abed on 6th May 1944. I go short walks, most often in the garden, and, in those terms, am quite well. If you carry out your plan of coming to Cambridge this summer I shall be very glad to see you; but shall not be able to go right round the Farm. I have missed 2 harvests (with this one), to my great regret.
My short screed, in which I use the "synthemes", is in type, with the proofs revised, as a Cambridge-Tract. It will give me much pleasure when I am able to send you a copy. It has inspired Todd, who was kind enough to read the proofs, to write a very remarkable paper on groups - a great satisfaction to me.Todd's paper has proved to be only the first in these last 10 years of at least 10 papers by various authors that would never have been written but for the tract. Moreover it, in its turn, provoked Baker's still insatiable curiosity; by June 1947 he was inquiring how to classify the transformations not as products of projections as Todd, following the tract, did, but by their sets of invariant points. He still wanted to know, and this piece of information he did eventually receive, but only in the closing months of his life when he could no longer see to read it. In 1947 however he was still reading: he read with close attention Hodge and Pedoe's Method of Algebraic Geometry, noting particularly the manner in which they introduced co-ordinates. And at the very end of 1948 he wrote (23/12/48)
I have spent some time of late in looking carefully through (B) Segre's recent "Modern Geometry, Vol. 1", which led me to read van der Waerden's "Algebra, Vol. 1", and the two led me to read about ideals in the old book, Dirichlet's edition of Dedekind's "Theory of Numbers", about a third of which is taken up with the Theory of Ideals.Afterwards he took up the Hodge and Pedoe book again and, in consequence, at the age of 84, wrote 14 and communicated it to the Royal Society on 6th October 1950. This was his last paper, 15 being a brief pendant to it whereby the long procession of impressive works falls quietly to its close with a diagram depicting basic propositions of projective geometry in a plane. The last word lies, after all, with "the constructive methods of the old-established geometry." In minimis maxima.
By the end of 1950 his eyesight was but fitful, and he had to suffer the deprivation of not being able to read on duller days. The cloud of affliction darkened as the last years passed heavily by. In January 1953, he paid the bitter price sometimes exacted for longevity, being predeceased by his younger son. The following December Mrs Baker had to leave home. Pneumonia had hastened the decline of a memory that had begun to fail, and it was essential that she be moved to a nursing home. Baker, though practically confined to his study, was able to make one or two visits by taxi, but it soon became necessary to move her away from Cambridge. The partnership of 40 years was sundered and they never saw one another again. But while these inexorable events could enforce physical separation they could not remove her from his thoughts, and he wrote almost daily. That he felt unable to visit her was a sign of his own awareness of failing strength and, refuse as he might, and for as long as possible, to admit it, his growing realisation that she would not improve (Mrs Baker died on 17th December 1956.) was a potent influence of his own decline. Yet in April 1954, when a colloquium was held in Cambridge, several of his old pupils called to pay their homage and there was no trace in his conversation or demeanour of any resentment or distress. In January 1956 came an onset of phlebitis, while his eyesight by now was poor indeed and, though able to distinguish furniture and large objects, he was quite unable to read. He retained his equanimity throughout and his spirit was still unconquered and undaunted when the end, came peacefully on 17th March.
Baker visited Edinburgh in the first decade of the century, his contemporary F W Dyson being Astronomer Royal for Scotland. An appointment for lunch took him up Blackford Hill, then utterly innocent of suburban contiguity, on a cold winter day in deep snow. The recollection of the stark frigidity of his first climb up that eminence was counterpoised by the warmth of his attachment to it, presided over as it was, from the appointment of Dyson in 1905 till the death of Greaves in 1955, by a personal friend. R A Sampson, who succeeded Dyson in 1910, was 2 years junior to Baker at Cambridge and emulated his friend by winning a Smith's Prize and a St John's Fellowship; this was one of Baker's closest friendships and Sampson was Baker's best man in 1893. But Baker's ties to Scotland were also to other places than Blackford Hill - and other friends than Astronomers Royal. He was an honorary LL.D. of Edinburgh University; he stayed several times with the Whittakers in George Square and had known E T Whittaker and H W Turnbull since their Cambridge days. Turnbull's name is a reminder that Baker's thoughts, when they turned to Scotland, as like as not dwelt longest on the old grey city of St Andrews. He gave courses of lectures there at two colloquia, those of 1926 and 1930. The writer of this notice happened to pay his first call at Walcott in June 1926, and Baker was preparing to leave for St Andrews with Mrs Baker and their daughter in a few days. Twelve years after, on a walk round the Farm, he harked back to this first call and said, with emotion, "Never, never in my life have I enjoyed anything so much as my first visit to St Andrews." At that colloquium H F Baker and H W Richmond used to walk together along the Scores. Those remaining few who beheld that promenade speak about it still, and though the writer did not see it he is able to record it and thereby preserve it from the encroachment of oblivion. Let it be there that we look our last on him, the Cambridge professor savouring the most enjoyable of his too rare holidays, on the meridian of life and at the zenith of happiness, gazing along the West Sands and across the bright estuary to the outline of the Angus hills.
by W L Edge
Baker wrote 10 books, all published by the Cambridge University Press. The dates of the editions are as follows :
A. Abelian Functions 1897
B. Multiply Periodic Functions 1907
Principles of Geometry
C. Foundations 1922, 1929
D. Plane Geometry 1922, 1930
E. Solid Geometry 1923
F. Higher Geometry 1925
G. Theory of Curves 1933
H. Algebraic Surfaces 1933
--------------
I. Introduction to Plane Geometry 1943
J. A locus with 25920 linear self-transformations 1946
The following list of Baker's papers does not include any not referred to in this notice. The list given by Professor Hodge (Biographical Memoirs of Fellows of the Royal Society, Vol. 2) includes 97 papers: a fact that gives some indication of how far, short the above notice falls of an adequate assessment of Baker's work.
1. On the theory of functions of several complex variables.
Trans. Camb. Phil. Soc. 18 (1899), 408.
2. On functions of several variables.
Proc. London Math. Soc.,(2) 1 (1904), 14.
3. Elementary note on the Weddle quartic surface.
Proc. London Math. Soc. (2) 1 (1904), 247.
4. A geometrical proof of the theorem of a double-six of straight lines.
Proc. Royal Soc. (A) 84 (1911), 597.
5. Notes on the theory of the cubic surface.
Proc. London Math. Soc. (2) 9 (1910), 145.
6. On the curves which lie on a cubic surface.
Proc. London Math. Soc. (2) 11 (1912), 285.
7. On some recent advances in the theory of algebraic surfaces.
Proc. London Math. Soc. (2) 12 (1913), 1.
8. The place of pure mathematics.
Nature 92 (1914), 69.
9. On a proof of the theorem of a double-six of lines by projection from four dimensions.
Proc. Camb. Phil. Soc. 20 (1920), 133.
10. Corrado Segre.
Journal London Math. Soc. 1 (1926), 263.
11. On Poincaré's theorem for defective integrals on a Riemann surface.
Journal London Math. Soc. 10 (1935), 281.
12. Note introductory to the study of Klein's group of order 168.
Proc. Camb. Phil. Soc. 31 (1935), 468.
13. On the proof of a lemma enunciated by Severi.
Proc. Camb. Phil. Soc. 32 (1936), 253.
14. On non-commutative algebra, and the foundations of projective geometry.
Proc. Royal Soc. (A) 205 (1951), 178.
15. Note on the foundations of projective geometry.
Proc. Camb. Phil. Soc. 48 (1952), 363.
W L Edge wrote this obituary of H F Baker which was published in the Edinburgh Mathematical Notes. It is a particularly significant obituary since Edge knew Baker well at a personal level and also was a leading expert in geometry.