The development of Galois theory
Fiona Brunk
Galois' predecessors
Joseph-Louis Lagrange (1736-1813) studied the general quintic before was proven that a formula for its solution does not exist. He is widely regarded as the first mathematician who took algebra to a more abstract level. Rather than trying to find some trick which would solve the quintic, Lagrange viewed the solution of the general equation of any particular degree as a special case of a more general problem.
He studied the solutions of the equations of 2nd, 3rd and 4th degree in great detail in order to discover the general pattern. He proved his most important result in Réflexions sur la résolution algébrique des équations, published in 1770/71. It states that in order for an equation to be solvable by radicals, it was necessary that there exists an auxiliary equation. This is an equation whose roots are expressions rational in the roots of the original equation and its coefficients, and whose degree is lower than or equal to the degree of the original equation. Thus solving the auxiliary equation solves the original equation.
Lagrange's aim was still to compute the exact solution of an equation, but he introduced two very important new ways of thinking: firstly, before the roots were actually known, he denoted them by symbols and performed direct computations with them as though they were known. Secondly, he observed that properties of an equation could be deduced from properties of the permutations of its roots. Both of these methods were unheard of at the time and their understanding required a much more abstract way of thinking than the mathematicians of the time were used to.
In particular, Lagrange studied how expressions rational in the roots of an equation changed under permutations of the roots, one of Lagrange's many ideas which Galois was to develop further. For example, since addition in all number systems is commutative and associative, the value of the expression
remains unchanged under all 3! = 6 permutations of x1 , x2 , x3 . On the other hand, the value of the expression
is changed, for instance, by the permutation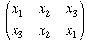
while its value remains constant under the permutation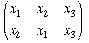
Lagrange showed that in order to find an auxiliary equation of degree lower than that of the original equation of degree n, and thus to solve the general equation of degree n, one had to find an expression rational in the n roots which assumed at most n - 1 values under the n! permutations of the n roots. He found such expressions for n ≤ 4 but could not find one for n = 5. While he may have suspected that this was not possible, he did not succeed in proving it.
Lagrange was interested in the way that expressions in the roots change when permutations are applied to them; he did not study permutations for their own sake. However, he wanted to discover the structure of the solution rather than merely a way to construct the roots. His ideas were revolutionary at the time and of fundamental importance not only to the work of Galois, but to many of his contemporaries such as Abel and Ruffini. Lagrange changed the conception of what it meant to solve an equation, for example by calling an expression "known" once it had been shown to exist. Thus it was no longer necessary to give an explicit construction of the expression, but merely to construct a field in the elements of which the expression was rational. This was one of Lagrange's innovative concepts which helped to prepare the mathematical community for Galois' methods which were even more existential and abstract.
The first mathematician to follow in Lagrange's footsteps was Paolo Ruffini (1765-1822). His work relied heavily on Lagrange's but he went one step further by studying the properties of the permutations themselves, rather than merely their effects on certain expressions. His aim was to prove the unsolvability of the general quintic by radicals, and he published several proofs of this result between 1799 and 1813. However, these proofs rely on a classification of arrangements which the 20th century mathematician Kiernan describes as "extremely awkward" [3], and so it is perhaps not surprising that Ruffini's contemporaries did not accept his proofs. While they accepted some of the intermediate results in the proof, they did not agree that Ruffini's work established the unsolvability of the general equation of fifth degree.
Ruffini, as Lagrange before him, did not employ the purely computational methods of the time when approaching a problem, but instead searched for the underlying, general pattern. The majority of the mathematical community did not understand the arguments of this new generation of mathematicians and followed Legendre's example in dismissing them as "too vague" [1]. However, other important mathematicians such as Cauchy seemed to accept Ruffini's proof. In a letter to Ruffini [1], Cauchy wrote in 1821 that "Your memoir É, in my opinion, proves conclusively the algebraic unsolvability of general equations of higher than fourth degree." Although Cauchy was not prepared to defend Ruffini's work in public, this meant that the mathematical community was progressing further towards an abstract and general understanding of algebra.
Indeed, Augustin-Louis Cauchy (1789-1857) was the first mathematician who studied the properties of permutations extensively for their own sake. He defined many important terms, e.g. a permutation and its order, a cyclic permutation and its powers, a transposition, etc. He also defined the multiplication of two permutations and introduced the notation for permutations which we still use today. In his papers, Galois quoted results by mathematicians of the time such as Cauchy and Carl Friedrich Gauss (1777-1855) who, as an application of some of his number theoretic results, proved the solvability by radicals of for any positive integer n.
After Ruffini's death, the work of Niels Henrik Abel (1802-1829) kept the interest in the solvability of equations alive. Between 1824 and 1828, Abel published several proofs of the unsolvability of the general equation of degree five. While we know today that Abel's proof was not entirely rigorous (since [3] he uses the kth roots of unity (where k is less than the degree of the general equation being solved) without ever making the required assumption that these are in the field of coefficients, or adjoined to it) it represents an important step in the development of Galois Theory because Abel's contemporaries accepted his proof as sufficient.
Even at the time, Abel's proof was criticised as lengthy and computational. His main concern was the explicit construction of the roots of a given equation and his proofs were almost entirely based on extensive direct computations. So unlike Ruffini, Abel was not part of the new generation of mathematicians who were searching for the underlying general structure of a problem and approaching mathematics in a more abstract way. However, Abel finally settled the question of the solvability of the general quintic which meant that the mathematicians who followed were now free to concentrate their efforts on the solvability of special equations.
He studied the solutions of the equations of 2nd, 3rd and 4th degree in great detail in order to discover the general pattern. He proved his most important result in Réflexions sur la résolution algébrique des équations, published in 1770/71. It states that in order for an equation to be solvable by radicals, it was necessary that there exists an auxiliary equation. This is an equation whose roots are expressions rational in the roots of the original equation and its coefficients, and whose degree is lower than or equal to the degree of the original equation. Thus solving the auxiliary equation solves the original equation.
Lagrange's aim was still to compute the exact solution of an equation, but he introduced two very important new ways of thinking: firstly, before the roots were actually known, he denoted them by symbols and performed direct computations with them as though they were known. Secondly, he observed that properties of an equation could be deduced from properties of the permutations of its roots. Both of these methods were unheard of at the time and their understanding required a much more abstract way of thinking than the mathematicians of the time were used to.
In particular, Lagrange studied how expressions rational in the roots of an equation changed under permutations of the roots, one of Lagrange's many ideas which Galois was to develop further. For example, since addition in all number systems is commutative and associative, the value of the expression
remains unchanged under all 3! = 6 permutations of x1 , x2 , x3 . On the other hand, the value of the expression
is changed, for instance, by the permutation
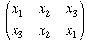
while its value remains constant under the permutation
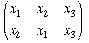
Lagrange showed that in order to find an auxiliary equation of degree lower than that of the original equation of degree n, and thus to solve the general equation of degree n, one had to find an expression rational in the n roots which assumed at most n - 1 values under the n! permutations of the n roots. He found such expressions for n ≤ 4 but could not find one for n = 5. While he may have suspected that this was not possible, he did not succeed in proving it.
Lagrange was interested in the way that expressions in the roots change when permutations are applied to them; he did not study permutations for their own sake. However, he wanted to discover the structure of the solution rather than merely a way to construct the roots. His ideas were revolutionary at the time and of fundamental importance not only to the work of Galois, but to many of his contemporaries such as Abel and Ruffini. Lagrange changed the conception of what it meant to solve an equation, for example by calling an expression "known" once it had been shown to exist. Thus it was no longer necessary to give an explicit construction of the expression, but merely to construct a field in the elements of which the expression was rational. This was one of Lagrange's innovative concepts which helped to prepare the mathematical community for Galois' methods which were even more existential and abstract.
The first mathematician to follow in Lagrange's footsteps was Paolo Ruffini (1765-1822). His work relied heavily on Lagrange's but he went one step further by studying the properties of the permutations themselves, rather than merely their effects on certain expressions. His aim was to prove the unsolvability of the general quintic by radicals, and he published several proofs of this result between 1799 and 1813. However, these proofs rely on a classification of arrangements which the 20th century mathematician Kiernan describes as "extremely awkward" [3], and so it is perhaps not surprising that Ruffini's contemporaries did not accept his proofs. While they accepted some of the intermediate results in the proof, they did not agree that Ruffini's work established the unsolvability of the general equation of fifth degree.
Ruffini, as Lagrange before him, did not employ the purely computational methods of the time when approaching a problem, but instead searched for the underlying, general pattern. The majority of the mathematical community did not understand the arguments of this new generation of mathematicians and followed Legendre's example in dismissing them as "too vague" [1]. However, other important mathematicians such as Cauchy seemed to accept Ruffini's proof. In a letter to Ruffini [1], Cauchy wrote in 1821 that "Your memoir É, in my opinion, proves conclusively the algebraic unsolvability of general equations of higher than fourth degree." Although Cauchy was not prepared to defend Ruffini's work in public, this meant that the mathematical community was progressing further towards an abstract and general understanding of algebra.
Indeed, Augustin-Louis Cauchy (1789-1857) was the first mathematician who studied the properties of permutations extensively for their own sake. He defined many important terms, e.g. a permutation and its order, a cyclic permutation and its powers, a transposition, etc. He also defined the multiplication of two permutations and introduced the notation for permutations which we still use today. In his papers, Galois quoted results by mathematicians of the time such as Cauchy and Carl Friedrich Gauss (1777-1855) who, as an application of some of his number theoretic results, proved the solvability by radicals of for any positive integer n.
After Ruffini's death, the work of Niels Henrik Abel (1802-1829) kept the interest in the solvability of equations alive. Between 1824 and 1828, Abel published several proofs of the unsolvability of the general equation of degree five. While we know today that Abel's proof was not entirely rigorous (since [3] he uses the kth roots of unity (where k is less than the degree of the general equation being solved) without ever making the required assumption that these are in the field of coefficients, or adjoined to it) it represents an important step in the development of Galois Theory because Abel's contemporaries accepted his proof as sufficient.
Even at the time, Abel's proof was criticised as lengthy and computational. His main concern was the explicit construction of the roots of a given equation and his proofs were almost entirely based on extensive direct computations. So unlike Ruffini, Abel was not part of the new generation of mathematicians who were searching for the underlying general structure of a problem and approaching mathematics in a more abstract way. However, Abel finally settled the question of the solvability of the general quintic which meant that the mathematicians who followed were now free to concentrate their efforts on the solvability of special equations.