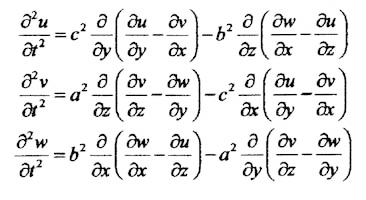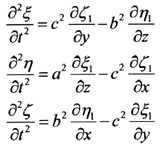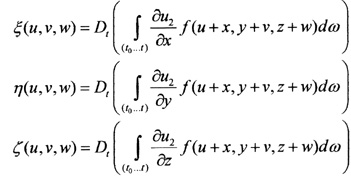Sofia Kovalevskaya
Leigh Ellison
The Lamé Equations
In his work on a systematic dynamical theory of elasticity Gabriel Lamé derived from Newtonian mechanics his basic equations which are also the conditions for equilibrium. From those he went on to derive what are now known as the Lamé equations:
On suggesting that Sofia investigate the refraction of light in a crystalline medium, Weierstrass have her one of his many unpublished papers which included a very clever method of constructing what we now call Green's function for certain initial-value problems. Thus the only version which we have today of this work by Weierstrass is the one published by Sofia in the first half of this paper.
In the second half of the paper Sofia assumed certain solutions to the above equations in order to reduce them to
She then used a combination of differentiation, integration and substitution on the way to solving the equations.
Sofia's final formulation for the solution to the equations was
Unfortunately this supposed solution is not one at all. If you look at the case f(x, y z) = y for example, the result is then ξ = 0, η = 0, ζ = Ct2 where C is a positive constant. These functions therefore do not satisfy Lamé's equations. Sofia, Weierstrass and Runge all failed to notice this which merely shows how uninterested each of them was in the result. Sofia's personal life was unstable while she worked on this particular problem, Weierstrass was going through one of his periods of poor health, while Runge cannot be blamed for his lack of interest while proof-reading the work of a friend.
Sofia had argued that her solution must be correct because the method used to arrive at it deemed that it must be. This was a common procedure during this particular period, but still doesn't really explain why a better check was not carried out. The error did not come to light until Vito Volterra discovered it several months after Sofia's death. This fact alone shows how relatively unimportant this paper was. In bringing to light a previously unpublished paper by Weierstrass and allowing Sofia to immerse herself once more in the world of mathematics, it nevertheless was of value. She certainly managed to improve on the previous work of Lamé in this area.
On suggesting that Sofia investigate the refraction of light in a crystalline medium, Weierstrass have her one of his many unpublished papers which included a very clever method of constructing what we now call Green's function for certain initial-value problems. Thus the only version which we have today of this work by Weierstrass is the one published by Sofia in the first half of this paper.
In the second half of the paper Sofia assumed certain solutions to the above equations in order to reduce them to
She then used a combination of differentiation, integration and substitution on the way to solving the equations.
Sofia's final formulation for the solution to the equations was
Unfortunately this supposed solution is not one at all. If you look at the case f(x, y z) = y for example, the result is then ξ = 0, η = 0, ζ = Ct2 where C is a positive constant. These functions therefore do not satisfy Lamé's equations. Sofia, Weierstrass and Runge all failed to notice this which merely shows how uninterested each of them was in the result. Sofia's personal life was unstable while she worked on this particular problem, Weierstrass was going through one of his periods of poor health, while Runge cannot be blamed for his lack of interest while proof-reading the work of a friend.
Sofia had argued that her solution must be correct because the method used to arrive at it deemed that it must be. This was a common procedure during this particular period, but still doesn't really explain why a better check was not carried out. The error did not come to light until Vito Volterra discovered it several months after Sofia's death. This fact alone shows how relatively unimportant this paper was. In bringing to light a previously unpublished paper by Weierstrass and allowing Sofia to immerse herself once more in the world of mathematics, it nevertheless was of value. She certainly managed to improve on the previous work of Lamé in this area.