Indian Mathematics - Redressing the balance
Ian G Pearce
Decimal numeration and the place-value system
I have already mentioned on several occasions the development of a decimal place value system of numeration and there is now very little doubt among historians that this invention originated from the Indian subcontinent. That said, it was considered, until recently, that Arabic scholars were responsible for the system, as C Srinivasiengar writes:
Further attempts have been made to attribute the first use of a place value system to the ancient Babylonian civilisation of Mesopotamia. While it cannot be denied that the Babylonians used a place value system, their's was sexagismal (base 60), and while the concept of place value may have come from Mesopotamia, the Indians were the first to use it with a decimal base (base 10).
All current evidence points towards the Indian system having been influenced by the base 10 Chinese 'counting boards' and the place value system of the Babylonians but combined use of decimal numerals and place value first occurred on the Indian subcontinent. Without doubt the use of a decimal base originates from the most basic human instinct of counting on one's fingers. The key contribution of the Indians however is not in the development of nine (recognisable) symbols to represent the numbers one to nine, but the invention of the place holder zero.
The great 18th century European mathematician Laplace best described the 'invention' of the decimal place value system as such:
Beyond not being fully appreciated D Duncan discusses briefly the enduring problem of Eurocentric scholars who long assumed the symbol for zero was a Greek invention, with no proof at all. The claims were based of pure speculations that zero came from the Greek letter omicron (O), the first letter of the Greek word ouden meaning empty. We know this to be untrue, but it serves as a timely reminder of the struggle for recognition of Indian mathematical developments.
There is wide ranging debate as to when the decimal place value system was developed, but there is significant evidence that an early system was in use by the inhabitants of the Indus valley by 3000 BC. Excavations at both Harappa and Mohenjo Daro have supported this theory. At this time however a 'complete' place value system had not yet been developed and along with symbols for the numbers one through nine, there were also symbols for 10, 20, 100 and so on.
The formation of the numeral forms as we know them now has taken several thousand years, and for quite some time in India there were several different forms. These included Kharosthi and Brahmi numerals, the latter were refined into the Gwalior numerals, which are notably similar to those in use today (see Figure 7.1). Study of the Brahmi numerals has also lent weight to claims that decimal numeration was in use by the Indus civilisation as correlations have been noted between the Indus and Brahmi scripts.
It is uncertain how much longer it took for zero to be invented but there is little doubt that such a symbol was in existence by 500 BC, if not in widespread use. Evidence can be found in the work of the famous Indian grammarian Panini (5th or 6th century BC) and later the work of Pingala a scholar who wrote a work, Chhandas-Sutra (c. 200 BC). The first documented evidence of the use of zero for mathematical purposes is not until around 2nd century AD (in the Bakhshali manuscript). The first recorded 'non-mathematical' use of zero dates even later, around 680 AD, the number 605 was found on a Khmer inscription in Cambodia. Despite this it seems certain that a symbol was in use prior to that time. B Datta and A Singh discuss the likelihood that the decimal place value system, including zero had been 'perfected' by 100 BC or earlier. Although there is no concrete evidence to support their claims, they are established on the very solid basis that new number systems take 800 to 1000 years to become 'commonly' used, which the Indian system had done by the 9th century AD.
The inventor of the zero symbol is unknown, but what is known is that it was firstly denoted by a dot, then possibly a circle with a dot in the centre, and later by the oval shape we now use. Prior to its invention, Indian mathematicians had already taken to leaving an empty column on their counting boards and clearly at some point this empty space was filled. The Indians referred to zero as 'sunya' meaning void. Again, although evidence points towards a Mesopotamian origin for a place holder, their 'zero' (two slanted bars) was not used in conjunction with a decimal base.
Having become firmly established in academic circles in India by the 6th century, the decimal place value system spread across the world. Initially to China and Alexandria, then to the Arab empire where it became the system of choice of the scholars in Baghdad by the 8th century.
Arabic scholars during this time improved the system by introducing decimal fractions. The system also spread into Spain, as has been previously discussed southern Spain was under Arabic rule into the 12th century. It took much longer for the system to be accepted in mainland Europe, but eventually by the 16th century it was widely used. That said, both prejudice and suspicion continued to be widespread, while orthodoxy also played its part in the continued use of Roman numerals. The last significant case of an attempt to abolish the Indian decimal place value system was in Sweden in the early 18th century.
This is clearly a very brief overview of the phenomenal development of the decimal place value system, without which it is accepted 'higher mathematics' would not be possible. It is impossible for me to do justice to its importance in such few words, so I will conclude with a quote from G Halstead who commented:
Figure 7.1: Indian numeral forms. [GJ, P 241]

Figure 7.2: Numeral forms found in Bakhshali Manuscript, showing place value and use of zero. [GJ, P 241]
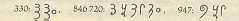
Figure 7.3: Brahmi numerals. [DD, P 163]
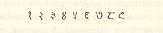
Figure 7.4: Progression of Brahmi number forms through the centuries (column far left showing forms in use by 500 AD). [AS/BD (vol. 1), P 120]

Figure 7.5: Numerical forms (including zero) by found in 20th century Indian texts. [AS/BD (vol. 1), P 121]

...During the earlier decades of this century (20th) attempts were made to credit this invention wholly or in part to the Arabs. [CS, P 2]
Further attempts have been made to attribute the first use of a place value system to the ancient Babylonian civilisation of Mesopotamia. While it cannot be denied that the Babylonians used a place value system, their's was sexagismal (base 60), and while the concept of place value may have come from Mesopotamia, the Indians were the first to use it with a decimal base (base 10).
All current evidence points towards the Indian system having been influenced by the base 10 Chinese 'counting boards' and the place value system of the Babylonians but combined use of decimal numerals and place value first occurred on the Indian subcontinent. Without doubt the use of a decimal base originates from the most basic human instinct of counting on one's fingers. The key contribution of the Indians however is not in the development of nine (recognisable) symbols to represent the numbers one to nine, but the invention of the place holder zero.
The great 18th century European mathematician Laplace best described the 'invention' of the decimal place value system as such:
...The idea of expressing all quantities by nine figures whereby is imparted to them both an absolute value and one by position is so simple that this very simplicity is the very reason for our not being sufficiently aware how much admiration it deserves. [CS, P 5]
Beyond not being fully appreciated D Duncan discusses briefly the enduring problem of Eurocentric scholars who long assumed the symbol for zero was a Greek invention, with no proof at all. The claims were based of pure speculations that zero came from the Greek letter omicron (O), the first letter of the Greek word ouden meaning empty. We know this to be untrue, but it serves as a timely reminder of the struggle for recognition of Indian mathematical developments.
There is wide ranging debate as to when the decimal place value system was developed, but there is significant evidence that an early system was in use by the inhabitants of the Indus valley by 3000 BC. Excavations at both Harappa and Mohenjo Daro have supported this theory. At this time however a 'complete' place value system had not yet been developed and along with symbols for the numbers one through nine, there were also symbols for 10, 20, 100 and so on.
The formation of the numeral forms as we know them now has taken several thousand years, and for quite some time in India there were several different forms. These included Kharosthi and Brahmi numerals, the latter were refined into the Gwalior numerals, which are notably similar to those in use today (see Figure 7.1). Study of the Brahmi numerals has also lent weight to claims that decimal numeration was in use by the Indus civilisation as correlations have been noted between the Indus and Brahmi scripts.
It is uncertain how much longer it took for zero to be invented but there is little doubt that such a symbol was in existence by 500 BC, if not in widespread use. Evidence can be found in the work of the famous Indian grammarian Panini (5th or 6th century BC) and later the work of Pingala a scholar who wrote a work, Chhandas-Sutra (c. 200 BC). The first documented evidence of the use of zero for mathematical purposes is not until around 2nd century AD (in the Bakhshali manuscript). The first recorded 'non-mathematical' use of zero dates even later, around 680 AD, the number 605 was found on a Khmer inscription in Cambodia. Despite this it seems certain that a symbol was in use prior to that time. B Datta and A Singh discuss the likelihood that the decimal place value system, including zero had been 'perfected' by 100 BC or earlier. Although there is no concrete evidence to support their claims, they are established on the very solid basis that new number systems take 800 to 1000 years to become 'commonly' used, which the Indian system had done by the 9th century AD.
The inventor of the zero symbol is unknown, but what is known is that it was firstly denoted by a dot, then possibly a circle with a dot in the centre, and later by the oval shape we now use. Prior to its invention, Indian mathematicians had already taken to leaving an empty column on their counting boards and clearly at some point this empty space was filled. The Indians referred to zero as 'sunya' meaning void. Again, although evidence points towards a Mesopotamian origin for a place holder, their 'zero' (two slanted bars) was not used in conjunction with a decimal base.
Having become firmly established in academic circles in India by the 6th century, the decimal place value system spread across the world. Initially to China and Alexandria, then to the Arab empire where it became the system of choice of the scholars in Baghdad by the 8th century.
Arabic scholars during this time improved the system by introducing decimal fractions. The system also spread into Spain, as has been previously discussed southern Spain was under Arabic rule into the 12th century. It took much longer for the system to be accepted in mainland Europe, but eventually by the 16th century it was widely used. That said, both prejudice and suspicion continued to be widespread, while orthodoxy also played its part in the continued use of Roman numerals. The last significant case of an attempt to abolish the Indian decimal place value system was in Sweden in the early 18th century.
This is clearly a very brief overview of the phenomenal development of the decimal place value system, without which it is accepted 'higher mathematics' would not be possible. It is impossible for me to do justice to its importance in such few words, so I will conclude with a quote from G Halstead who commented:
...The importance of the creation of the zero mark can never be exaggerated. This giving to airy nothing, not merely a local habituation and a name, a picture, a symbol but helpful power, is the characteristic of the Hindu race from whence it sprang. No single mathematical creation has been more potent for the general on go of intelligence and power. [CS, P 5]
Figure 7.1: Indian numeral forms. [GJ, P 241]

Figure 7.2: Numeral forms found in Bakhshali Manuscript, showing place value and use of zero. [GJ, P 241]
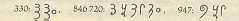
Figure 7.3: Brahmi numerals. [DD, P 163]
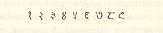
Figure 7.4: Progression of Brahmi number forms through the centuries (column far left showing forms in use by 500 AD). [AS/BD (vol. 1), P 120]

Figure 7.5: Numerical forms (including zero) by found in 20th century Indian texts. [AS/BD (vol. 1), P 121]
