William Wallace's proof of the "butterfly theorem"
Problem
is the diameter of a Circle, a chord cutting it at right angles in and two other chords drawn anyhow through the point , and chords joining the extremes of . It is required to prove that is equal to .
Demonstration
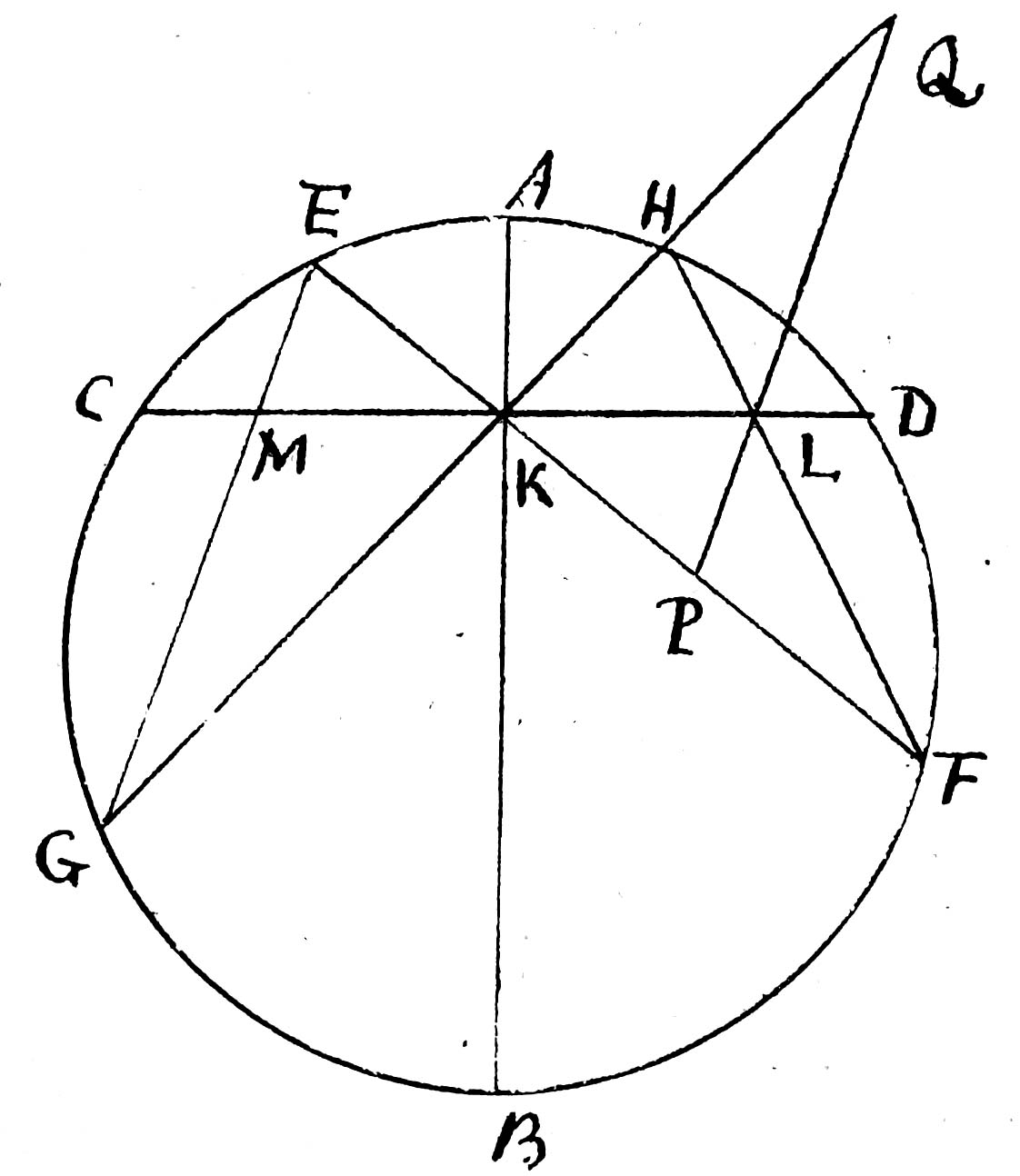
Through draw parallel to , meeting in and in .
Because of the parallels the angle is equal to , but is equal to , or to , for they are in the same segment, therefore the angles are equal, and hence the points are in the circumference of a circle, wherefore .
The triangles are similar and their sides are similarly divided by the lines , which lines are to each other as to , and as to , therefore
, or ;
that is
and by composition, &c.
But &
Therefore , and .
But being perpendicular to the diameter, is equal to ,
therefore must also be equal to as was to be demonstrated.
Remark
The above proposition is a particular case of a more general one extending to all the Conic Sections, which may be expressed thus.
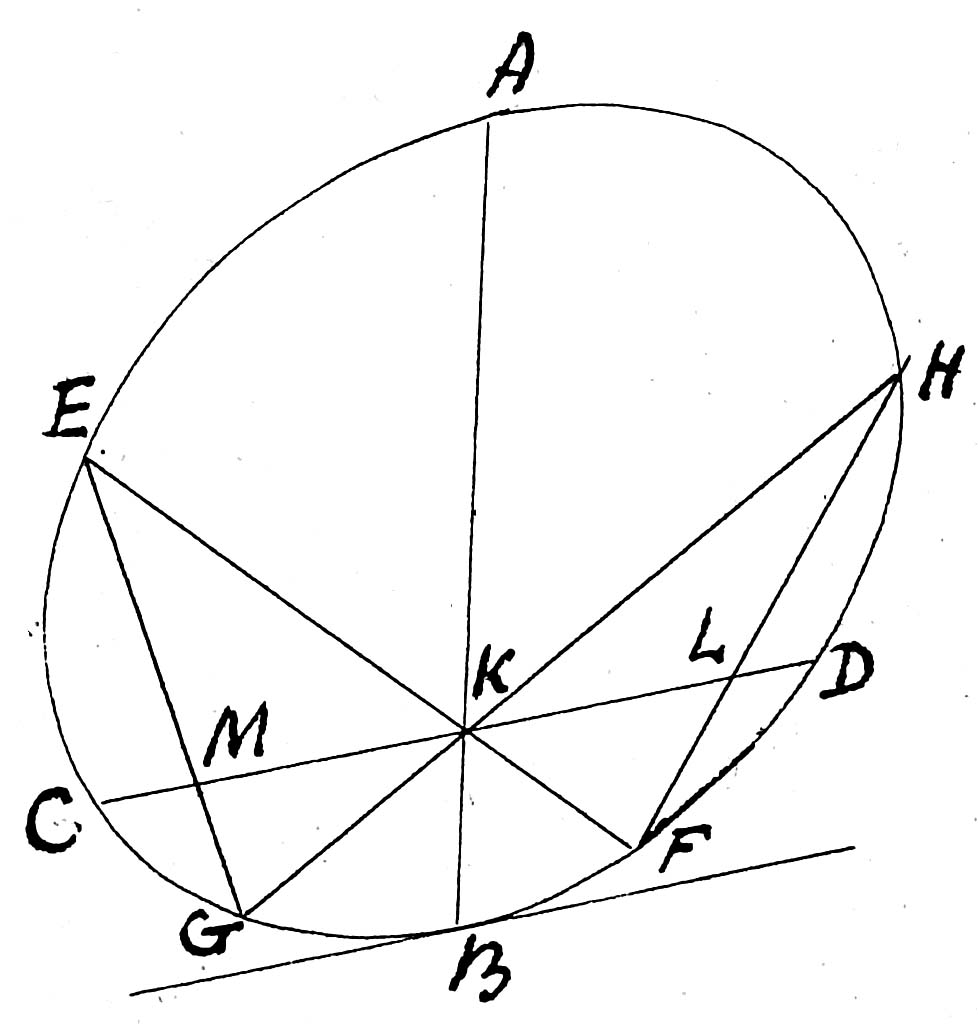
If is any diameter of a Conic Section, and any right line cutting it in , and parallel to a tangent at its vertices; also and two other lines drawn anyhow through , to meet the conic section, the one in the points , and the other in the points , the straight lines which join the extremities of these lines shall intercept upon the segments which are equal to each other.
W. Wallace
is the diameter of a Circle, a chord cutting it at right angles in and two other chords drawn anyhow through the point , and chords joining the extremes of . It is required to prove that is equal to .
Demonstration

Through draw parallel to , meeting in and in .
Because of the parallels the angle is equal to , but is equal to , or to , for they are in the same segment, therefore the angles are equal, and hence the points are in the circumference of a circle, wherefore .
The triangles are similar and their sides are similarly divided by the lines , which lines are to each other as to , and as to , therefore
, or ;
that is
and by composition, &c.
But &
Therefore , and .
But being perpendicular to the diameter, is equal to ,
therefore must also be equal to as was to be demonstrated.

Remark
The above proposition is a particular case of a more general one extending to all the Conic Sections, which may be expressed thus.
If is any diameter of a Conic Section, and any right line cutting it in , and parallel to a tangent at its vertices; also and two other lines drawn anyhow through , to meet the conic section, the one in the points , and the other in the points , the straight lines which join the extremities of these lines shall intercept upon the segments which are equal to each other.
W. Wallace