Pierre René Jean Baptiste Henri Brocard
Quick Info
Vignot (part of Commercy), France
Bar-le-Duc, France
Biography
Henri Brocard's parents were Elizabeth Auguste Liouville and Jean Sebastien Brocard. He attended the Lycée in Marseilles, moving from there to the Lycée in Strasbourg. After graduating from the Lycée he entered the Academy in Strasbourg where he was coached to take the entrance examinations of the École Polytechnique in Paris.Brocard studied at the École Polytechnique from 1865 to 1867. Most graduates at this time became technical officers in the military forces and indeed that is exactly the route which Brocard took, joining the Engineering Corps in the French Army. He was joining an army which had been reorganised shortly before (in 1866) and all France was confident of its abilities. Brocard taught for a short while in Montpellier. Most of his army career was spent in teaching and research, with his first mathematical articles published in 1868, but he did see active service quite soon in his career.
The popularity of Napoleon III, the French emperor, was declining in France and he thought a war with Prussia might change his political fortunes since his advisers told him that the newly reorganised French Army could defeat Prussia. Bismarck, the Prussian chancellor, saw a war with France as an opportunity to unite the South German states. With both sides feeling that a war was to their advantage, the Franco-Prussian War became inevitable. On 14 July 1870, Bismarck sent a telegram aimed at infuriating the French government. He succeeded, for on the 19 July France declared war on Prussia very confident that their newly reorganised army was superior to that of the Prussians. Brocard was with the 120,000 French troops under Marshal MacMahon accompanied by Napoleon III. They moved towards Metz where the French Army of the Rhine was trapped. However, Prussian intelligence worked out their movements and engaged them on 29 and 31 August on the river Meuse. The French fell back to the fortress at Sedan where they were encircled by the Prussian troops. After attempting to break out on a number of occasions, the French suffered heavy losses. When the Prussians attacked them on 1 September the French surrendered. Brocard was one of 83,000 French soldiers taken as prisoners of war at Sedan.
The war was an embarrassing defeat for the French. After Brocard was released he returned to his army life of teaching and research. The French Mathematical Society, Société Mathématique de France, was founded in 1872 and Brocard joined the Society in the year after it was founded. In 1875 he was made a life member of the French Association for the Advancement of Science and the French Meteorological Society. By this time, however, he was in north Africa where he had been sent. He spent around ten years, from 1874 to 1884, in north Africa. Mostly he was in Algiers which, after being captured by the French in 1830, had been made the military and administrative headquarters for their African empire. At the Congress of Berlin in 1878 the British withdrew their objections to French expansion in North Africa. Tunisia then became a French protectorate in 1881-83. Brocard took part in the scientific life of Algiers, being a cofounder of the Meteorological Institute there, and a member of the local committee of the meeting of the French Association for the Advancement of Science in Algiers in 1881. At this meeting Brocard delivered a paper Études d'un nouveau cercle du plan du triangle Ⓣ which contains what is known today as the 'Brocard circle' (see below). During his ten years in North Africa, Brocard also spent time in Oran, which was occupied by the French in 1831 and turned by them into a modern port and major naval base.
In 1884 Brocard returned to France where he served with the Meteorological Commission in Montpellier, Genoble and Bar-le-duc. He continued to serve with the army until he retired in 1910 having reached the rank of lieutenant colonel. He served on many government commissions and was an active mathematician, as he had been throughout his life. He published in many different journals, but his two major publications were the two volumes of Notes de bibliographie des corbes géométriques Ⓣ (1897, 1899) and the two volumes of Courbes géométriques remarkables the first of which was published in 1920, the second in 1967 long after his death. This last work was written in collaboration with T Lemoyne [1]:-
The Notes may be regarded as a source book of geometric curves, with a painstakingly prepared index containing more than a thousand named curves. The text consists of brief descriptive paragraphs, with diagrams and equations of these curves.
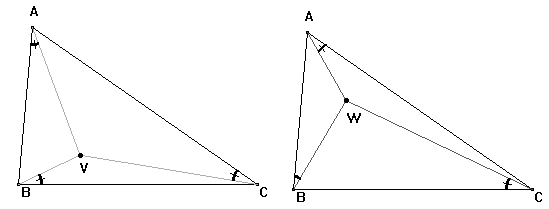
[Draw a circle tangent to at passing through , another tangent to at passing through , a third tangent to at passing through . They are concurrent at ]
Angle is called the Brocard angle and satisfies
.
The Brocard circle is that drawn on a diameter, the end points of which are the circumcentre and symmedian point of the triangle. It passes through the Brocard points.
Although best known through this work on the triangle, Brocard also made other contributions which have proved important. The problem of Brocard referred to in [2] is the following. In 1876, Brocard asked if the only solutions to the equation , in positive integers , are (4, 5), (5, 11), (7, 71). This problem remains open. It is not even known whether there are only finitely many solutions. Let us mention a further contribution, this time to pursuit curves. A pursuit curve is that traced out by a point if it is always directed towards a point tracing out some curve, both points moving with the same velocity. The idea was introduced by Bouguer around 1732. In 1877 Lucas asked what curves would be traced out by three dogs, initially at the vertices of an equilateral triangle, if they run one after the other. In 1880 Brocard showed that each dog's pursuit curve would be that of a logarithmic spiral and that the dogs would meet at a common point. This point is now known as the Brocard point of the triangle.
Brocard spent the last years of his life in Bar-le-Duc as a somewhat solitary figure. He was an only child, and had no close family. He never married and seldom entertained friends. He did, however, continue to take an active part in scientific life, being the librarian of the Bar-le-Duc Society of Letters, Sciences, and Arts. He declined the offer to become president of the Society. He spent many hours making astronomical observations from his back garden. He attended the International Congress of Mathematicians at Zürich in 1897, Paris in 1900, Heidelberg in 1904, Rome in 1908, Cambridge, England in 1912, and Strasbourg in 1920.
Guggenbuhl writes in [1]:-
On 16 January 1922, Brocard was found dead at his desk. In accordance with his specific request, he was buried in the small cemetery at Vignot, next to his father and mother.
References (show)
- L Guggenbuhl, Biography in Dictionary of Scientific Biography (New York 1970-1990). See THIS LINK.
- A Gica and L Panaitopol, On a problem of Brocard, Bull. London Math. Soc. 37 (4) (2005), 502-506.
- L Guggenbuhl, Henri Brocard and the Geometry of the triangle, Mathematical Gazette 32 (1953), 241-243.
- R J Stroeker, Brocard points, circulant matrices, and Descartes' folium, Math. Mag. 61 (3) (1988), 172-187.
Additional Resources (show)
Other pages about Henri Brocard:
Other websites about Henri Brocard:
Cross-references (show)
Written by J J O'Connor and E F Robertson
Last Update August 2006
Last Update August 2006
