Dinostratus
Quick Info
Greece
Biography
Dinostratus is mentioned by Proclus who says (see for example [1] or [3]):-Amyclas of Heraclea, one of the associates of Plato, and Menaechmus, a pupil of Eudoxus who had studied with Plato, and his brother Dinostratus made the whole of geometry still more perfect.It is usually claimed that Dinostratus used the quadratrix, discovered by Hippias, to solve the problem of squaring the circle. Pappus tells us (see for example [1] or [3]):-
For the squaring of the circle there was used by Dinostratus, Nicomedes and certain other later persons a certain curve which took its name from this property, for it is called by them square-forming [in other words the quadratrix].It appears from this quote that Hippias discovered the curve but that it was Dinostratus who was the first to use it to find a square equal in area to a given circle. Proclus, who claims to be quoting from Eudemus, writes (see [1]):-
Nicomedes trisected any rectilinear angle by means of the conchoidal curves, of which he had handed down the origin, order, and properties, being himself the discoverer of their special characteristic. Others have done the same thing by means of the quadratrices of Hippias and Nicomedes.This makes somewhat less convincing the claim that Dinostratus used the quadratrix, discovered by Hippias, to square the circle since Eudemus does not even mention Dinostratus. There is also a suggestion that Hippias wrote a treatise on the quadratrix and if this is the case it seems hard to believe that he did not show how it could be used to square the circle.
Whether Dinostratus was indeed the first to square the circle using the quadratrix seems almost irrelevant for, as Bulmer-Thomas writes in [1]:-
... posterity has firmly associated the name of Dinostratus with the quadrature of the circle by means of the quadratrix.
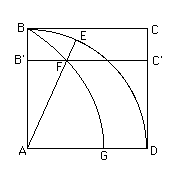
Pappus relates how the quadratrix was used to square the circle. The construction of the curve is described in the article on Hippias. The quadratrix meets the line in the point and
so the length of the circumference of the circle is expressed in terms of the lengths of straight lines. This leads to the construction of a square equal to the circle.
Pappus reports that Sporus was critical of this construction. He had two objections, the first of which relates to the construction of the quadratrix itself (see the article on Hippias). The second objection relates to Dinostratus's use of the quadratrix to square the circle. Sporus claims that the moving line never cuts the line and so the point is not determined. The point can only be found as a limit. There is no doubt that Sporus is quite correct with his objection.
Dinostratus probably did much more work on geometry but nothing is known of it.
References (show)
- I Bulmer-Thomas, Biography in Dictionary of Scientific Biography (New York 1970-1990).
See THIS LINK. - G J Allman, Greek geometry from Thales to Euclid (Dublin, 1889).
- T L Heath, A History of Greek Mathematics I (Oxford, 1921).
- B L van der Waerden, Science awakening (Groningen, 1954).
Additional Resources (show)
Other pages about Dinostratus:
Other websites about Dinostratus:
Cross-references (show)
Written by J J O'Connor and E F Robertson
Last Update April 1999
Last Update April 1999