Cecil John Alvin Evelyn
Quick Info
London, England
Deptford, Kent, England
Biography
John Evelyn was the son of John Harcourt Chichester Evelyn (1876-1922), the son of William John Evelyn and Frances Harriet Chichester, and Frances Edith Ives (1878-1935), the daughter of Major-General Cecil Robert St John Ives and the Honourable Susan Ann Talbot. John Harcourt Chichester Evelyn was a pupil at the leading independent school Eton College before studying at Christ Church, University of Oxford. He became a military man who served in the Boer War and World War I. He was wounded in World War I and, although he lived for a few more years, he died from his wounds in January 1922. He had married Frances Edith Ives on 27 January 1902 and they had three children, Susanna Frances Evelyn, Cecil John Alvin Evelyn (the subject of this biography), and Peter George Evelyn (1909-1945). Peter George Evelyn, like his father, became a military man rising to major in the Grenadier Guards. He was killed in action in Tunisia during World War II. Let us note that the aristocratic Evelyn family were descended from the famous diarist John Evelyn (1620-1706).John Evelyn, the subject of this biography, was known to his friends as Jack. Like his father, he attended Eton College, the famous independent school in Windsor, Berkshire, England founded in the mid-fifteenth century. It was at Eton that Evelyn became fascinated by mathematics, particularly by number theory and geometry. He decided to study mathematics at university and, continuing to go to the same educational institutions as his father, he matriculated at Christ Church, University of Oxford. He graduated with a B.A. in 1927. At Oxford he had become friendly with Hubert Linfoot who was one year older than Evelyn. Linfoot graduated in 1926 but had remained at Oxford undertaking research advised by G H Hardy. Both Evelyn and Linfoot were interested in number theory at this time and they worked together on some problems which we now describe.
Between 1929 and 1933, Evelyn and Linfoot produced six joint papers, all with the title On a problem in the additive theory of numbers. These concerned -free integers:
If ≥ 2, then an integer is called -free if it is not divisible by the th power of any prime.
In the first of their joint papers, On a problem in the additive theory of numbers (1929), they found an asymptotic formula, with estimation of the remainder, for the number of representations of a large integer as the sum of -free integers. They improved and extended their results in five later papers (making six in total). Among the variants to this problem they studied in these later papers, we mention that of determining the asymptotic behaviour, as tends to infinity, of the number of representations of as the sum of -free integers which are congruent to (mod ). These problems continue to be of interest to number theorists and among the papers which contain results that extend and improve of those of Evelyn and Linfoot we list six below, namely [2], [3], [5], [6], [7], and [8].
Evelyn had no need to look for employment since his family fortune provided him with an income which allowed him to live the life of a gentleman of leisure devoting himself to those pursuits that interested him. He had many interests other than mathematics and we shall say a little about these below. First we continue to describe his contributions to mathematics. After the joint papers with Linfoot, Evelyn did not publish any further mathematics papers for over 30 years. He began to produce further work in the mid-1960s. His papers from that time are: A relationship for the Möbius function (1966); (with Theodore William Chaundy) Some inequalities (1967); Relations between arithmetical functions (1967); (with J A Carroll and R Cordner) A new extension of Hölder's inequality (1970); and (with D R Heath-Brown) Arithmetical functions and inversion formulae (1974). Note that this was David Rodney "Roger" Heath-Brown's first paper. He has, to date, published over 170 items listed in Mathematical Reviews. We also note Evelyn's address on his papers. In his papers with Linfoot, he gives his address as 'Wotton'. [Wotton is in Surrey, England.] In the 1966 and 1967 papers he gives his address as 'St James' Club, Piccadilly, London'. In 1974 he gives '33 Grosvenor Square, London'.
A book was to be Evelyn's final mathematical publication. He published the book (with G B Money-Coutts and J A Tyrrell) The seven circles theorem and other new theorems (1974) which was translated into French and published as (with G B Money-Coutts and J A Tyrrell) Le théorème des sept cercles (1975). R D Nelson, Ampleforth College, York, writes [4]:-
This elegant book will please all geometers, amateur and professional, and deserves a place in every library. Using a variety of essentially elementary methods, the authors present and prove a number of new or little known theorems in plane geometry. To emphasise the aesthetic appeal of these results and to assist the argument in places, over forty of its pages carry diagrams of high quality. The book has three independent sections but the style of writing is uniform. The authors invite and sometimes require the co-operation of the reader as he works through the book and, in this way, they prepare him for the intricacies of the final and most difficult section. The first part re-introduces an algebra of vectors, due to Silberstein, in which the laws of addition and equivalence are such that few of the usual properties are obvious. For example, associativity of addition requires two applications of Desargues' theorem for its proof. No use is made of this algebra. The second section opens with a delightful new theorem concerning seven Pascal lines derived from a heptagon inscribed in a conic. This is followed by a number of extensions and generalisations of the theorems of Pascal and Brianchon. ... Finally there are four new theorems about closed chains of six circles ... In the first theorem each circle touches a seventh, in the second the circles alternately touch a pair of parallel lines, in the third each circle touches two of the sides of a triangle and in the fourth each circle touches two out of three fixed circles making a configuration of nine circles in all. The first theorem, beautifully proved by inversion, gives the book its title.
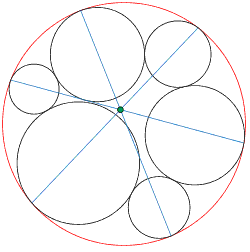 The remarkable thing about this book is that the theorem of the title is an elementary geometry theorem which appears to have been first discovered by the authors of this book. The theorem concerns six circles, all inside and touching a seventh circle. These six circles all touch each other. Join each of the six points on the outer circle where the six inner circles touch it, to the point of contact directly opposite it. The theorem states that these three lines are concurrent.
The remarkable thing about this book is that the theorem of the title is an elementary geometry theorem which appears to have been first discovered by the authors of this book. The theorem concerns six circles, all inside and touching a seventh circle. These six circles all touch each other. Join each of the six points on the outer circle where the six inner circles touch it, to the point of contact directly opposite it. The theorem states that these three lines are concurrent.
We mentioned above that Evelyn had many interests in addition to mathematics. In fact [9]:-
... loved to travel (and did so regularly for the greater part of his life), and he loved to write; he produced many books of poetry, written in a lyrical style very reminiscent of Swinburne, and a number of prose works that reveal, among other things, his great curiosity about matters supernatural.As to poetry he published Poems (1937), Aena, and other poems (1938), The Wanderer. Poems (1950), Pandora. Poems (1954), A book of poems (1956). He also wrote Fortuna, and new lyrics (1936), The comedy of Faust (a verse play) (1959), The tragedy of Faustus (a verse play) (1959), and Walpurgis Nacht (a verse play) (1961). Finally we mention the intriguing The Dupont Theory. The theory of gravitation in mental fields ... An essay on the nature of human understanding ... (1957).
His two plays about Faust, one called a comedy and the other a tragedy, need a little explanation. We quote from Eric A Blackwell, writing in [1]:-
The play [Faust] is difficult to interpret and inconclusive. Evelyn called it a tragedy "to mislead the readers," as he says in his Preface. The questions remain questions, but they are basically concerned with tension between contemplation of possibilities and the specific actualities of choice and action. Evelyn later produced a 'Comedy of Faust'. The tragedy, if it had been finished, was to have had a happy ending, he tells us. These two plays, taken together, suggest that the drama could have ended either way.Evelyn had other interests as we are told in [9]:-
He also had a consuming passion for music, and was never happier than when entertaining his friends at the opera or ballet; I know that I share, with many members of the London Mathematical Society, the most delightful memories of evenings that he organised at the Royal Opera House. His generosity, however, was not only enjoyed by individual members; the Society as a whole was always close to his heart, and he demonstrated this by the many gifts of books and journals that he presented to the Library over the years; no one who uses the Library at all regularly can have failed to notice the extent of these donations.Tyrrell sums up Evelyn's character as follows [9]:-
In his mathematics, as in everything else, Jack Evelyn was not a man to follow fashions. He did what he did because he enjoyed doing it. His mathematical interests were fairly closely circumscribed and, perhaps for that reason, one did not get to know him very easily; but his friendship, once given, was a lasting one and its loss, to those of us who knew it, will not easily be forgotten.He died after suffering a painful illness over several years. A 'Service of Remembrance and Thanksgiving' was held on Wednesday, 30 June 1976, in St James's Church, Piccadilly, London.
References (show)
- P Boerner and S Johnson (eds.), Faust through Four Centuries - Vierhundert Jahre Faust: Retrospect and Analysis - Rückblick und Analyse (Walter de Gruyter, 1989).
- L Mirsky, On a theorem in additive number theory due to Evelyn and Linfoot, Mathematical Proceedings of the Cambridge Philosophical Society 44 (3) (1948), 305-312.
- L Mirsky, Generalization of some results of Evelyn-Linfoot and Page, Nieuw Arch. Wiskunde (2) 23 (1950), 111-116.
- R D Nelson, Review: The seven circles theorem and other new theorems, by C J A Evelyn, G B Money-Coutts and J A Tyrrell, The Mathematical Gazette 60 (412) (1976), 148-149.
- C Pomerance and D Suryanarayana, On a problem of Evelyn-Linfoot and Page in additive number theory, Publ. Math. Debrecen 26 (3-4) (1979), 237-244.
- R S R C Rao and G Murty, Sri Rama Chandra On a problem of Evelyn and Linfoot in the additive theory of numbers, Indian J. Math. 24 (1-3) (1982), 205-208.
- R Sitaramachandra Rao and G Sri Rama Chandra Murty, On Mirsky's generalisation of a problem of Evelyn-Linfoot and Page in additive theory of numbers, J. Reine Angew. Math. 309 (1979), 92-99.
- D Suryanarayana and V Sita Ramaiah, Generalization of a problem of Evelyn-Linfoot and Page in additive number theory, Ann. Mat. Pura Appl. (4) 126 (1980), 1-17
- J A Tyrrell, Cecil John Alvin Evelyn, Bull. London Math. Soc. 9 (3) (1977), 328-329.
Additional Resources (show)
Other websites about John Evelyn:
Written by J J O'Connor and E F Robertson
Last Update April 2015
Last Update April 2015
