Guo Shoujing

Quick Info

Born

1231
Xingtai, Hebei province, China

Died

1316
China

---

Summary

Guo Shoujing was a Chinese astronomer who worked on spherical trigonometry and the calendar.

Biography

Guo Shoujing is also known as Kuo Shou-ching. We do not know the names of his parents, but his paternal grandfather, who was clearly more famous than his parents, was Guo Yong who was famed as an expert in a wide range of topics from classical studies to mathematics and hydraulics. One can only guess that as a young boy Guo might have been influenced by his grandfather to become interested in constructing water clocks. We know that at age 14 Guo did construct such a clock. He designed a lotus clepsydra, that is a water clock which had a bowl shaped like a lotus flower on the top into which water dripped. By the age of sixteen Guo was studying mathematics.

Before we continue to describe events of Guo's life we should look briefly at the political situation, for it was a troubled time with many wars. After the death of Genghis Khan, one of his sons Ogodei had become the Great Khan in 1229. He had expanded the Mongol empire sending armies to complete the defeat of the Jurchens. By 1234 the Mongols had completed the destruction of the Jurchen empire and turned their attention to the south. This then was the situation in the northern part of China where Guo was growing up. By the age of twenty Guo was working as an hydraulic engineer. In 1251, as a government official, he worked on a project to repair an old bridge over the river Dahuoquan. This was a river in Guo's home province of Hebei and the bridge he renovated was a little way north of the town of Xinzhou.

Kublai, a grandson of the Mongol leader Genghis Khan began leading further Mongol advances in the latter years of the 1250s. On 5 May 1260 Kublai was elected Khan at his residence in Shang-tu and he began to organise the country. Zhang Wenqian, who was a friend of Guo and like him was a central government official, was sent by Kublai Khan in 1260 to Daming where unrest had been reported in the local population. Guo accompanied Zhang on his mission. Guo was not only interested in engineering, but he was also an expert astronomer. In particular he was a skilled instrument maker and understood that good astronomical observations depended on expertly made instruments. He now began to construct astronomical instruments, including water clocks for accurate timing and armillary spheres which represent the celestial globe.

Zhang advised Kublai Khan that his friend Guo was a leading expert in hydraulic engineering. Kublai knew the importance of water management, for irrigation, transport of grain, and flood control, and he asked Guo to look at these aspects in the area between Dadu (now Beijing or Peking) and the Yellow River. To provide Dadu with a new supply of water, Guo found the Baifu spring in the Shenshan Mountain and had a 30 km channel built to bring the water to Dadu. He proposed connecting the water supply across different river basins, built new canals with many sluices to control the water level, and achieved great success with the improvements which he was able to make. This pleased Kublai Khan and led to Guo being asked to undertake similar projects in other parts of the country. In 1264 he was asked to go to Gansu province to repair the damage that had been caused to the irrigation systems by the years of war during the Mongul advance through the region. Guo travelled extensively along with his friend Zhang taking notes of the work which needed to be done to unblock damaged parts of the system and to make improvements to its efficiency. He sent his report directly to Kublai Khan.

The advance of the Monguls was continuing under Kublai Khan and in 1276 he captured the city today named Hangzhou south of Shanghai. For many years the need for calendar reform had been understood but Kublai Khan saw political benefits in bringing in a new calendar at this time to emphasise how the new regime was replacing the old. Asked for his advice, Guo explained that:-

... the fundamental method is to carry out observation and tests in the area of astronomical changes.

Guo, together was Wang Xun, were asked to set up a special bureau to undertake the necessary research and to make proposals for the new calendar. An accurate calendar depends on the quality of the astronomical data used to support it and Guo's first move was to built seventeen new astronomical instruments so that accurate data could be collected. Of these seventeen instruments, thirteen were to be set up in an observatory in Kublai's capital Dadu (today called Beijing or Peking) while the other four were portable instruments which could make observations from different locations.

Let us briefly describe an improvement Guo made in constructing one such instrument. The simplest astronomical instruments was the gnomon, nothing other than a stick which was erected and the length of its shadow measured. The minimum length of shadow during a day is less in summer than in winter and at the solstices it changes from lengthening to shortening or visa versa. To make it easier to determine these points Guo fixed a crossbar to the top of a gnomon and used the principle of the pinhole camera to cast its shadow onto a measuring scale.

Kublai Khan established an Astronomical Observatory in Beijing in 1279. Building began in March of that year and, following a design proposed by Guo, the work was completed in two months. Guo's friend Zhang Wenqian was appointed as director and Guo together with his colleague Wang Xun were the two co-directors. Making sense of the data gathered from the instruments required a knowledge of spherical trigonometry and Guo devised some remarkable formulae. We look below at the clever mathematics which he introduced in undertaking his project on the new calendar.

The work was completed by 1280, Guo having calculated the length of the year correct to within 26 seconds, and in the following year Kublai Khan introduced the use of this extremely accurate calendar. It remained in use for 364 years. Zhang Wenqian died in 1283 and Guo was promoted to be director of the Observatory in Beijing. In 1292, in addition to his role of director of the Observatory, he was made head of the Water Works Bureau. He now undertook major projects designing a canal system to link the capital with other major towns. As always he met with success and even after the death of Kublai Khan, although Guo was by this time an old man, his advice continued to be sought by Kublai's successor.

We should now look at the rather remarkable work which Guo did on spherical trigonometry and solving equations. He produced a number of formulae for triangles, two sides of which were straight lines and the third was the arc of a circle. These formulae are approximate ones, but Guo was well aware of this. In a sense approximation was not regarded as important by the Chinese and they never became obsessed by the "squaring the circle" type of question like the ancient Greeks, since the Chinese approach was more practical and never axiomatic.

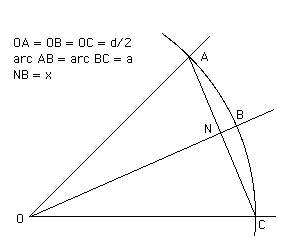
In the diagram $d$ is the diameter of the circle, $a$ is the length of the arc $AB$ and $x$ is the length of $NB$ which Guo wanted to calculate. He gave the approximate formula

$x^{4} + (d^{2} - 2ad)x^{2} - d^{3}x + a^{2}d^{2} = 0$.

To solve this equation Guo used a numerical method similar to Horner's method. The equation has two real roots, the smaller being the solution to the problem while the other, being numerically larger than the length of the arc, was rightly discarded by Guo.

There is a fascinating fact relating to this work which it is interesting to investigate. Two of the coefficients of the equation, namely the constant term and the coefficient of $x^{2}$, involve the length $a$ of the arc, so require a value to be chosen for π. Guo takes π = 3 which at first sight seems strange since much more accurate values were known in China at the time that Guo was doing his calculations. For example $\large\frac{22}{7}\normalsize$ was known to be more accurate and $\large\frac{355}{113}\normalsize$ , given by Zu Chongzhi, was known to be more accurate still. Why did Guo choose π = 3? Surprisingly this gives a better answer than the more accurate values of π, for remember the formula is itself based on approximations. One has to believe that Guo chose π = 3 because he knew that the answers that he then found for different sizes of the angle at $O$ more closely approximated values he found by direct measurement.

Here is a computation from a computer algebra system which illustrates the point. The values are computed for increasing angles up to 90° for a circle of radius 100. The first column is the value of $x$ using Guo's formula taking an accurate modern approximation to π, the second column is the result given by the formula with π = 3, while the third column is the correct answer calculated using trigonometry (in fact the cosine).

Guo's formula    Guo's formula    Correct 
formula with     formula with     answer  
correct π        π = 3 

  1.2401831       1.1304311       1.2311659
  5.0213452       4.5732560       4.8943483
 11.4521976      10.4253695      10.8993475
 20.5459874      18.7159078      19.0983005
 32.0790854      29.2893218      29.2893218
 45.5479024      41.7514260      41.2214747
 60.2936574      55.5434416      54.6009500
 75.7085631      70.1045733      69.0983006
 91.3723645      85.0063893      84.3565534
107.0799476     100.0000000     100.0000000

Guo used other clever mathematical techniques in his calculations for the calendar. He would interpolate values between his data points and he did this using a cubic interpolation formula. The reason that interpolation was required was that the motion of the sun through the stars throughout the year is irregular. This was discovered by Chinese astronomers in the sixth century. Guo looked at the accumulated difference, namely the difference in degrees moved by the sun in a day compared with the expected degrees moved if the motion was constant. He then tabulated first, second, and third differences of the accumulated difference as in Newton's forward difference interpolation method.

References (show)

1. Biography in Ke Shaomin, Xin Yuanshi (New Official History of the Yuan Dynasty).
2. J-C Martzloff, A history of Chinese mathematics (Berlin-Heidelberg, 1997).
3. J-C Martzloff, Histoire des mathématiques chinoises (Paris, 1987).
4. J Needham, Science and Civilisation in China 3 (Cambridge, 1959).
5. K Yabuuti (trans. Benno van Dalen), Islamic astronomy in China during the Yuan and Ming dynasties, Historia Sci. (2) 7 (1) (1997), 11-43.
6. H P Yoke and M Wang, Kuo Shou-ching, in I de Rachewiltz et al. (eds.), In the Service of the Khan : Eminent Personalities of the Early Mongolian Period (1200 -1300) (Wiesbaden, 1993), 282 -299.

Additional Resources (show)

Other pages about Guo Shoujing:

1. Miller's postage stamps

Honours (show)

Honours awarded to Guo Shoujing

1. Lunar features Crater Kuo Shou Ching

Cross-references (show)

1. History Topics: Overview of Chinese mathematics
2. Other: Jeff Miller's postage stamps

Written by J J O'Connor and E F Robertson
Last Update December 2003