Christian Heinrich von Nagel
Quick Info
Stuttgart, Germany
Ulm, Germany
Biography
Christian Heinrich von Nagel's parents were Johann Heinrich Nagel, who was a tailor, and Christiane Friedrike Huntzinger. The family was poor and Johann Heinrich Nagel wanted his son to follow in his profession of tailor. However, two people helped Christian Heinrich to receive an education. First there was his maternal grandfather who was an educated man and gave the young boy his first lessons. Second there was August von Weckherlin (1794-1868), an agronomist born in Stuttgart who was a good customer of Nagel's father. He persuaded the Nagel family to allow their son to study. For someone with no means of financial support there was little choice at this time in what one could study. The only route to an education was through the church and this is the route Christian Heinrich took.Nagel attended classes at the Gymnasium in Stuttgart and then after taking the county examinations in 1817 he was accepted into the Evangelical Seminaries of Maulbronn and Blaubeuren in Baden-Württemburg. These two Protestant Gymnasiums had been founded in the middle of the 16th century to provide a broad education to gifted pupils. They were boarding schools with the younger boys going to Maulbronn and then transferring to Blaubeuren. Nagel studied in these Gymnasiums for four years and, although the aim was an education based on theology, he also studied science and mathematics at Blaubeuren. He soon realised that he had a passion for mathematics.
In 1821 he entered the Evangelical Monastery in Tübingen and began his studies of theology at the Eberhard-Karls University of Tübingen. However he also attended lectures on mathematics and physics at the university given by the astronomer Johann Gottlieb Friedrich von Bohnenberger (1765-1831), who was the professor of mathematics and astronomy at the University of Tübingen, and Friedrich Joseph Pythagoras Riecke (1794-1876) who was a lecturer in Tübingen until 1823 when he left to become Professor of Mathematics and Physics in Hohenheim. Nagel had hoped to study under Christoph Friedrich von Pfleiderer, professor of mathematics at Tübingen, but Pfleiderer died in September 1821 just when Nagel was starting his studies.
Nagel completed his studies in 1825 and, having qualified as a clergyman, entered the Church. His first church was in Kirchentellinsfurt, about 7 km east of Tübingen and later he moved to the church in Hengen about 30 km south east of Tübingen. While in Hengen he applied for a teaching position in Oldenburg but he was not successful. In December 1826 he applied for a teaching position at the Lyceum in Tübingen. He was accepted and began teaching both there and at the Realschule in Tübingen in 1827. He taught both mathematics and biology at these schools. Being in Tübingen, he took the opportunity to continue his study of mathematics at the university. Advised by Bohnenberger, he submitted his thesis De triangulis rectangulis ex algebraica aequatione construendis Ⓣ to the Faculty of Arts of the University of Tübingen in October 1827 and was appointed as a privatdocent. At the University he lectured on Euclidean geometry and on mathematical and physical geography.
When Nagel realised that his chances of becoming a professor at Tübingen were very slight, he decided to accept the offer of an appointment as Professor of Mathematics and Natural Science at the Gymnasium in Ulm. He took up this position on 1 November 1830 and at the same time he taught at the Realschule in Ulm. In September 1844 he became Rector of the Real-Schule in Ulm and he continued to hold this position for 25 years. He retired from teaching in 1875. As to Nagel's approach to teaching mathematics we note that he writes in his book Die Idee Der Realschule, Nach Ihrer Theoretischen Begründung Und Praktischen Ausführung Dargestellt Ⓣ (1840) that an education in mathematics is necessary:-
... to expose the ideas laid down in nature: the simple pure utterances of the deity.Nagel published six mathematical articles, the most important of which is Untersuchungen über die Eigenschaften der wichtigsten mit dem Dreieck in Verbindung stehenden Kreise Ⓣ (1835) and Untersuchungen über die wichtigsten zum Dreiecke gehörigen Kreise. Eine Abhandlung aus dem Gebiete der reinen Geometrie Ⓣ (1836). In these papers he studied various points in a triangle which occur as the intersection of concurrent lines. He is most famous for one of these points of intersection that is today called the Nagel point.
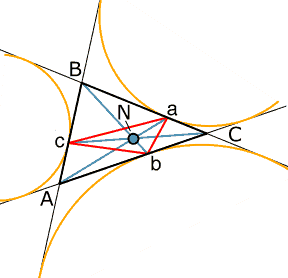
This is constructed in a simple way. Take any triangle and let be its semiperimeter, this is half the sum of the lengths of the three sides. Starting at go a distance round the triangle to a point on that we will call . Similarly starting at go a distance round the triangle to a point on that we will call and starting at go a distance round the triangle to a point on that we will call . Then the lines are concurrent at , the Nagel point.
There is another way to construct and since they are the points where the three excircles touch the triangle as shown in the diagram.
There is another way to construct and since they are the points where the three excircles touch the triangle as shown in the diagram.
Particularly interesting is Nagel's idiosyncratic, purely elementary geometrical method of proof. In his papers he proved the existence of the Nagel point and other points such at the Gergonne point and the Middle point. The Middle point of a triangle is the point where the three lines, each formed by joining the centre of an excircle to the midpoint of the side of the triangle that it touches, concur. The Gergonne point is the point where the three lines, each formed by joining the point the incircle touches a side to the opposite vertex, concur. Other interesting properties of the Nagel point is that it, the centroid and the incentre of a triangle are collinear.
Other mathematical publications by Nagel include Theorie der periodischen Decimalbrüche nebst Tabellen zur leichteren Verwandlung gewöhnlicher Brüche in Decimalbrüche Ⓣ (1845).
Nagel made other contributions to Ulm in addition to serving as a teacher and rector there. In particular he acted as an advisor to the city magistrates and it was Nagel who was instrumental in setting up gas lighting in Ulm. He was also responsible for setting up a technical training school to provide commercial training to pupils. Another of his achievements was founding a mathematical club in Ulm.
References (show)
- P Baptist, Historische Anmerkungen zu Gergonne- und Nagel-Punkt, Sudhoffs Archiv 71 (2) (1987), 230-233.
- P Baptist, Nagel, Christian Heinrich von, Neue Deutsche Biographie 18 (1997), 709-710.
- Christian Heinrich von Nagel, Allgemeine Deutsche Biographie 23 (1886), 214.
- R H Eddy and R Fritsch, The Conics of Ludwig Kiepert: A Comprehensive Lesson in the Geometry of the Triangle, Mathematics Magazine 67 (3) (1994), 188-205.
Additional Resources (show)
Other websites about Christian Heinrich von Nagel:
Written by J J O'Connor and E F Robertson
Last Update October 2015
Last Update October 2015
