Curves
Cassinian Ovals
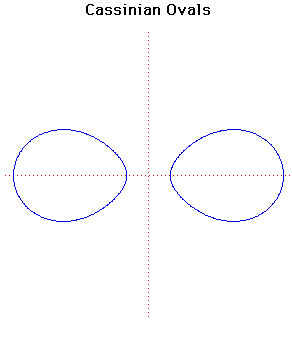
- Cartesian equation:
Description
The Cassinian ovals are the locus of a point that moves so that the product of its distances from two fixed points and [in this case the points ] is a constant. The shape of the curve depends on . If then the curve consists of two loops. If then the curve consists of a single loop. The case where produces a Lemniscate of Bernoulli (a figure of eight type curve introduced by Jacob Bernoulli ).The curve was first investigated by Giovanni Cassini in 1680 when he was studying the relative motions of the Earth and the Sun. Cassini believed that the Sun travelled round the Earth on one of these ovals, with the Earth at one focus of the oval. Cassini actually introduced his curves 14 years before Jacob Bernoulli described his lemniscate.
Cassinian Ovals are anallagmatic curves. They are defined by the bipolar equation .
Even more incredible curves are produced by the locus of a point the product of whose distances from 3 or more fixed points is a constant.
Other Web site:
Xah Lee