Curves
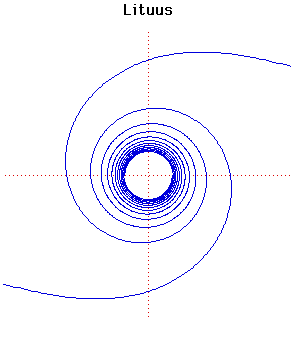
Lituus
Description
The lituus curve originated with Cotes and is described in his book Harmonia Mensurarum (1722). Lituus means a crook, for example a bishop's crosier. Maclaurin gave the curve its name in 1722. The lituus is the locus of the point moving in such a manner that the area of a circular sector remains constant.Roger Cotes (1682-1716) died at the age of 34 having only published two memoirs during his lifetime. Appointed professor at Cambridge at the age of 24 his work was published only after his death.
Cotes discovered an important theorem on the th roots of unity; anticipated the method of least squares and discovered a method of integrating rational fractions with binomial denominators.