Curves

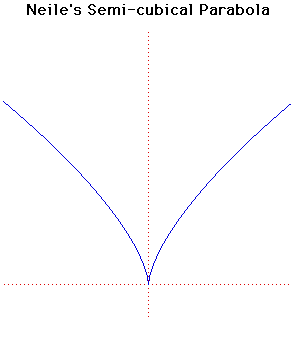
Neile's Semi-cubical Parabola

Description

This curve, sometimes called the semi-cubical parabola, was discovered by William Neile in 1657. It was the first algebraic curve to have its arc length computed. Wallis published the method in 1659 giving Neile the credit. The Dutch writer Van Heuraet used the curve for a more general construction.

William Neile was born at Bishopsthrope in 1637. He was a pupil of Wallis and showed great promise. Neile's parabola was the first algebraic curve to have its arc length calculated; only the arc lengths of transcendental curves such as the cycloid and the logarithmic spiral had been calculated before this. Unfortunately Neile died at a young age in 1670 before he had achieved many further results.

In 1687 Leibniz asked for the curve along which a particle may descend under gravity so that it moves equal vertical distances in equal times. Huygens showed that the semi-cubical parabola $x^{3} = ay^{2}$ satisfied this property. Because of this it is an isochronous curve.

The semi-cubical parabola is the evolute of a parabola.

Other Web site:

Xah Lee

Associated Curves

Definitions of the Associated curves

Evolute

Involute 1

Involute 2

Inverse curve wrt origin

Inverse wrt another circle

Pedal curve wrt origin

Pedal wrt another point

Negative pedal curve wrt origin

Negative pedal wrt another point

Caustic wrt horizontal rays

Caustic curve wrt another point