Curves
Cycloid
Description
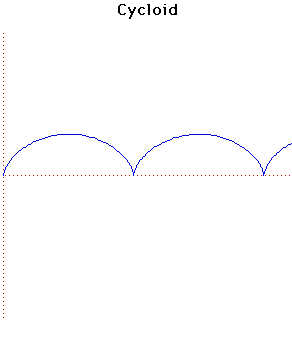
The cycloid is the locus of a point at distance from the centre of a circle of radius that rolls along a straight line. If it is a curtate cycloid while if it is a prolate cycloid. The curve drawn above has .The cycloid was first studied by Cusa when he was attempting to find the area of a circle by integration.
Mersenne gave the first proper definition of the cycloid and stated the obvious properties such as the length of the base equals the circumference of the rolling circle. Mersenne attempted to find the area under the curve by integration but failed. He posed the question to other mathematicians.
The curve was named by Galileo in 1599. In 1639 he wrote to Torricelli about the cycloid, saying that he had been studying its properties for 40 years. Galileo attempted to find the area by comparing its area to that of the generating circle. After he failed to find a mathematical method he resorted to weighing pieces of metal cut into the shape of the cycloid. He found that the ratio of the weights was approximately 3 to 1 but decided that it was not exactly 3, in fact he guessed (wrongly) that the ratio was not rational.
Mersenne proposed the problem of the area to Roberval in 1628 and, although he failed at first, it was solved by Roberval in 1634. If then the area under an arch is . Roberval, proud of his result, wrote to Descartes telling him of it. Descartes replied that the result was
a pretty one which I had not noticed before but which would cause no difficulty to any moderately skilled geometer.
Descartes challenged Roberval to find a method of drawing a tangent to the cycloid having discovered himself how to construct one. Roberval failed but Fermat, who was included in the challenge, succeeded.
It is worth noting that Torricelli independently discovered the area of the cycloid and Viviani independently found a method for constructing a tangent.
In 1658 Pascal, after a long spell devoted to religion when he ignored mathematics, started to think about mathematical problems again as he lay awake at night unable to sleep for pain. He solved the problem of the area of any segment of the cycloid and the centre of gravity of any segment. He also solved the problems of the volume and surface area of the solid of revolution formed by rotating the cycloid about the -axis.
Pascal published a challenge (not under his own name but under the name of Dettonville) offering two prizes for solutions to these problems. Wallis and Lalouère entered but Lalouère's solution was wrong and Wallis was also not successful. Sluze, Ricci, Huygens, Wren and Fermat all communicated their discoveries to Pascal without entering the competition. Wren's contribution was the most remarkable as he found the arc length, the length of the arch being 8a.
Pascal published his own solutions to his challenge problems together with an extension of Wren's result which he was able to find.
The cycloid has the property that a particle sliding on a cycloid will exhibit simple harmonic motion and the period will be independent of the starting point. This is the tautochrone property and was discovered by Huygens in 1673 (Horologium oscillatorium). He constructed the first pendulum clock with a device to ensure that the pendulum was isochronous by forcing the pendulum to swing in a cycloid arc. However this presents too many mechanical problems to make it practical.
Desargues proposed cycloidal teeth for gear wheels in the 1630's.
In 1696 Johann Bernoulli, in Acta eruditorum, asked which curve satisfies the brachistochrone property. He already knew the brachistochrone property of the cycloid and published his solution in 1697. It was also shown by Leibniz, Newton, Bernoulli and de L'Hôpital. It was one of the earliest variational problems and its investigation was the starting point for the development of the calculus of variations.
The caustic of the cycloid, where the rays are parallel to the -axis is a cycloid with twice as many arches.
Both the evolute and involute of a cycloid is an identical cycloid. In fact the evolute was studied by Huygens and because of his work on the cycloid Huygens developed a general theory of evolutes of curves.
Other Web sites:
Xah Lee
Harare, Zimbabwe