John Marshall
Mr John Marshall, Scholar of Trinitywas described in the preface to On Growth and Form as a much younger but very helpful friend.
John Marshall was a St Andrews alumnus, and later a lecturer in mathematics. During the First World War he worked as an Orderly in a Military Hospital. There are quite a few letters indicating meetings between Marshall and D'Arcy, where Marshall helped him with mathematical problems (including log-spirals, Miraldi pyramids of bees cells and so on). Later letters indicate that Marshall also made some corrections to the Geodetics chapter and the Logarithmic spiral chapter, the latter of which Thompson did not
yet fully understand(ms17247). Hence, there is no way of knowing the full extent to which Marshall influenced Thompson's mathematical knowledge.
During WW1, Marshall could not help D'Arcy anymore, because of the hardships he faced. Marshall was afraid that he would be called for service in the army and had to work as an orderly in a Military hospital in York. He was asking D'Arcy's help to avoid service in the army. However, D'Arcy did not help Marshall. Instead he suggested other people whom Marshall could ask for help. Marshall implied that Thompson held quite pro-militaristic views.(ms15255-ms15258).
Coordinate transformations
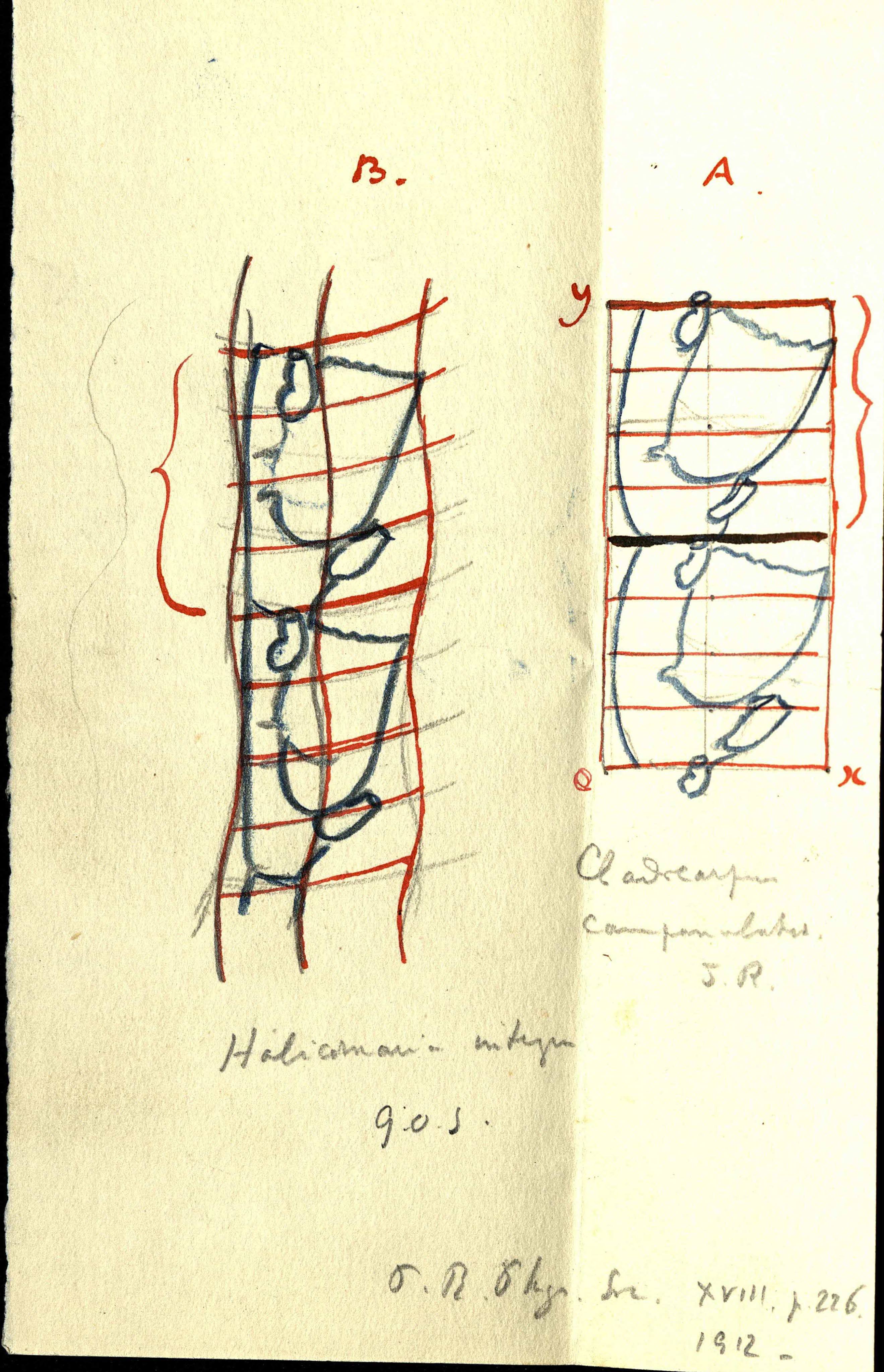
Thompson's drawing in the letter ms45792 |
|
One of the most interesting letters in Thompson's - Marshall's correspondence is about coordinate transformations (ms45792). Thompson sends an image of two figures of hydroids, A drawn into regular cartesian coordinates and B, which is a transformation of A (Figure 1). Then sets up a four step way to get such transformation and asks a question:
Will it, or not, be the case, that, if we had begun by drawing B instead of A in regular coordinates then the expansion for its transformation with A would be the same, only with change of sign, that we have got for the curving of A into B?
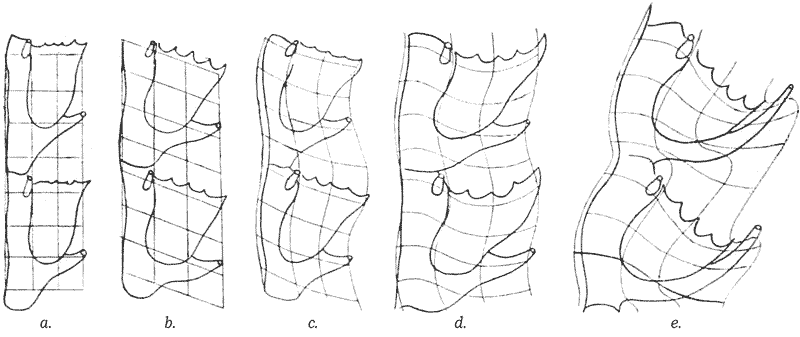
It is also interesting to note that the same drawing later appears in the book itself (Figure 2).
Marshall replies by saying that, in general, it would not be the case, and then he goes through the set up and explains why it would not work in the given cases.
For example if the transformation is x=aX and y=bY (where (x,y) - point in the original coordinates, and (X,Y) - in the new ones and a,b - are constants) then the reverse would be X=x/a and Y=y/b.
(for those interested, see here for the full transcript).
However, it is not clear how much D'Arcy understood of this reply, because in the following letter he says that there are points in it which he still cannot grasp. (ms17247)
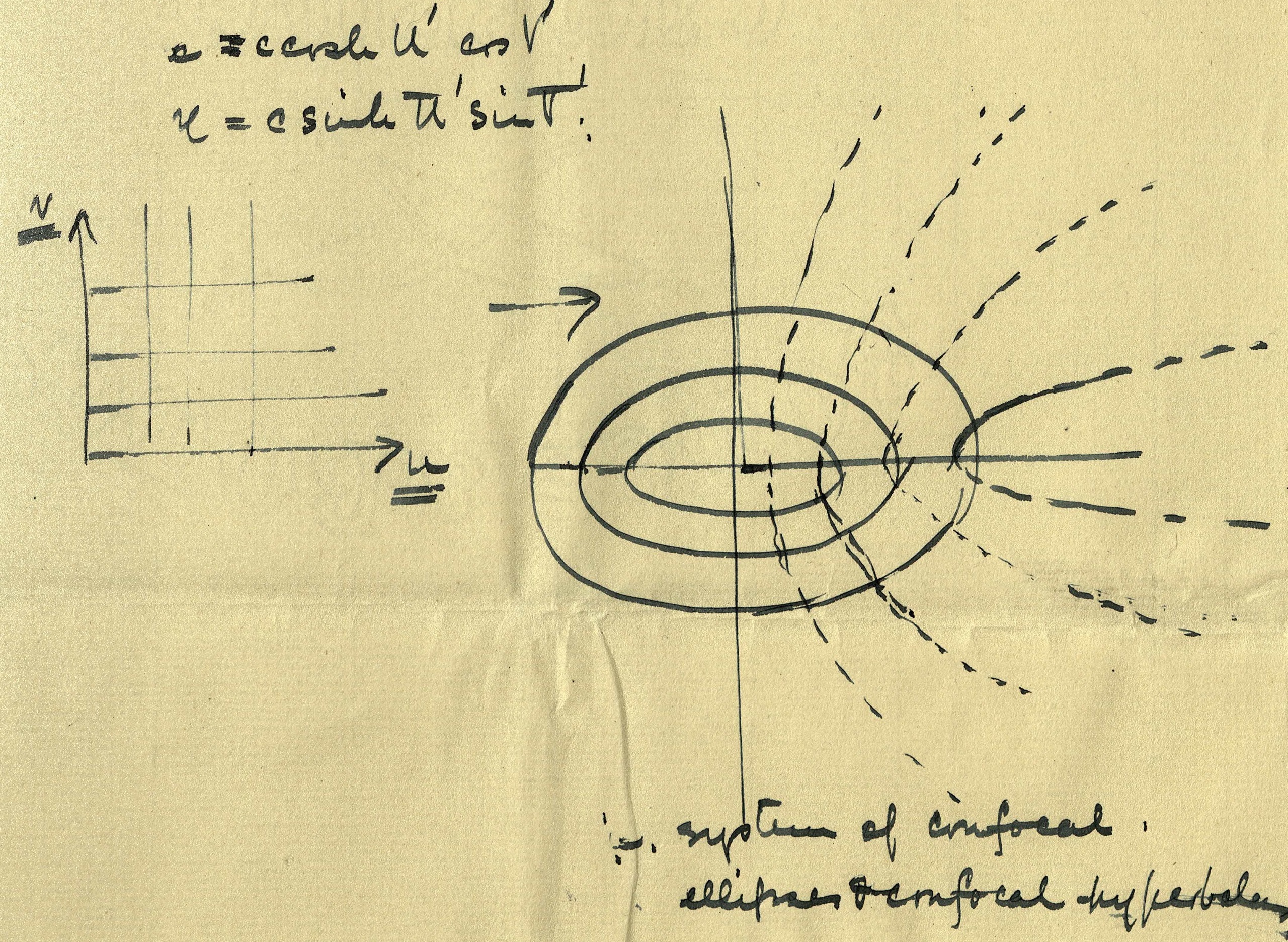
|
Back to the Transformations
Eric Harold Neville
Alfred North Whitehead