E H Neville
Correspondence with Neville (3D Coordinates)
Eric Harold Neville (1889-1961) was an English mathematician whose main area of expertise was in the field of geometry. He is best known for his book on Jacobian Elliptic Functions and his development of geometrical methods in four dimensions.
He corresponded with D'Arcy Thompson during 1915, two years before On Growth and Form was published. Their letters mainly discuss 3-dimensional coordinate systems.

|
|
In On Growth and Form, there is a small section at the end of the chapter on Transformations which mentions the use of 3-dimensional coordinate systems. Thompson deals only with 2D coordinates when discussing co-ordinate transformations throughout the chapter as he struggles with the mathematics of 3D coordinates. On the topic of 3 dimensions he says:
…this extended theme I have not attempted to pursue, and it must be left to other times, and to other hands.
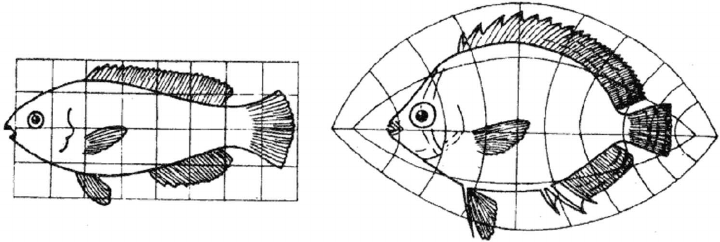
D'Arcy uses the simple case of fishes to explain his problem to Neville using the 'Round' Haddock and 'Flat' Plaice as examples. However, it is less accurate to express the required transformations using only 2D as it is a 3D problem. The main difficulties lie in the position of the eyes and the number of fins.
The transformation is seen through the broadening (increasing along y-axis) and flattening out (z diminishing) of the plaice's body. Both change relatively to the x direction. Here the breadth and depth vary inversely and this is seen in several other fish examples.
The weight-length coefficient in fishes is given by W = kL3, with constant k practically identical in both the haddock and plaice. In On Growth and Form Thompson concludes,
the extent to which the plaice has broadened is just about compensated for by the extent to which it has also got flattened or thinned.
Thompson asks Neville for help with his biological problems in terms of 3D coordinates which he is
incapable of tacklinghimself. Using the haddock-plaice example, he asks Neville if he can illustrate the flattening process using x,y and z coordinates and enquires what the xz and yz diagrams would show if flattened according to respective xy diagrams.
From this, it is clear that D'Arcy consulted with Neville on this topic but there is little evidence to show how much Neville influenced D'Arcy's thinking on 3D coordinates. The section at the end of the book lacks detail on how 3D transformations work and instead highlight Thompson's lack of understanding.
Back to the Transformations
John Marshall
Alfred North Whitehead