Gibson History 4 - John Napier
In the Napier Tercentenary Memorial Volume Napier's achievements are so fully and interestingly set forth that I may confine myself to a short statement on one or two of the more salient topics. The conditions prevailing in Napier's day are graphically presented by Professor Hume Brown in his sketch and the following extract is instructive:-
"Even to-day a certain mystery surrounds the figure of the Laird of Merchiston. Appearing at the time he did, and in an environment seemingly so strangely in contrast with his special pursuits, he strikes us as the most singular of apparitions among his contemporaries. He had one fellow-countryman, indeed, as a predecessor in the study of physical science. In the thirteenth century Michael Scott, like his contemporary Roger Bacon, had given his attention to that study; had gained a continental reputation as wide as Napier's, and an equally evil name among his countrymen of being in league with the infernal powers. But between Michael and Napier we can name no Scot whose interest lay specially in the domain of science, and the explanation is simple. In Scotland, as in other countries, the universities were the exclusive centres of intellectual activity, and the studies at the Universities were under the sole dominion of the Church, which naturally laid its ban on investigations that might imperil its own teaching. By his isolation Napier is thus wrapped in a certain mystery, and the mystery is deepened by the fact that we know so little of him, and that what we do know is at times strangely incongruous with the main preoccupations of his life" (Mem. Vol., p. 34).
John Napier was born in 1550 at Merchiston Castle, near Edinburgh. Of his education we know little. In 1563, he matriculated at St Salvator's College, St Andrews, where he was under the special charge of the principal, Dr John Rutherford, a man, of strong character. His stay at St Andrews, however, was short, and he did not graduate. It is not certain, though it is, I think, highly probable that he spent some years on the Continent; in any case he was back in Scotland in 1571, when he is found to be domiciled at Gartness, in the parish of Drymen, Stirlingshire, where his father possessed lands. In the religious conflicts of the time he took a keen interest but, while fervent in spirit, he was also diligent in business and he handed down a very fine inheritance to his son Archibald, the first Lord Napier. He died on the 4th of April 1617, and was buried, it is fairly certain, in the old church of the parish of St Cuthbert's, Edinburgh - the church in which he was an elder.
It is very unfortunate that we know so little of the training Napier had in mathematics and we are reduced to such indications as can be gathered from his published works. In the Descriptio (p. 34) he mentions Regiomontanus, Copernicus, Lansbergius, Pitiscus and others in the Rabdologia (page 21, Lib. I., Cap. iv), he quotes the Decimal Arithmetic of "that most learned mathematician Simon Stevin," and I think it is reasonable to assume that a man of his wealth and keen interest in mathematics would possess and study carefully all the more important of the accessible publications of the time. But while his recorded work is, of course, not independent of that of his predecessors his genius enabled him to strike out along new lines that opened up a new era in mathematics.
Of the Rabdologia (Edinburgh: Andrew Hart, 1617) and the De Arte Logistica, which only appeared in 1839, I shall say nothing except that in the former the construction and use of the "numbering rods," usually called "Napier's Bones," are fully described. The "Bones" are no doubt ingenious and were extensively used for some years after his death but they are rather an ingenious toy than an arithmetical machine. The books on which Napier's fame depends are the two that expound his logarithms, namely:-
The definition of a logarithm is very different from that now so familiar. In the first place Napier speaks always of the logarithm of a sine, not of a number; it was the simplification of Trigonometric calculations he had primarily in view and therefore it was the sine that bulked most largely. It is to be remembered that in his day, and for long after, the sine was a line, not a ratio, and the whole sine meant the radius of the circle whose half-chords were the sines. In the second place he makes use of two moving points to define a logarithm.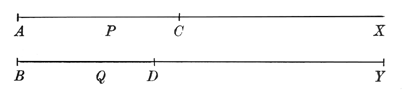
Suppose one point to set out from the point and to move along the line (of unlimited length) with a uniform velocity ; then suppose a second point to set out from on the line , of fixed length , at the same time as sets out from , starting with the velocity and moving not uniformly but so that its velocity at any point, as , is proportional to the distance from to the end of the line . If is the point has reached, moving with velocity , when , moving in the way described, has reached then the number which measures is the logarithm of the sine (or number) which measures . [In the Constructio the name "Artificial Number" is used instead of "logarithm."]
In Napier's terminology , the length of , is the whole sine; when is at is at so that the logarithm of the whole sine is . The logarithms of numbers less than are positive ("abundant"); if were to the left of then would be to the left of so that the logarithms of numbers greater than the whole sine are negative ("defective"). In the Constructio = 107 so that log 107 = 0 and as , as .
The fundamental rule on which all the others depend is that
It is quite obvious that the logarithm as thus defined is not so simple in actual work as the logarithm we now use. I may be allowed to refer to my article in the Memorial Volume for a fuller illustration of the various methods of operation.
Cumbrous as these logarithms are in many ways the Descriptio was hailed as a great discovery. Among those who recognised its merits, Henry Briggs, Professor at Gresham College, London, must be specially named. He contributed a Preface to Wright's translation, suggested that the logarithm of the tenth part of the whole sine should be a power of 10 (the logarithm of the whole sine being kept 0 as before) and began the calculation of new tables to embody his suggestion. In the summer of 1615, he journeyed to Edinburgh and stayed with Napier for a month when the proposed change was discussed. Napier, as Briggs relates, stated he was himself convinced that a change was needed and would have set about it long before had his health and leisure permitted, but he proposed a more far-reaching change than Briggs had done. He suggested namely, that zero should be the logarithm of unity, not of the whole sine, while the logarithm of the whole sine should be a power of ten. Briggs at once recognised the merit of Napier's proposal and set himself to the calculation of the new logarithms. In the following summer he again visited Napier and submitted the calculations he had made; further visits were made impossible by Napier's death and thus the calculation of logarithms in the form we now have them fell to Briggs in the first place, his Arithmetica Logarithmica appearing in 1624.
The proposal to take unity as the number whose logarithm is to be zero is vital to the ready working of logarithms and it came, as Briggs himself explicitly states, from Napier, but the credit due to Briggs for his labours in the calculation of logarithms can hardly be over-estimated; his name should always be associated with that of Napier in any fair account of the origin of logarithms.
It should be noted that what we now call Napierean logarithms are not the logarithms which Napier calculated and published in the Descriptio. The relation between the two is given by the equation.
The Descriptio (and also the Constructio) marks an important advance in theoretical Trigonometry as well as in practical calculations. For a good analysis and discussion of Napier's merits in this field I may refer to the second volume of Braunmühl's Geschichte der Trigonometrie, pp. 11-18; Professor Sommerville's article in the Memorial Volume is also well worth careful study.
"Even to-day a certain mystery surrounds the figure of the Laird of Merchiston. Appearing at the time he did, and in an environment seemingly so strangely in contrast with his special pursuits, he strikes us as the most singular of apparitions among his contemporaries. He had one fellow-countryman, indeed, as a predecessor in the study of physical science. In the thirteenth century Michael Scott, like his contemporary Roger Bacon, had given his attention to that study; had gained a continental reputation as wide as Napier's, and an equally evil name among his countrymen of being in league with the infernal powers. But between Michael and Napier we can name no Scot whose interest lay specially in the domain of science, and the explanation is simple. In Scotland, as in other countries, the universities were the exclusive centres of intellectual activity, and the studies at the Universities were under the sole dominion of the Church, which naturally laid its ban on investigations that might imperil its own teaching. By his isolation Napier is thus wrapped in a certain mystery, and the mystery is deepened by the fact that we know so little of him, and that what we do know is at times strangely incongruous with the main preoccupations of his life" (Mem. Vol., p. 34).
John Napier was born in 1550 at Merchiston Castle, near Edinburgh. Of his education we know little. In 1563, he matriculated at St Salvator's College, St Andrews, where he was under the special charge of the principal, Dr John Rutherford, a man, of strong character. His stay at St Andrews, however, was short, and he did not graduate. It is not certain, though it is, I think, highly probable that he spent some years on the Continent; in any case he was back in Scotland in 1571, when he is found to be domiciled at Gartness, in the parish of Drymen, Stirlingshire, where his father possessed lands. In the religious conflicts of the time he took a keen interest but, while fervent in spirit, he was also diligent in business and he handed down a very fine inheritance to his son Archibald, the first Lord Napier. He died on the 4th of April 1617, and was buried, it is fairly certain, in the old church of the parish of St Cuthbert's, Edinburgh - the church in which he was an elder.
It is very unfortunate that we know so little of the training Napier had in mathematics and we are reduced to such indications as can be gathered from his published works. In the Descriptio (p. 34) he mentions Regiomontanus, Copernicus, Lansbergius, Pitiscus and others in the Rabdologia (page 21, Lib. I., Cap. iv), he quotes the Decimal Arithmetic of "that most learned mathematician Simon Stevin," and I think it is reasonable to assume that a man of his wealth and keen interest in mathematics would possess and study carefully all the more important of the accessible publications of the time. But while his recorded work is, of course, not independent of that of his predecessors his genius enabled him to strike out along new lines that opened up a new era in mathematics.
Of the Rabdologia (Edinburgh: Andrew Hart, 1617) and the De Arte Logistica, which only appeared in 1839, I shall say nothing except that in the former the construction and use of the "numbering rods," usually called "Napier's Bones," are fully described. The "Bones" are no doubt ingenious and were extensively used for some years after his death but they are rather an ingenious toy than an arithmetical machine. The books on which Napier's fame depends are the two that expound his logarithms, namely:-
1. Mirifici Logarithmorum Canonis Descriptio. (Edinburgh: Andrew Hart, 1614). An English translation by Edward Wright was published in 1616, after the translator's death, by his son Samuel Wright.
2. Mirifici Logarithmorum Canonis Constructio. (Edinburgh; Andrew Hart, 1619). This work, though written several years before the Descriptio, only appeared after Napier's death and contained Notes by Briggs.
The Descriptio defines a logarithm, lays down the rules for working with logarithms, illustrating their use particularly by applying them to the solution of triangles, and contains a Table of the logarithms. The book also has an excellent discussion of theorems in Spherical Trigonometry, usually known as Napier's Rules of Circular Parts - though this is a very inadequate statement of the contribution to Trigonometry that the relative pages of the Descriptio make.
2. Mirifici Logarithmorum Canonis Constructio. (Edinburgh; Andrew Hart, 1619). This work, though written several years before the Descriptio, only appeared after Napier's death and contained Notes by Briggs.
The definition of a logarithm is very different from that now so familiar. In the first place Napier speaks always of the logarithm of a sine, not of a number; it was the simplification of Trigonometric calculations he had primarily in view and therefore it was the sine that bulked most largely. It is to be remembered that in his day, and for long after, the sine was a line, not a ratio, and the whole sine meant the radius of the circle whose half-chords were the sines. In the second place he makes use of two moving points to define a logarithm.

Suppose one point to set out from the point and to move along the line (of unlimited length) with a uniform velocity ; then suppose a second point to set out from on the line , of fixed length , at the same time as sets out from , starting with the velocity and moving not uniformly but so that its velocity at any point, as , is proportional to the distance from to the end of the line . If is the point has reached, moving with velocity , when , moving in the way described, has reached then the number which measures is the logarithm of the sine (or number) which measures . [In the Constructio the name "Artificial Number" is used instead of "logarithm."]
In Napier's terminology , the length of , is the whole sine; when is at is at so that the logarithm of the whole sine is . The logarithms of numbers less than are positive ("abundant"); if were to the left of then would be to the left of so that the logarithms of numbers greater than the whole sine are negative ("defective"). In the Constructio = 107 so that log 107 = 0 and as , as .
The fundamental rule on which all the others depend is that
if then .
In the use of logarithms as they were first defined the greatest defect is that log 1 is not zero, so that we cannot say that
.
We first write the proportion, say then or . Of course we might use instead of 1; thus let so that
Then, when x has been found, multiply by , which is easy if .
It is quite obvious that the logarithm as thus defined is not so simple in actual work as the logarithm we now use. I may be allowed to refer to my article in the Memorial Volume for a fuller illustration of the various methods of operation.
Cumbrous as these logarithms are in many ways the Descriptio was hailed as a great discovery. Among those who recognised its merits, Henry Briggs, Professor at Gresham College, London, must be specially named. He contributed a Preface to Wright's translation, suggested that the logarithm of the tenth part of the whole sine should be a power of 10 (the logarithm of the whole sine being kept 0 as before) and began the calculation of new tables to embody his suggestion. In the summer of 1615, he journeyed to Edinburgh and stayed with Napier for a month when the proposed change was discussed. Napier, as Briggs relates, stated he was himself convinced that a change was needed and would have set about it long before had his health and leisure permitted, but he proposed a more far-reaching change than Briggs had done. He suggested namely, that zero should be the logarithm of unity, not of the whole sine, while the logarithm of the whole sine should be a power of ten. Briggs at once recognised the merit of Napier's proposal and set himself to the calculation of the new logarithms. In the following summer he again visited Napier and submitted the calculations he had made; further visits were made impossible by Napier's death and thus the calculation of logarithms in the form we now have them fell to Briggs in the first place, his Arithmetica Logarithmica appearing in 1624.
The proposal to take unity as the number whose logarithm is to be zero is vital to the ready working of logarithms and it came, as Briggs himself explicitly states, from Napier, but the credit due to Briggs for his labours in the calculation of logarithms can hardly be over-estimated; his name should always be associated with that of Napier in any fair account of the origin of logarithms.
It should be noted that what we now call Napierean logarithms are not the logarithms which Napier calculated and published in the Descriptio. The relation between the two is given by the equation.
Napier's logarithm of where and is our Napierian logarithm of .
Napier's method of calculating his logarithms is given in the Constructio, but into that subject I cannot enter.
The Descriptio (and also the Constructio) marks an important advance in theoretical Trigonometry as well as in practical calculations. For a good analysis and discussion of Napier's merits in this field I may refer to the second volume of Braunmühl's Geschichte der Trigonometrie, pp. 11-18; Professor Sommerville's article in the Memorial Volume is also well worth careful study.
Last Updated April 2007