Gibson History 5 - James Gregory
In the 16th century great progress was being made in the development of algebra and in the 17th the progress was still more rapid. Though Scotsmen on the Continent, such as Alexander Anderson, who had settled in Paris, were active workers, Napier had no distinguished successor in Scotland until the second half of the 17th century, when we find the names of two men who made substantial contributions to pure and applied mathematics, James Gregory and his nephew David.
James Gregory (born 1638) was the third son of the Rev. John Gregory, minister of Drumoak, a small parish near Aberdeen. His mother was the daughter of David Anderson of Finzeach in Aberdeenshire, and related to the Alexander Anderson, just mentioned as a teacher in Paris. Gregory is said to have received his first lessons in mathematics from his mother, but in due course he passed on, first to the Grammar School and then to Marischal College, Aberdeen, where he graduated. In 1663 his Optica Promota was published in London and he spent some time in that city after the publication of his book in the hope of securing facilities for constructing a telescope on the principles he had laid down in the Optica. His efforts were, however, unsuccessful and he went to Italy where he continued his mathematical studies. After a residence of about three years in Padua he returned, in 1668, to Scotland. In 1669 he was appointed to the Chair of Mathematics at St Andrews; in that position be had a busy and, as the years passed, a rather troubled life so that he was glad to accept a call in 1674 to be Professor of Mathematics at Edinburgh where, as he says in a letter to a friend in Paris, "my salary is double and my encouragements much greater." (Acad. Greg. p. 49). His Edinburgh professorship was, however, very brief as he died in October 1675.
The mathematical writings of Gregory that were published under his own supervision, in addition to the Optica Promota, are :-
The Quadratura and the Geometriae Pars Universalis are not altogether easy to read but the difficulty is due not so much to any obscurity in the reasoning as to the cumbrous phraseology of the geometrical form in which the demonstrations are carried out. If the books were re-written and the symbolism of modern mathematics employed throughout very much of the difficulty would disappear.
Quadratura. If is a sector of a circle (or ellipse or hyperbola), being the centre and the tangents at and let the triangle be called an inscribed triangle and the quadrilateral a circumscribed quadrilateral.
Let be the tangent to the arc at where cuts it; then the quadrilateral is a second inscribed quadrilateral and the polygon a second circumscribed figure.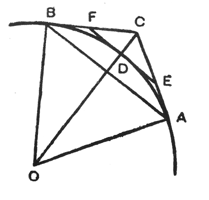
Proceeding in this way Gregory constructs pairs of inscribed and circumscribed figures, thus forming two sets (S)
In the course of the work Gregory shows great skill in carrying through complicated calculations in spite of very inadequate symbolism but the main interest now-a-days does not lie in the calculations. The important point is that he seeks to prove that , the termination of the converging series, can not be an algebraic function of any pair of the terms . To find the termination he says we must find a function such that and then if is the termination . Here are any pair, i.e. are variables and if such a function can be found it will give . Now Gregory tries to prove, and believes he does prove, that is not an algebraic function and that therefore circular (and also logarithmic) functions are not algebraic. His method of defining the degree of his algebraic function is not at all clear or satisfactory and would need fuller development, but, whatever decision we come to on that matter, it is a very remarkable attempt and is a striking proof of Gregory's philosophic acumen. His work applies to the hyperbola as well as to the circle so that logarithms come within its scope.
Geometriae Pars Universalis. - The aim of the Geometriae Pars Universalis is wider. It may be briefly described as an attempt to reduce to a coherent system the various methods ' that had been applied in the investigation of the rectification and quadrature of curves, the cubature of solids, the determination of centres of gravity and problems of maxima and, minima. He says that in the more obvious propositions he uses the methods of Cavalieri, but that his chief object is to establish his propositions with geometric rigour. He shows wide reading but the methods adopted in the principal propositions seem to me to indicate a specially close affinity with Fermat's work of which he might have obtained a knowledge through Herigone's Supplementum Cursus Mathematici (vol. 6 of the Cursus) which was published in 1644.
The subtangent is an essential element in his work and in the 7th Proposition he shows how to find it or (what is the same thing) how to find for "those curves which Descartes calls geometrical." He works out the gradient for the curve
His fundamental theorem in quadrature is, curiously enough, that which determines the surface of that part of a cylinder of height with generators perpendicular to the -plane and the are of the curve between the points for which has the values and as guiding curve. In modern symbols, if represents the arc, the surface is
Again if and are the end-points of the graph of he establishes the theorem
In a series of propositions he discusses the mensuration of the surface of paraboloids and hyperboloids of revolution and of spheroids and rectifies parabolic arcs. He works out in detail the rectification of the curve for the case and states that his method applies for every positive integral value of ,; the proof was, I think, well within his competence.
Gregory's developments in the Geometria and the Exercitationes show plainly that what we now call the Differential and Integral Calculus was near at hand, but while the great range of results and the ingenuity of the demonstrations are worthy of recognition the vital connection between differentiation and integration is not yet stated as is necessary for the advance that followed from Barrow's developments (Lect. Geom., X, x.)
Gregory's name is usually attached to a series for and except in this connection and in relation to the phrase "convergent series" it is rarely mentioned. But the source from which the series issued sent forth many more theorems of great importance which seem to have been unnoticed. I may refer to my paper in the Proc. Edinb. Math. Soc. for an account of these phases of Gregory's work. I would like, however, to emphasise the fact - for I think it is a fact - that the assertion, so often repeated in the Commercium Epistolicum, of Gregory's indebtedness to Newton is simply not true; it is very little to the credit of the compilers of that volume that they misrepresented and deliberately concealed the great number of quite independent results that Gregory had attained. From the paper referred to it will be seen that Gregory had worked out for himself
James Gregory (born 1638) was the third son of the Rev. John Gregory, minister of Drumoak, a small parish near Aberdeen. His mother was the daughter of David Anderson of Finzeach in Aberdeenshire, and related to the Alexander Anderson, just mentioned as a teacher in Paris. Gregory is said to have received his first lessons in mathematics from his mother, but in due course he passed on, first to the Grammar School and then to Marischal College, Aberdeen, where he graduated. In 1663 his Optica Promota was published in London and he spent some time in that city after the publication of his book in the hope of securing facilities for constructing a telescope on the principles he had laid down in the Optica. His efforts were, however, unsuccessful and he went to Italy where he continued his mathematical studies. After a residence of about three years in Padua he returned, in 1668, to Scotland. In 1669 he was appointed to the Chair of Mathematics at St Andrews; in that position be had a busy and, as the years passed, a rather troubled life so that he was glad to accept a call in 1674 to be Professor of Mathematics at Edinburgh where, as he says in a letter to a friend in Paris, "my salary is double and my encouragements much greater." (Acad. Greg. p. 49). His Edinburgh professorship was, however, very brief as he died in October 1675.
The mathematical writings of Gregory that were published under his own supervision, in addition to the Optica Promota, are :-
1. Vera Circuli et Hyperbolae Quadratura in propria sua proportionis specie inventa et demonstrata: Patavii, 1667.
2. A reprint of the Quadratura with an important addition, Geometriae Pars Universalis, inserviens quantitatum curvarum transmutationi et mensurae: Patavii, 1668.
3. Exercitationes Geometricae: London, 1668.
Much of Gregory's most original work is to be found in Rigaud's Correspondence of Scientific Men of the Seventeenth Century; had his letters been published as they were received he would have taken a much larger place in mathematical history than has usually been assigned him. (For an account of these letters see Proc. Edin. Math. Soc., vol 41.)
2. A reprint of the Quadratura with an important addition, Geometriae Pars Universalis, inserviens quantitatum curvarum transmutationi et mensurae: Patavii, 1668.
3. Exercitationes Geometricae: London, 1668.
The Quadratura and the Geometriae Pars Universalis are not altogether easy to read but the difficulty is due not so much to any obscurity in the reasoning as to the cumbrous phraseology of the geometrical form in which the demonstrations are carried out. If the books were re-written and the symbolism of modern mathematics employed throughout very much of the difficulty would disappear.
Quadratura. If is a sector of a circle (or ellipse or hyperbola), being the centre and the tangents at and let the triangle be called an inscribed triangle and the quadrilateral a circumscribed quadrilateral.
Let be the tangent to the arc at where cuts it; then the quadrilateral is a second inscribed quadrilateral and the polygon a second circumscribed figure.

Proceeding in this way Gregory constructs pairs of inscribed and circumscribed figures, thus forming two sets (S)
inscribed polygons
circumscribed polygons.
For the circle form an increasing sequence, a decreasing sequence and these are connected by the relations
circumscribed polygons.
,
,
lim (lim as ).
The two sequences (S) are called a "converging series," the corresponding pairs are called "converging terms," and the common limit is called "the termination of the series." It is from this beginning that the term "convergence" comes into use in connection with series.
,
lim (lim as ).
In the course of the work Gregory shows great skill in carrying through complicated calculations in spite of very inadequate symbolism but the main interest now-a-days does not lie in the calculations. The important point is that he seeks to prove that , the termination of the converging series, can not be an algebraic function of any pair of the terms . To find the termination he says we must find a function such that and then if is the termination . Here are any pair, i.e. are variables and if such a function can be found it will give . Now Gregory tries to prove, and believes he does prove, that is not an algebraic function and that therefore circular (and also logarithmic) functions are not algebraic. His method of defining the degree of his algebraic function is not at all clear or satisfactory and would need fuller development, but, whatever decision we come to on that matter, it is a very remarkable attempt and is a striking proof of Gregory's philosophic acumen. His work applies to the hyperbola as well as to the circle so that logarithms come within its scope.
Geometriae Pars Universalis. - The aim of the Geometriae Pars Universalis is wider. It may be briefly described as an attempt to reduce to a coherent system the various methods ' that had been applied in the investigation of the rectification and quadrature of curves, the cubature of solids, the determination of centres of gravity and problems of maxima and, minima. He says that in the more obvious propositions he uses the methods of Cavalieri, but that his chief object is to establish his propositions with geometric rigour. He shows wide reading but the methods adopted in the principal propositions seem to me to indicate a specially close affinity with Fermat's work of which he might have obtained a knowledge through Herigone's Supplementum Cursus Mathematici (vol. 6 of the Cursus) which was published in 1644.
The subtangent is an essential element in his work and in the 7th Proposition he shows how to find it or (what is the same thing) how to find for "those curves which Descartes calls geometrical." He works out the gradient for the curve
but lays down no general rule; each particular case is simply stated when required and a reference is given to this Proposition for the method of determining it. So far as algebraic curves are concerned he evidently was master of but his lack of algebraic symbolism makes itself painfully felt in all these investigations.
His fundamental theorem in quadrature is, curiously enough, that which determines the surface of that part of a cylinder of height with generators perpendicular to the -plane and the are of the curve between the points for which has the values and as guiding curve. In modern symbols, if represents the arc, the surface is
(both integrals are from to ).
His proof is extremely careful; the curve is expressly stated to be such that f(x) is either monotonic or made up of a finite number of monotonic parts. If h is taken as unity the integral gives the length of the are; but he extends the proposition to various cases in which is a function of and also to cases in which is taken as the variable of integration. In this way he is able to effect many integrations that do not seem to us to come naturally within his scope. For example he finds (in the Exercitationes) the integrals of and ; he also uses, as if it were quite familiar the integral of , which is very easily established by his methods.
Again if and are the end-points of the graph of he establishes the theorem
(the first integral is from to , the second to )
and applies it to give a beautiful proof of the quadrature of .
In a series of propositions he discusses the mensuration of the surface of paraboloids and hyperboloids of revolution and of spheroids and rectifies parabolic arcs. He works out in detail the rectification of the curve for the case and states that his method applies for every positive integral value of ,; the proof was, I think, well within his competence.
Gregory's developments in the Geometria and the Exercitationes show plainly that what we now call the Differential and Integral Calculus was near at hand, but while the great range of results and the ingenuity of the demonstrations are worthy of recognition the vital connection between differentiation and integration is not yet stated as is necessary for the advance that followed from Barrow's developments (Lect. Geom., X, x.)
Gregory's name is usually attached to a series for and except in this connection and in relation to the phrase "convergent series" it is rarely mentioned. But the source from which the series issued sent forth many more theorems of great importance which seem to have been unnoticed. I may refer to my paper in the Proc. Edinb. Math. Soc. for an account of these phases of Gregory's work. I would like, however, to emphasise the fact - for I think it is a fact - that the assertion, so often repeated in the Commercium Epistolicum, of Gregory's indebtedness to Newton is simply not true; it is very little to the credit of the compilers of that volume that they misrepresented and deliberately concealed the great number of quite independent results that Gregory had attained. From the paper referred to it will be seen that Gregory had worked out for himself
(i) The Binomial Theorem in its most general form;
(ii) the general expression for in terms of and of the finite differences ... and
(iii) general series for the sines and cosines of multiple angles, with a large variety of series for the mensuration of the circle.
Later, after seeing one of Newton's series, he developed many series and for the inspiration, though not for the methods, he was in these cases indebted, I think, to the simple statement (without explanations of any kind) of the Newtonian series.
(ii) the general expression for in terms of and of the finite differences ... and
(iii) general series for the sines and cosines of multiple angles, with a large variety of series for the mensuration of the circle.
Last Updated April 2007