The development of the 'black hole' concept
Black holes as we understand them today have faced a lot of opposition since the conception of the idea, even from those who worked extensively on them. Initially based solely in the workings of mathematics and the imagination, they have since become a widely celebrated and heavily studied, serious area of science.
NASA defines a black hole to be [32]:-
The publication of Isaac Newton's Philosophiae Naturalis Principia Mathematica in 1687 set out his ideas on the notion of gravity, outlining his law of universal gravitation. This law states that every body attracts every other body by a force acting along the line connecting their centres of gravity. This force is directly proportional to the product of the two masses, and inversely proportional to the square of the distance separating their centres of gravity.
Written mathematically, this law states
With his understanding of the fundamentals of gravity, John Michell (1724-1793), having previously studied twin stars, in 1784 went on to propose the idea that there could exist a body sufficiently massive that even light could not escape. Let us note as an aside that he had argued twin stars were physically close using a statistical argument, saying that that the odds against this not being the case were many million millions to one. He appears to have been the first to use statistical arguments in astronomy.
At the time it was understood, largely because of Newton's promotion of the idea, that light consisted of particles (or corpuscles) that were projected from a source, and thus acted like any other projectile, i.e. could vary in speed. Therefore, it was believed that gravity could act on light accordingly, and, if a body was massive enough, its gravitational pull could prevent light from leaving a star to reach an observer's eye.
It was Michell who first suggested the existence of such a physical body in his letter to Henry Cavendish, published in November 1784 in the Philosophical Transactions of the Royal Society of London. Michell referred to these objects as 'dark stars' (see [31]). Earlier in the 18th century, English astronomer James Bradley had given a value for the speed of light: he had calculated that it travelled at 301,000,000 m/s (rather close to today's c = 299,792,458 m/s). Michell considered the reduction of the speed of the light particles from a given star in order to calculate its mass. He understood the concept of escape velocity (minimum velocity required to escape from a body's gravitational pull), thus questioned how massive a star would have to be for its escape velocity to be greater than the speed of light.
Michell's simplistic calculations assumed that the density of a 'dark star' would be the same as that of the Sun, and concluded that such a body could form if the diameter of a star was greater than 500 times that of the Sun making the escape velocity at the surface greater than the speed of light. Michell also noted that in order to detect these non-radiating bodies, one would have to observe the gravitational effects on nearby bodies. Here he used his twin stars work, arguing that a dark star and a bright star in orbit around each other would be detectable by the periodic movement of the bright star.
However, at the time, it was not known that light travelled at a constant speed, as would be postulated by Einstein later. Thus the erroneous thought of light slowing down and falling back to the star's surface was not faced with objection. The notion of a black hole did not really take off either; black holes were yet to enter their phase of popularity, and Michell's work went unnoticed until it resurfaced in the 1970s.
Furthermore, with the growing approval of light's wave-like nature, initiated by Robert Hooke and Christiaan Huygens in the late 17th century and developed by Thomas Young in the early 19th century, it was unclear how gravity could influence light if it were a wave rather than a particle. Michell's idea was unlikely to be rediscovered with the advance in belief in light-waves.
Another mathematical 'proof' was however offered independently of Michell by Pierre-Simon Laplace in 1799 in favour of what Michell had proposed, but with different conclusions on the ratios of density and size. Like Michell, Laplace was working with the assumption that light was formed of particles behaving like projectiles. Moreover, his proof was only provided after the insistence of German astronomer Franz Xaver von Zach (1754-1832), who demanded more than the brief quantitative reasoning that was given in Laplace's original 1796 paper Exposition du Système du Monde. There is even some debate as to whether or not Laplace even believed in black holes. In subsequent editions of Système du Monde, he removed his 'invisible-star' theory, and never mentioned it again. Perhaps he lost interest, or perhaps he too accepted the light-as-a-wave theory, thus dispelling his notion of a black hole.
Both Laplace and Michell were working with inadequate laws of light. They were also both wrong in their predictions of what stellar black holes were like [26]:-
Little new was offered for the next century that would further the development of the concept of the black hole, and it would take some revolutionary thinking to restart its progression.
Albert Einstein's Theory of General Relativity, published 1915, regarded space and time as a curved four-dimensional object. In fact it had been noted by Hermann Minkowski in 1907 that Einstein's Special Theory of Relativity published in 1905 meant that time was just another dimension. No longer should space and time be considered absolute, but relative depending upon the observer's frame of reference. He argued this by postulating a constant velocity of light, regardless of an observer's frame of reference.
A constant velocity of light implies a relative time and space: suppose person A was on a train travelling 100 km/h and they threw a ball vertically upward, and caught it. In their frame of reference (on the train), the ball appears to have no horizontal velocity, i.e. it travels at 0 km/h horizontally. Let person B not be on the train, rather, beside the track. Suppose they can see the ball and observe its motion. Then from their frame of reference, the ball appears to move at 100 km/h.
The difference between a ball and light, is that Einstein said light would always, no matter what frame of reference the observers were in, always be measured with the same velocity, c. With the train analogy, the difference in measured velocities of the ball from the two frames of reference is 100 km/h, however, with light, there can be no difference in measurement, even if it were measured from a frame of reference travelling at almost the speed of light. Therefore, since velocity equals distance divided by time, if velocity is constant, distance and time must vary depending upon the frame of reference. In other words, distance and time are relative.
Rather than a force, Einstein viewed gravity as a warping of time and space. General relativity says that massive bodies bend the space around them, causing objects to deviate from the straight line path they would have travelled in undistorted space-time. This is often depicted as a mass sitting on a rubber sheet, thus stretching the centre downwards. The greater the mass, the further down the rubber sheet is depressed. With a black hole, a sort of sink is formed on this rubber sheet due to the black hole's immense mass.
However, like many before, and many after, who worked on the physics behind black holes, Laplace and Hawking included, Einstein doubted the existence of such a physical body being possible, due to the requirement of the physical existence of a singularity. While his formulae allowed for their existence, he did not believe that nature would. This was not uncommon at the time and to give the actual existence of black holes much serious consideration was dangerous for a scientist's career.
Einstein presented his general relativity with ten field equations that describe the impact of gravity in a curved space-time. While addressing the issue of Mercury's shifting perihelion, he was only able to give an approximate solution to his equations. It may then have come as a pleasant surprise to Einstein when only a month after the publication of his theory, he received a letter from German physicist Karl Schwarzschild with his exact solution to the field equations. Einstein wrote back in 1916 [20]:-
Schwarzschild believed that the outward pressure exerted as matter was squeezed into a singularity would be sufficient to prevent a black hole actually forming. He reported that this problem of the formation of a black hole [1]:-
The debate over black holes' existence flared up between Indian American astrophysicist, then student of Cambridge University, Subrahmanyan Chandrasekhar, and English astronomer Arthur Eddington in the 1930s. Having seemingly befriended Chandrasekhar and encouraged his work at Cambridge, Eddington orchestrated a damning attack on the young astrophysicist's labours.
In 1930, on a voyage from India to England, Chandrasekhar had calculated that a white dwarf much heavier than the Sun could not exist, and that it would undergo a collapse into a singularity with infinite density. On 11 January 1935, with Eddington's apparent approval, Chandrasekhar was to deliver his results to a meeting of the Royal Astronomical Society in London. Little did he know, Eddington had prepared his own talk, and would give it directly following Chandrasekhar's.
Eddington belittled Chandrasekhar's argument, declaring that due to its solely mathematical basis, it had no bearing on the physical universe. How could something so large as a star effectively disappear? He upheld the view that white dwarfs could not totally collapse. Though Eddington's case was fairly unsubstantiated, the Briton's reputation prevented anyone from daring to openly disagree with him. Even Chandrasekhar was not given the chance to respond to Eddington's retort.
More information on the Chandrasekhar and Eddington dispute is given at THIS LINK.
Their rivalry on the matter continued for some years. At a meeting in Paris in 1939, Eddington maintained his disapproval of Chandrasekhar's ideas, despite the quiet, growing support for Chandrasekhar from the likes of Niels Bohr, Wolfgang Pauli and Paul Dirac. By this stage, it was widely believed that Eddington misunderstood the problem, thus he became largely ignored on this topic. At the meeting, Eddington claimed that there was no experimental test that could determine which of the two notions was correct. This was a valid point, but astronomer and white dwarf expert Gerard Kuiper was on hand to immediately refer to his work supporting Chandrasekhar. Eddington reluctantly apologised for hurting Chandrasekhar, but still refused to bow to his theory. Eddington's reluctance to accept what Chandrasekhar put forward supposedly had racial and sexually-repressive undertones, as well as stemming from the fact that acceptance of Chandrasekhar's argument would totally discredit what Eddington had been claiming for many years. No doubt an element of pride was present.
This condemnation of Chandrasekhar's suggestions by such an esteemed figure as Eddington possibly delayed the development of the black hole concept by decades. No-one followed up the claims made by Chandrasekhar, and the Indian himself turned to other fields, leaving Cambridge, where he felt his life and career had been harassed by racism, for Chicago. However, Canadian physicist Werner Israel, who studied in depth the scientific temper of these times, rejects this, claiming that Eddington's support would have made little difference to the sway of public opinion of Chandrasekhar's theory. Regardless, it would not be until 1983 that Chandrasekhar would be awarded the Nobel Prize for his work on white dwarfs.
Black holes had not even received their universal title until the 1960s. Previously known as 'darks stars', 'collapsars' and 'gravitationally completely collapsed objects' to name a few terms, the expression 'black hole' is popularly attributed to physicist John Wheeler, who admitted the term was offered to him by an audience member of one of his lectures in 1967. The use of the words 'black hole' had previously been used in 1963 at an astrophysics conference in Dallas, as claimed by science writer Marcia Bartusiak in [1]. Wheeler perhaps was merely the first with the scientific authority to use the phrase, hence its popularity took off and credit is often given to him. Just based on Google's Ngram viewer it can be seen that the use of the words 'black hole' in publications increased dramatically in and after the 1960s.
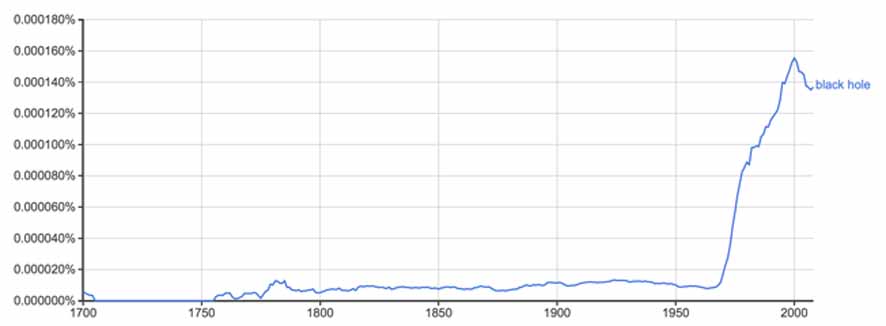
Chandrasekhar never opted to speculate what would happen to a star of sufficient mass, i.e. exceeding what would become known as the Chandrasekhar limit. This did not stop others from doing so however. Within two years of the discovery of the neutron by James Chadwick in 1932, German and Swiss astronomers, respectively Walter Baade and Fritz Zwicky, proposed the existence of neutron stars at a meeting of the American Physical Society. Whilst studying the cause of supernovae, they concluded that during such explosions, ordinary stars are turned into stars consisting of extremely closely packed neutrons, hence their name neutron star. A supernova can occur when a white dwarf in a binary star system essentially steals matter from its partner, gaining too much mass. Its core temperature rises enough to cause runaway nuclear fusion. Similar conclusions on neutron stars had also been made by Russian scientist Lev Davidovich Landau in 1931 before neutrons were discovered. He had also calculated that a star which was heavy enough could collapse to a point, but thinking this was ridiculous, he proposed that it would end up as a "one immense nucleus."
What's important is that at the time, a neutron star would be the densest object in the universe. While their existence was treated with the same hesitation as that of black holes, their observation would certainly help sway opinion over the possibility of the physical existence of black holes.
Moreover, just as Chandrasekhar had predicted an upper limit for white dwarfs, 1939 saw a paper in Physical Review by American theoretical physicist J Robert Oppenheimer and his graduate student at University of California, Berkley, George Volkoff, in which they predicted an equivalent constraint on neutron stars. They did not however know what would occur if a neutron star's mass exceeded this limit.
Following up this research, this time with a different graduate student, Hartland Snyder, Oppenheimer determined that if a star's core was more massive than two or three solar masses, then the stellar remnant would neither become a white dwarf nor a neutron star but would undergo "continued gravitational contraction." They calculated that mathematics predicted the such a star would continue to contract indefinitely leading to a singularity, the stuff of nightmares for physicists.
Though in this publication Oppenheimer and Snyder had offered the first modern description of black holes, the paper came out on 1 September 1939, the day of Germany's invasion of Poland triggering the start of the Second World War, and thus received little attention.
At this time, very few astronomers were ready to believe that such strange objects could exist in the real world. Even Einstein attempted to prove the impossibility of their existence in his paper published in 1939, only a month after Oppenheimer and Snyder's. However, Einstein had not even read Oppenheimer-Snyder, and his paper was considered as one of his worst. Stuck with the past's way of thinking, and with the teaching of relativity confined to mathematics rather than physics departments (or banned completely as happened during the Third Reich), most astronomers almost did not want such objects to be possible. It certainly helped their cause that there had yet to be any observations of neutron stars, let alone black holes.
Thus the work of British astronomer Jocelyn Bell can be considered important in the black hole concept's development. In 1967, she, along with radio astronomer Antony Hewish, picked up radio pulses from an unknown source. Initially dubbed LGM-1 (for "Little Green Men 1", since they considered the source could be an extraterrestrial civilisation), it was later found to be a rapidly rotating neutron star - the first observational evidence that neutron stars existed. Most of the known neutron stars have been found by detecting their regularly emitted radio pulses.
It was around this time that the tide was turning toward general acceptance of the possible existence of bodies such as black holes. Again using Google's Ngram viewer, when compared to other names used before 'black hole' was popularised, it can be inferred that worldwide acceptance of the concept of a black hole really only took off after the 1960s, since that was the first time any of the terms used for the concept became frequently used in publications.
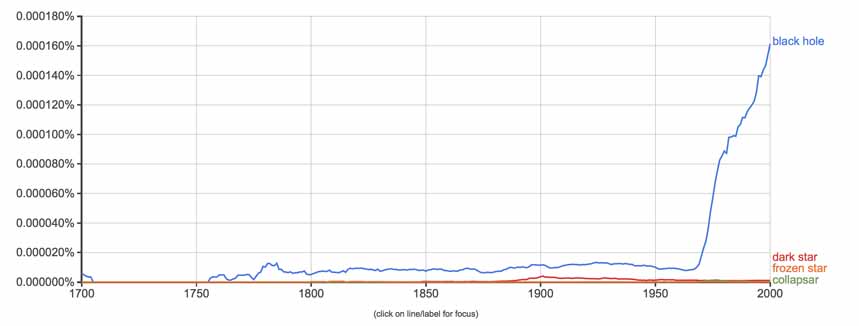
More and more time was put into the study of black holes, including those of British theoretical physicist Stephen Hawking. By the end of the 1960s, both Werner Israel and British mathematician Roger Penrose with John Wheeler had helped revolutionise the study of black holes.
Israel, using general relativity, showed that non-rotating black holes had to be very simple; they were perfectly spherical, their size depended upon their mass only, and any two such black holes with the same mass must be identical. He, and many others, believed that the only way a black hole, which had to be perfectly spherical, could form was if it was created from the collapse of a perfectly spherical object. Thus any real star, which would never be perfectly spherical, would only ever collapse to form a naked singularity.
Penrose and Wheeler however argued that due to the rapid movements involved in a star's collapse, the gravitational waves given off would make it ever more and more spherical until it settled to a stationary state, where it would be perfectly spherical.
In 1970, Hawking, using quantum theory and general relativity, was able to show that black holes can actually emit radiation, giving a theoretical argument for their existence in 1974. This is the prediction for what is now know as Hawking Radiation. By radiating, black holes conserve entropy, solving the incompatibility problem with the second law of thermodynamics. This added to the argument for their physical existence.
According to quantum physics, particle-antiparticle pairs are constantly being produced throughout the universe. What happens in nearly every case is that they almost instantly annihilate with each other, releasing energy into the universe. Hawking postulated that were such a particle pair to form near a black hole's event horizon, then before given the chance to annihilate, one of the pair could be dragged toward the black hole's singularity, while the other escapes. It is in this form that black holes are said to radiate. This challenges what general relativity says about nothing being able to escape from the clutches of a black hole. Moreover, Hawking stated that since a black hole radiates in such a manner, it shrinks, evaporating until it vanishes.
Naturally, as with most discoveries in this field, Hawking Radiation poses yet more unanswered questions. If a black hole shrinks, what happens to the information that was put into it? This leads to the information paradox since quantum mechanics says information cannot be deleted.
Despite all the doubt throughout the many years of work on black holes, the likelihood of their physical reality is almost certain. What is now widely accepted as the first discovered black hole, Cygnus X-1 was first 'seen' in 1964, and was generally recognised as a black hole by the 1990s. It was the subject of a bet in 1974 between Hawking and American theoretical physicist Kip Thorne, which Hawking conceded in 1990, admitting that Cygnus X-1 was indeed in all likelihood a black hole, based on the sufficient observational data they had.
Further support has been offered by the Hubble Space Telescope (HST) not just in verifying black holes' existence, but also in backing up claims made since the 1960s regarding galaxies each containing a supermassive black hole at their centre. Launched in 1990, the HST has allowed astronomers to conclude that black holes are probably common to the centres of all galaxies.
One of the latest observational discoveries in this field has come from the LIGO (Laser Interferometer Gravitational-Wave Observatory) and Virgo Scientific Collaboration. Observed on 14 September 2015, the Collaboration announced on 11 February 2016 that they had made the first observational discovery of gravitational waves (disturbances in the curvature of space-time generated by accelerated masses). They had emerged from a collision of two black holes. This offered the first observational evidence for the existence of binary black hole systems. In 2017, Kip Thorne was one of three (Thorne, Barry Barish, Rainer Weiss) to receive the Nobel Prize for contribution to the detection of gravitational waves.
It is still unclear how singularities apply in reality. This poses the question over the limit of mathematics' ability to fully model nature. Alternatively, singularities imply that we have yet to develop a complete description of the universe and its workings: it may be that some of the notions we take as firm truths are just not quite correct.
The concept of a black hole has overcome a great deal of resistance to get to the point of acceptance it enjoys today. With its conceptual development, a large number of scientists have made their name bringing what was initially just a mathematical concept, ridiculed for its lack of physical meaning, into the forefront as one of astronomy's most exciting realities, questioning long held beliefs of the workings of the universe. Resistance was futile; black holes are inescapable.
NASA defines a black hole to be [32]:-
... a region in space where the pulling force of gravity is so strong that light is not able to escape.Thus to consider the origins of the development of the black hole concept, the understanding of gravity, and also of light, must be considered.
The publication of Isaac Newton's Philosophiae Naturalis Principia Mathematica in 1687 set out his ideas on the notion of gravity, outlining his law of universal gravitation. This law states that every body attracts every other body by a force acting along the line connecting their centres of gravity. This force is directly proportional to the product of the two masses, and inversely proportional to the square of the distance separating their centres of gravity.
Written mathematically, this law states
where is the gravitational force acting between the two objects with masses and (in kilograms). The distance between the centre of gravity of each of the masses is denoted , and is the universal gravitational constant, with value around m kg s (m = metres, kg = kilograms, s = seconds).
With his understanding of the fundamentals of gravity, John Michell (1724-1793), having previously studied twin stars, in 1784 went on to propose the idea that there could exist a body sufficiently massive that even light could not escape. Let us note as an aside that he had argued twin stars were physically close using a statistical argument, saying that that the odds against this not being the case were many million millions to one. He appears to have been the first to use statistical arguments in astronomy.
At the time it was understood, largely because of Newton's promotion of the idea, that light consisted of particles (or corpuscles) that were projected from a source, and thus acted like any other projectile, i.e. could vary in speed. Therefore, it was believed that gravity could act on light accordingly, and, if a body was massive enough, its gravitational pull could prevent light from leaving a star to reach an observer's eye.
It was Michell who first suggested the existence of such a physical body in his letter to Henry Cavendish, published in November 1784 in the Philosophical Transactions of the Royal Society of London. Michell referred to these objects as 'dark stars' (see [31]). Earlier in the 18th century, English astronomer James Bradley had given a value for the speed of light: he had calculated that it travelled at 301,000,000 m/s (rather close to today's c = 299,792,458 m/s). Michell considered the reduction of the speed of the light particles from a given star in order to calculate its mass. He understood the concept of escape velocity (minimum velocity required to escape from a body's gravitational pull), thus questioned how massive a star would have to be for its escape velocity to be greater than the speed of light.
Michell's simplistic calculations assumed that the density of a 'dark star' would be the same as that of the Sun, and concluded that such a body could form if the diameter of a star was greater than 500 times that of the Sun making the escape velocity at the surface greater than the speed of light. Michell also noted that in order to detect these non-radiating bodies, one would have to observe the gravitational effects on nearby bodies. Here he used his twin stars work, arguing that a dark star and a bright star in orbit around each other would be detectable by the periodic movement of the bright star.
However, at the time, it was not known that light travelled at a constant speed, as would be postulated by Einstein later. Thus the erroneous thought of light slowing down and falling back to the star's surface was not faced with objection. The notion of a black hole did not really take off either; black holes were yet to enter their phase of popularity, and Michell's work went unnoticed until it resurfaced in the 1970s.
Furthermore, with the growing approval of light's wave-like nature, initiated by Robert Hooke and Christiaan Huygens in the late 17th century and developed by Thomas Young in the early 19th century, it was unclear how gravity could influence light if it were a wave rather than a particle. Michell's idea was unlikely to be rediscovered with the advance in belief in light-waves.
Another mathematical 'proof' was however offered independently of Michell by Pierre-Simon Laplace in 1799 in favour of what Michell had proposed, but with different conclusions on the ratios of density and size. Like Michell, Laplace was working with the assumption that light was formed of particles behaving like projectiles. Moreover, his proof was only provided after the insistence of German astronomer Franz Xaver von Zach (1754-1832), who demanded more than the brief quantitative reasoning that was given in Laplace's original 1796 paper Exposition du Système du Monde. There is even some debate as to whether or not Laplace even believed in black holes. In subsequent editions of Système du Monde, he removed his 'invisible-star' theory, and never mentioned it again. Perhaps he lost interest, or perhaps he too accepted the light-as-a-wave theory, thus dispelling his notion of a black hole.
Both Laplace and Michell were working with inadequate laws of light. They were also both wrong in their predictions of what stellar black holes were like [26]:-
They both went for the 'big star' option. But this was wrong. The black holes that have been found are all very small in size and very high in density.Modern relativity rejects Michell's notion of light emanating directly from a surface, slowing due to gravity, and then falling back again. This is because it is now understood that the speed of light remains constant in empty space, thus cannot slow down and stop in the conventional sense that a normal projectile can.
Little new was offered for the next century that would further the development of the concept of the black hole, and it would take some revolutionary thinking to restart its progression.
Albert Einstein's Theory of General Relativity, published 1915, regarded space and time as a curved four-dimensional object. In fact it had been noted by Hermann Minkowski in 1907 that Einstein's Special Theory of Relativity published in 1905 meant that time was just another dimension. No longer should space and time be considered absolute, but relative depending upon the observer's frame of reference. He argued this by postulating a constant velocity of light, regardless of an observer's frame of reference.
A constant velocity of light implies a relative time and space: suppose person A was on a train travelling 100 km/h and they threw a ball vertically upward, and caught it. In their frame of reference (on the train), the ball appears to have no horizontal velocity, i.e. it travels at 0 km/h horizontally. Let person B not be on the train, rather, beside the track. Suppose they can see the ball and observe its motion. Then from their frame of reference, the ball appears to move at 100 km/h.
The difference between a ball and light, is that Einstein said light would always, no matter what frame of reference the observers were in, always be measured with the same velocity, c. With the train analogy, the difference in measured velocities of the ball from the two frames of reference is 100 km/h, however, with light, there can be no difference in measurement, even if it were measured from a frame of reference travelling at almost the speed of light. Therefore, since velocity equals distance divided by time, if velocity is constant, distance and time must vary depending upon the frame of reference. In other words, distance and time are relative.
Rather than a force, Einstein viewed gravity as a warping of time and space. General relativity says that massive bodies bend the space around them, causing objects to deviate from the straight line path they would have travelled in undistorted space-time. This is often depicted as a mass sitting on a rubber sheet, thus stretching the centre downwards. The greater the mass, the further down the rubber sheet is depressed. With a black hole, a sort of sink is formed on this rubber sheet due to the black hole's immense mass.
However, like many before, and many after, who worked on the physics behind black holes, Laplace and Hawking included, Einstein doubted the existence of such a physical body being possible, due to the requirement of the physical existence of a singularity. While his formulae allowed for their existence, he did not believe that nature would. This was not uncommon at the time and to give the actual existence of black holes much serious consideration was dangerous for a scientist's career.
Einstein presented his general relativity with ten field equations that describe the impact of gravity in a curved space-time. While addressing the issue of Mercury's shifting perihelion, he was only able to give an approximate solution to his equations. It may then have come as a pleasant surprise to Einstein when only a month after the publication of his theory, he received a letter from German physicist Karl Schwarzschild with his exact solution to the field equations. Einstein wrote back in 1916 [20]:-
I have read your paper with the utmost interest. I had not expected that one could formulate the exact solution of the problem in such a simple way. I liked very much your mathematical treatment of the subject. Next Thursday I shall present the work to the Academy with a few words of explanation.Within his solution, Schwarzschild introduced what would become known as the Schwarzschild radius, the radius defining the event horizon of a black hole. It is given as
where rs is the Schwarzschild radius, G is the universal gravitational constant, M is the mass of the of the body (in kilograms), and c is the speed of light.
Schwarzschild believed that the outward pressure exerted as matter was squeezed into a singularity would be sufficient to prevent a black hole actually forming. He reported that this problem of the formation of a black hole [1]:-
... was clearly not meaningful.Despite all the mathematical theory that had been developed for centuries prior, it would not be until after the mid-20th century that the possibility of a black hole's physical existence was generally accepted.
The debate over black holes' existence flared up between Indian American astrophysicist, then student of Cambridge University, Subrahmanyan Chandrasekhar, and English astronomer Arthur Eddington in the 1930s. Having seemingly befriended Chandrasekhar and encouraged his work at Cambridge, Eddington orchestrated a damning attack on the young astrophysicist's labours.
In 1930, on a voyage from India to England, Chandrasekhar had calculated that a white dwarf much heavier than the Sun could not exist, and that it would undergo a collapse into a singularity with infinite density. On 11 January 1935, with Eddington's apparent approval, Chandrasekhar was to deliver his results to a meeting of the Royal Astronomical Society in London. Little did he know, Eddington had prepared his own talk, and would give it directly following Chandrasekhar's.
Eddington belittled Chandrasekhar's argument, declaring that due to its solely mathematical basis, it had no bearing on the physical universe. How could something so large as a star effectively disappear? He upheld the view that white dwarfs could not totally collapse. Though Eddington's case was fairly unsubstantiated, the Briton's reputation prevented anyone from daring to openly disagree with him. Even Chandrasekhar was not given the chance to respond to Eddington's retort.
More information on the Chandrasekhar and Eddington dispute is given at THIS LINK.
Their rivalry on the matter continued for some years. At a meeting in Paris in 1939, Eddington maintained his disapproval of Chandrasekhar's ideas, despite the quiet, growing support for Chandrasekhar from the likes of Niels Bohr, Wolfgang Pauli and Paul Dirac. By this stage, it was widely believed that Eddington misunderstood the problem, thus he became largely ignored on this topic. At the meeting, Eddington claimed that there was no experimental test that could determine which of the two notions was correct. This was a valid point, but astronomer and white dwarf expert Gerard Kuiper was on hand to immediately refer to his work supporting Chandrasekhar. Eddington reluctantly apologised for hurting Chandrasekhar, but still refused to bow to his theory. Eddington's reluctance to accept what Chandrasekhar put forward supposedly had racial and sexually-repressive undertones, as well as stemming from the fact that acceptance of Chandrasekhar's argument would totally discredit what Eddington had been claiming for many years. No doubt an element of pride was present.
This condemnation of Chandrasekhar's suggestions by such an esteemed figure as Eddington possibly delayed the development of the black hole concept by decades. No-one followed up the claims made by Chandrasekhar, and the Indian himself turned to other fields, leaving Cambridge, where he felt his life and career had been harassed by racism, for Chicago. However, Canadian physicist Werner Israel, who studied in depth the scientific temper of these times, rejects this, claiming that Eddington's support would have made little difference to the sway of public opinion of Chandrasekhar's theory. Regardless, it would not be until 1983 that Chandrasekhar would be awarded the Nobel Prize for his work on white dwarfs.
Black holes had not even received their universal title until the 1960s. Previously known as 'darks stars', 'collapsars' and 'gravitationally completely collapsed objects' to name a few terms, the expression 'black hole' is popularly attributed to physicist John Wheeler, who admitted the term was offered to him by an audience member of one of his lectures in 1967. The use of the words 'black hole' had previously been used in 1963 at an astrophysics conference in Dallas, as claimed by science writer Marcia Bartusiak in [1]. Wheeler perhaps was merely the first with the scientific authority to use the phrase, hence its popularity took off and credit is often given to him. Just based on Google's Ngram viewer it can be seen that the use of the words 'black hole' in publications increased dramatically in and after the 1960s.

Chandrasekhar never opted to speculate what would happen to a star of sufficient mass, i.e. exceeding what would become known as the Chandrasekhar limit. This did not stop others from doing so however. Within two years of the discovery of the neutron by James Chadwick in 1932, German and Swiss astronomers, respectively Walter Baade and Fritz Zwicky, proposed the existence of neutron stars at a meeting of the American Physical Society. Whilst studying the cause of supernovae, they concluded that during such explosions, ordinary stars are turned into stars consisting of extremely closely packed neutrons, hence their name neutron star. A supernova can occur when a white dwarf in a binary star system essentially steals matter from its partner, gaining too much mass. Its core temperature rises enough to cause runaway nuclear fusion. Similar conclusions on neutron stars had also been made by Russian scientist Lev Davidovich Landau in 1931 before neutrons were discovered. He had also calculated that a star which was heavy enough could collapse to a point, but thinking this was ridiculous, he proposed that it would end up as a "one immense nucleus."
What's important is that at the time, a neutron star would be the densest object in the universe. While their existence was treated with the same hesitation as that of black holes, their observation would certainly help sway opinion over the possibility of the physical existence of black holes.
Moreover, just as Chandrasekhar had predicted an upper limit for white dwarfs, 1939 saw a paper in Physical Review by American theoretical physicist J Robert Oppenheimer and his graduate student at University of California, Berkley, George Volkoff, in which they predicted an equivalent constraint on neutron stars. They did not however know what would occur if a neutron star's mass exceeded this limit.
Following up this research, this time with a different graduate student, Hartland Snyder, Oppenheimer determined that if a star's core was more massive than two or three solar masses, then the stellar remnant would neither become a white dwarf nor a neutron star but would undergo "continued gravitational contraction." They calculated that mathematics predicted the such a star would continue to contract indefinitely leading to a singularity, the stuff of nightmares for physicists.
Though in this publication Oppenheimer and Snyder had offered the first modern description of black holes, the paper came out on 1 September 1939, the day of Germany's invasion of Poland triggering the start of the Second World War, and thus received little attention.
At this time, very few astronomers were ready to believe that such strange objects could exist in the real world. Even Einstein attempted to prove the impossibility of their existence in his paper published in 1939, only a month after Oppenheimer and Snyder's. However, Einstein had not even read Oppenheimer-Snyder, and his paper was considered as one of his worst. Stuck with the past's way of thinking, and with the teaching of relativity confined to mathematics rather than physics departments (or banned completely as happened during the Third Reich), most astronomers almost did not want such objects to be possible. It certainly helped their cause that there had yet to be any observations of neutron stars, let alone black holes.
Thus the work of British astronomer Jocelyn Bell can be considered important in the black hole concept's development. In 1967, she, along with radio astronomer Antony Hewish, picked up radio pulses from an unknown source. Initially dubbed LGM-1 (for "Little Green Men 1", since they considered the source could be an extraterrestrial civilisation), it was later found to be a rapidly rotating neutron star - the first observational evidence that neutron stars existed. Most of the known neutron stars have been found by detecting their regularly emitted radio pulses.
It was around this time that the tide was turning toward general acceptance of the possible existence of bodies such as black holes. Again using Google's Ngram viewer, when compared to other names used before 'black hole' was popularised, it can be inferred that worldwide acceptance of the concept of a black hole really only took off after the 1960s, since that was the first time any of the terms used for the concept became frequently used in publications.

More and more time was put into the study of black holes, including those of British theoretical physicist Stephen Hawking. By the end of the 1960s, both Werner Israel and British mathematician Roger Penrose with John Wheeler had helped revolutionise the study of black holes.
Israel, using general relativity, showed that non-rotating black holes had to be very simple; they were perfectly spherical, their size depended upon their mass only, and any two such black holes with the same mass must be identical. He, and many others, believed that the only way a black hole, which had to be perfectly spherical, could form was if it was created from the collapse of a perfectly spherical object. Thus any real star, which would never be perfectly spherical, would only ever collapse to form a naked singularity.
Penrose and Wheeler however argued that due to the rapid movements involved in a star's collapse, the gravitational waves given off would make it ever more and more spherical until it settled to a stationary state, where it would be perfectly spherical.
In 1970, Hawking, using quantum theory and general relativity, was able to show that black holes can actually emit radiation, giving a theoretical argument for their existence in 1974. This is the prediction for what is now know as Hawking Radiation. By radiating, black holes conserve entropy, solving the incompatibility problem with the second law of thermodynamics. This added to the argument for their physical existence.
According to quantum physics, particle-antiparticle pairs are constantly being produced throughout the universe. What happens in nearly every case is that they almost instantly annihilate with each other, releasing energy into the universe. Hawking postulated that were such a particle pair to form near a black hole's event horizon, then before given the chance to annihilate, one of the pair could be dragged toward the black hole's singularity, while the other escapes. It is in this form that black holes are said to radiate. This challenges what general relativity says about nothing being able to escape from the clutches of a black hole. Moreover, Hawking stated that since a black hole radiates in such a manner, it shrinks, evaporating until it vanishes.
Naturally, as with most discoveries in this field, Hawking Radiation poses yet more unanswered questions. If a black hole shrinks, what happens to the information that was put into it? This leads to the information paradox since quantum mechanics says information cannot be deleted.
Despite all the doubt throughout the many years of work on black holes, the likelihood of their physical reality is almost certain. What is now widely accepted as the first discovered black hole, Cygnus X-1 was first 'seen' in 1964, and was generally recognised as a black hole by the 1990s. It was the subject of a bet in 1974 between Hawking and American theoretical physicist Kip Thorne, which Hawking conceded in 1990, admitting that Cygnus X-1 was indeed in all likelihood a black hole, based on the sufficient observational data they had.
Further support has been offered by the Hubble Space Telescope (HST) not just in verifying black holes' existence, but also in backing up claims made since the 1960s regarding galaxies each containing a supermassive black hole at their centre. Launched in 1990, the HST has allowed astronomers to conclude that black holes are probably common to the centres of all galaxies.
One of the latest observational discoveries in this field has come from the LIGO (Laser Interferometer Gravitational-Wave Observatory) and Virgo Scientific Collaboration. Observed on 14 September 2015, the Collaboration announced on 11 February 2016 that they had made the first observational discovery of gravitational waves (disturbances in the curvature of space-time generated by accelerated masses). They had emerged from a collision of two black holes. This offered the first observational evidence for the existence of binary black hole systems. In 2017, Kip Thorne was one of three (Thorne, Barry Barish, Rainer Weiss) to receive the Nobel Prize for contribution to the detection of gravitational waves.
It is still unclear how singularities apply in reality. This poses the question over the limit of mathematics' ability to fully model nature. Alternatively, singularities imply that we have yet to develop a complete description of the universe and its workings: it may be that some of the notions we take as firm truths are just not quite correct.
The concept of a black hole has overcome a great deal of resistance to get to the point of acceptance it enjoys today. With its conceptual development, a large number of scientists have made their name bringing what was initially just a mathematical concept, ridiculed for its lack of physical meaning, into the forefront as one of astronomy's most exciting realities, questioning long held beliefs of the workings of the universe. Resistance was futile; black holes are inescapable.
References (show)
- M Bartusiak, Black Hole: How an idea abandoned by Newtonians, hated by Einstein, and gambled on by Hawking became loved (Yale University Press, New Haven-London, 2015).
- M Begelman and M Rees, Gravity's Fatal Attraction: Black Holes in the Universe (Scientific American Library, New York, 1996).
- S Chandrasekhar, The Mathematical Theory of Black Holes (Clarendon Press, 1998).
- J M Galat, Black Holes and Supernovas (Capstone, 2011).
- S S Gubser and F Pretorius, The Little Book of Black Holes (Princeton University Press, 2017).
- S Hawking, A Brief History of Time (Bantam Press, London-New York, 1988).
- S Hawking, Black Holes: The Reith Lectures (Random House, 2016).
- S Latta, Black Holes: The Weird Science of the Most Mysterious Objects in the Universe (Twenty-First Century Books, 2017).
- A I Miller, Empire of the Stars: Obsession, Friendship, and Betrayal in the Quest for Black Holes (Houghton Mufflin, Boston, 2005).
- D Nardo, Black Holes (Independent Publishing Platform, 2015).
- I D Novikov, Black Holes and the Universe (Cambridge University Press, Cambridge, 1995).
- C Oxlade, The Mystery of Black Holes (Heinemann Library, 1999).
- D J Raine and E G Thomas, Black Holes: An Introduction (Imperial College Press, 2010).
- D M Rau, Black Holes (Capstone, 2015).
- K S Thorne, Black Holes and Time Warps: Einstein's Outrageous Legacy (W W Norton, 1994).
- W H Tucker, Chandra's Cosmos: Dark Matter, Black Holes, and Other Wonders Revealed by NASA's Premier X-Ray Observatory (Smithsonian Institution, 2017).
- S Chandrasekhar, The Black Hole in Astrophysics: The Origin of the Concept and its Role, Contemporary Physics 15 (1974), 1-24.
- A Chodos (ed.), 1783: John Michell anticipates black holes, Physics History 18 (10) (2009).
- F Dyson, Chandrasekhar's role in 20th-century science, Physics Today 63 (12) (2010), 44-48.
- J Eisenstaedt, The Early Interpretation of the Schwarzschild Solution, in D Howard and J Stachel (eds), Einstein and the History of General Relativity: Einstein Studies 1 (Birkhauser, Boston, 1989), 213-233.
- M Finkel, Star Eater, National Geographic Magazine (March 2014).
- P Gilster, Cygnus X-1: A Black Hole Confirmed, Centauri Dreams, centauri-dreams.org. https://www.centauri-dreams.org/2011/11/29/cygnus-x-1-a-black-hole-confirmed/
- S Hossenfelder, Are Singularities Real?, The Nature of Reality, PBS (9 December 2015).
- J McClintock, Do Black Hole exist?, Sky and Telescope (January 1988), 28-33.
- A I Miller, S Chandrasekhar: the student who took on the world's top astrophysicist, The Guardian (19 October 2017).
- C Montgomery, W Orchiston and I Whittingham, Michell, Laplace and the origin of the black hole concept, Journal of Astronomical History and Heritage 12 (2) (2009), 90-96.
- S Schaffer, John Mitchell and Black Holes, Journal for the History of Astronomy 10 (1979), 42-43.
- T Siegfried, 50 years later, it's hard to say who named black holes, Science News magazine (23 December 2013).
- S Soter and N deGrasse Tyson, Case Study: John Michell And Black Holes, Cosmic Horizons: Astronomy at the Cutting Edge, American Museum of Natural History (2000).https://www.amnh.org/explore/resource-collections/cosmic-horizons/case-study-john-michell-and-black-holes
- K Subramanian, Before S Chandrasekhar won the Nobel in 1983 his theories were overlooked because of his race, Business Standard (20 October 2017).
- A Sundermier, Black Holes, Symmetry Magazine (1 December 2016).
- What Is a Black Hole? NASA Knows! (Grades 5-8), NASA (4 June 2014). https://www.nasa.gov/audience/forstudents/5-8/features/nasa-knows/what-is-a-black-hole-58.html
Written by J G Mena and T S C Peres, University of St Andrews
Last Update November 2018
Last Update November 2018