Indian Mathematics - Redressing the balance
Ian G Pearce
Mathematics in the service of religion: I. Vedas and Vedangas
The Vedic religion was followed by the Indo-Aryan peoples, who originated from the north of the sub-continent. It is through the works of Vedic religion that we gain the first literary evidence of Indian culture and hence mathematics. Written in Vedic Sanskrit the Vedic works, Vedas and Vedangas (and later Sulbasutras) are primarily religious in content, but embody a large amount of astronomical knowledge and hence a significant knowledge of mathematics. The requirement for mathematics was (at least at first) twofold, as R Gupta discusses:
Some chronological confusion exists with regards to the appearance of the Vedic religion. S Kak states in a very recent work that the time period for the Vedic religion stretches back potentially as far as 8000BC and definitely 4000BC. Whereas G Joseph states 1500 BC as the forming of the Hindu civilisation and the recording of Vedas and Vedangas, and later Sulbasutras. However it seems most likely that significant knowledge of astronomy and mathematics first appears in Vedic works around the 2nd millennium BC. The Rg-Veda (fire altar) the earliest extant Vedic work dates from around 1900 BC. R Gupta in his paper on the problem of ancient Indian chronology shows that dates from 26000-200 BC have been suggested for the Vedic 'period'. Having consulted many sources I am confident at placing the period of the Vedas (and Vedangas) at around 1900-1000 BC.
Further mathematical work is found in the Sulbasutras of the later Vedic period, the earliest of which is thought to have been written around 800 BC and the last around 200 BC. I will now move on from this slightly clouded chronological discussion. It is however worth noting that there are serious underlying problems with the chronology of early Indian mathematics which require significant attention.
Although the requirement of mathematics at this time was clearly not for its own sake, but for the purposes of religion and astronomy, it is important not to ignore the secular use of the texts, i.e. by the craftsmen who were building the altars. Similarly with the earlier Harappan peoples it seems likely that (at least) basic mathematics will have grown to become used by large numbers of the population. Regardless of the fact that at this time mathematics remained for practical uses, some significant work in the fields of geometry and arithmetic were developed during the Vedic period and as L Gurjar states:
It is also worthwhile briefly noting the astronomy of the Vedic period which, given very basic measuring devices (in many cases just the naked eye), gave surprisingly accurate values for various astronomical quantities. These include the relative size of the planets the distance of the earth from the sun, the length of the day, and the length of the year. For further information, S Kak is an authority on the astronomical content of Vedic works.
Much of the mathematics contained within the Vedas is found in works called Vedangas of which there are six. Of the six Vedangas those of particular significance are the Vedangas Jyotis and Kalpa (the fifth and sixth Vedangas). Jyotis was (at the time) the name for astronomy, while Kalpa contained the rules for the rituals and ceremonies. The Vedangas are best described as an auxiliary to the Vedas.
N Dwary claims, with reference to the Vedanga-Jyotis, that:
S Kak suggests a date of around 1350 BC for the Vedanga-Jyotis. I include this as a reminder of the time period being discussed.
Along with the Vedangas there are several further works that contain mathematics, including:
Of these the Taittiriya Samhita and Rg-Veda are considered the oldest and contain rules for the construction of great fire altars.
Figure 4.1.1: First layer of a Vedic sacrificial altar (in the shape of a falcon). [GJ, P 227]
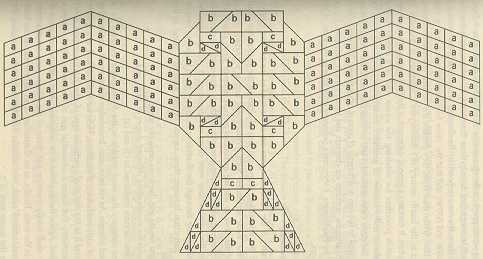
As a result of the mathematics required for the construction of these altars, many rules and developments of geometry are found in Vedic works. These include:
S Kak gives three values for from the Satapatha Brahmana. It seems most probable that they arose from transformations of squares into circles and circles to squares. The values are:
Astronomical calculations also leads to a further Vedic approximation:
This is correct (when rounded) to 2 decimal places.
Also found in Vedic works are:
The Arab scholar Al-Biruni (973-1084 AD) discovered that only the Indians had a number system that was capable of going beyond the thousands in naming the orders in decimal counting.
Evidence of the use of this advanced numerical concept leads S Sinha to comment:
It is in Vedic works that we also first find the term "ganita" which literally means "the science of calculation". It is basically the Indian equivalent of the word mathematics and the term occurs throughout Vedic texts and in all later Indian literature with mathematical content.
Among the other works I have mentioned, mathematical material of considerable interest is found:
...The need to determine the correct times for Vedic ceremonies and the accurate construction of altars led to the development of astronomy and geometry. [RG2, P 131]
Some chronological confusion exists with regards to the appearance of the Vedic religion. S Kak states in a very recent work that the time period for the Vedic religion stretches back potentially as far as 8000BC and definitely 4000BC. Whereas G Joseph states 1500 BC as the forming of the Hindu civilisation and the recording of Vedas and Vedangas, and later Sulbasutras. However it seems most likely that significant knowledge of astronomy and mathematics first appears in Vedic works around the 2nd millennium BC. The Rg-Veda (fire altar) the earliest extant Vedic work dates from around 1900 BC. R Gupta in his paper on the problem of ancient Indian chronology shows that dates from 26000-200 BC have been suggested for the Vedic 'period'. Having consulted many sources I am confident at placing the period of the Vedas (and Vedangas) at around 1900-1000 BC.
Further mathematical work is found in the Sulbasutras of the later Vedic period, the earliest of which is thought to have been written around 800 BC and the last around 200 BC. I will now move on from this slightly clouded chronological discussion. It is however worth noting that there are serious underlying problems with the chronology of early Indian mathematics which require significant attention.
Although the requirement of mathematics at this time was clearly not for its own sake, but for the purposes of religion and astronomy, it is important not to ignore the secular use of the texts, i.e. by the craftsmen who were building the altars. Similarly with the earlier Harappan peoples it seems likely that (at least) basic mathematics will have grown to become used by large numbers of the population. Regardless of the fact that at this time mathematics remained for practical uses, some significant work in the fields of geometry and arithmetic were developed during the Vedic period and as L Gurjar states:
...The Hindu had made enormous strides in the field of mathematics. [LG, P 2]
It is also worthwhile briefly noting the astronomy of the Vedic period which, given very basic measuring devices (in many cases just the naked eye), gave surprisingly accurate values for various astronomical quantities. These include the relative size of the planets the distance of the earth from the sun, the length of the day, and the length of the year. For further information, S Kak is an authority on the astronomical content of Vedic works.
Much of the mathematics contained within the Vedas is found in works called Vedangas of which there are six. Of the six Vedangas those of particular significance are the Vedangas Jyotis and Kalpa (the fifth and sixth Vedangas). Jyotis was (at the time) the name for astronomy, while Kalpa contained the rules for the rituals and ceremonies. The Vedangas are best described as an auxiliary to the Vedas.
N Dwary claims, with reference to the Vedanga-Jyotis, that:
...Hindus of the period were fully conversant with fundamental operations of arithmetic. [ND1, P 39]
S Kak suggests a date of around 1350 BC for the Vedanga-Jyotis. I include this as a reminder of the time period being discussed.
Along with the Vedangas there are several further works that contain mathematics, including:
Taittiriya Samhita
Satapatha Brahmana and
Yajur and Atharva-Veda
Rg-Veda (of which it is thought there are three 'versions') plus additional
Samhitas
Of these the Taittiriya Samhita and Rg-Veda are considered the oldest and contain rules for the construction of great fire altars.
Figure 4.1.1: First layer of a Vedic sacrificial altar (in the shape of a falcon). [GJ, P 227]

As a result of the mathematics required for the construction of these altars, many rules and developments of geometry are found in Vedic works. These include:
Use of geometric shapes, including triangles, rectangles, squares, trapezia and circles.
Equivalence through numbers and area.
Equivalence led to the problem of:
Squaring the circle and visa-versa.
Early forms of Pythagoras theorem.
Estimations for .
S Kak gives three values for from the Satapatha Brahmana. It seems most probable that they arose from transformations of squares into circles and circles to squares. The values are:
Astronomical calculations also leads to a further Vedic approximation:
This is correct (when rounded) to 2 decimal places.
Also found in Vedic works are:
All four arithmetical operators (addition, subtraction, multiplication and division).
A definite system for denoting any number up to 1055 and existence of zero.
Prime numbers.
The Arab scholar Al-Biruni (973-1084 AD) discovered that only the Indians had a number system that was capable of going beyond the thousands in naming the orders in decimal counting.
Evidence of the use of this advanced numerical concept leads S Sinha to comment:
...It is fair to agree that a nation with such an advanced and cultured civilisation and which was using the numerical system (decimal place value) knew also how to handle the associated arithmetic. [SS1, P 73]
It is in Vedic works that we also first find the term "ganita" which literally means "the science of calculation". It is basically the Indian equivalent of the word mathematics and the term occurs throughout Vedic texts and in all later Indian literature with mathematical content.
Among the other works I have mentioned, mathematical material of considerable interest is found:
Arithmetical sequences, the decreasing sequence 99, 88, ... , 11 is found in the Atharva-Veda.
Pythagoras's theorem, geometric, constructional, algebraic and computational aspects known. A rule found in the Satapatha Brahmana gives a rule, which implies knowledge of the Pythagorean theorem, and similar implications are found in the Taittiriya Samhita.
Fractions, found in one (or more) of the Samhitas.
Equations, for example, found in one of the Samhitas.
The 'rule of three'.