Indian Mathematics - Redressing the balance
Ian G Pearce
Mathematics in the service of religion: II. Sulba Sutras
The later Sulba-sutras represent the 'traditional' material along with further related elaboration of Vedic mathematics. The Sulba-sutras have been dated from around 800-200 BC, and further to the expansion of topics in the Vedangas, contain a number of significant developments.
These include first 'use' of irrational numbers, quadratic equations of the form a x2 = c and ax2 + bx = c, unarguable evidence of the use of Pythagoras theorem and Pythagorean triples, predating Pythagoras (c 572 - 497 BC), and evidence of a number of geometrical proofs. This is of great interest as proof is a concept thought to be completely lacking in Indian mathematics.
Example 4.2.1: Pythagoras theorem and Pythagorean triples, as found in the Sulba Sutras.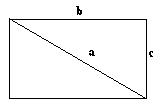
Examples of Pythagorean triples given as the sides of right angled triangles:
It is thought that the Sulvas were intended to supplement the Kalpa (the sixth Vedanga), and their primary content remained instructions for the construction of sacrificial altars. The name Sulvasutra means 'rule of chords' which is another name for geometry.
N Dwary states:
R Gupta similarly claims:
With reference to the possible appearance of proof is a quote from A Michaels:
This is not particularly compelling evidence but does suggest that the composers of the sulba-sutras may have had a greater depth of knowledge than is generally thought.
Many suggestions for the value of p are found within the sutras. They cover a surprisingly wide range of values, from 2.99 to 3.2022.
Pythagoras's theorem and Pythagorean triples arose as the result of geometric rules. It is first found in the Baudhayana sutra - so was hence known from around 800 BC. It is also implied in the later work of Apastamba, and Pythagorean triples are found in his rules for altar construction. Altar construction also led to the discovery of irrational numbers, a remarkable estimation of √2 in found in three of the sutras. The method for approximating the value of √2 gives the following result:
This is equal to 1.412156..., which is correct to 5 decimal places.
It has been argued by scholars seemingly attempting to deprive Indian mathematics of due credit, that Indians believed that exactly, which would not indicate knowledge of the concept of irrationality. Elsewhere in Indian works however it is stated that various square root values cannot be exactly determined, which strongly suggests an initial knowledge of irrationality.
Indeed an early method for calculating square roots can be found in some Sutras, the method involves repeated application of the formula: , r being small.
Example 4.2.2: Application of formula for calculating square roots.
C Srinivasiengar thus states:
Many of the Vedic contributions to mathematics have been neglected or worse. When it first became apparent that there was geometry contained within works that was not of Greek origin, historians and mathematical commentators went to great lengths to try and claim that this geometry was Greek influenced (to a greater or lesser extent).
It is undeniable that none of the methods of Greek geometry are discernible in Vedic geometry, but this merely serves to support arguments that it is independently developed and not in some way borrowed from Greek sources.
In light of recent evidence and more accurate dating it has been even more strongly claimed by A Seidenberg (in S Kak) that:
This may be a somewhat extreme standpoint, and it seems likely that there was traffic of ideas in all directions of the Ancient world, but there is little doubt that the vast majority of Indian work is original to its writers. It may lack the cold logic and truly abstract character of modern mathematics but this observation further helps to identify it as uniquely Indian. Of all the mathematics contained in the Vedangas it is the definite appearance of decimal symbols for numerals and a place value system that should perhaps be considered the most phenomenal.
Before the period of the Sulbasutras was at an end the Brahmi numerals had definitely begun to appear (c. 300BC) and the similarity with modern day numerals is clear to see (see Figures 7.1 and 7.3). More importantly even still was the development of the concept of decimal place value. M Pandit in a recent paper (discussed in RG2) has shown certain rules given by the famous Indian grammarian Panini (c. 500 BC) imply the concept of the mathematical zero. Further to this there is a small amount of evidence of the use of symbols for numbers even earlier in the Harrapan culture. My evidence comes primarily from a paper by S Kak, which analyses some of Panini's work, and there is further support from a paper by S Sinha. B Datta and A Singh also give evidence of an early emergence of numerical forms and the decimal place value system.
These include first 'use' of irrational numbers, quadratic equations of the form a x2 = c and ax2 + bx = c, unarguable evidence of the use of Pythagoras theorem and Pythagorean triples, predating Pythagoras (c 572 - 497 BC), and evidence of a number of geometrical proofs. This is of great interest as proof is a concept thought to be completely lacking in Indian mathematics.
Example 4.2.1: Pythagoras theorem and Pythagorean triples, as found in the Sulba Sutras.
The rope stretched along the length of the diagonal of a rectangle makes an area which the, vertical and horizontal sides make together.
In other words: .

Examples of Pythagorean triples given as the sides of right angled triangles:
5, 12, 13
8, 15, 17
12, 16, 20
12, 35, 37
Of the Sulvas so far 'uncovered' the four major and most mathematically significant are those composed by Baudhayana, Manava, Apastamba and Katyayana (perhaps least 'important' of the Sutras, by the time it was composed the Vedic religion was becoming less predominant). However in a paper written 20 years ago S Sinha claims that there are a further three Sutras, 'composed' by Maitrayana, Varaha and Vadhula (SS1, P 76). I have yet to come across any other references to these three 'extra' sutras. These men were not mathematicians in the modern sense but they are significant none the less in that they were the first mentioned 'individual' composers. E Robertson and J O'Connor have suggested that they were Vedic priests (and skilled craftsmen).
8, 15, 17
12, 16, 20
12, 35, 37
It is thought that the Sulvas were intended to supplement the Kalpa (the sixth Vedanga), and their primary content remained instructions for the construction of sacrificial altars. The name Sulvasutra means 'rule of chords' which is another name for geometry.
N Dwary states:
...They offer a wealth of geometrical as well as arithmetical results. [ND1, P 40]
R Gupta similarly claims:
...The Sulba-sutras are (quite) rich in mathematical contents. [RG2, P 133]
With reference to the possible appearance of proof is a quote from A Michaels:
...Vedic geometry, though non-axiomatic in character, is provable and indeed proof is implicit in several constructions prescribed in the Sulba-sutras. [RG2, P 133]
This is not particularly compelling evidence but does suggest that the composers of the sulba-sutras may have had a greater depth of knowledge than is generally thought.
Many suggestions for the value of p are found within the sutras. They cover a surprisingly wide range of values, from 2.99 to 3.2022.
Pythagoras's theorem and Pythagorean triples arose as the result of geometric rules. It is first found in the Baudhayana sutra - so was hence known from around 800 BC. It is also implied in the later work of Apastamba, and Pythagorean triples are found in his rules for altar construction. Altar construction also led to the discovery of irrational numbers, a remarkable estimation of √2 in found in three of the sutras. The method for approximating the value of √2 gives the following result:
This is equal to 1.412156..., which is correct to 5 decimal places.
It has been argued by scholars seemingly attempting to deprive Indian mathematics of due credit, that Indians believed that exactly, which would not indicate knowledge of the concept of irrationality. Elsewhere in Indian works however it is stated that various square root values cannot be exactly determined, which strongly suggests an initial knowledge of irrationality.
Indeed an early method for calculating square roots can be found in some Sutras, the method involves repeated application of the formula: , r being small.
Example 4.2.2: Application of formula for calculating square roots.
If A=10, take a = 3 and r = 1.
Thus = 3.16667 in (modern) decimal notation.
√10 = 3.162278 to six decimal places when calculated on a calculator.
Thus, after only one application of the formula, a moderately accurate value has been calculated.
Thus = 3.16667 in (modern) decimal notation.
√10 = 3.162278 to six decimal places when calculated on a calculator.
Thus, after only one application of the formula, a moderately accurate value has been calculated.
C Srinivasiengar thus states:
... The credit of using irrational numbers for the first time must go to the Indians. [CS, P 15]
Many of the Vedic contributions to mathematics have been neglected or worse. When it first became apparent that there was geometry contained within works that was not of Greek origin, historians and mathematical commentators went to great lengths to try and claim that this geometry was Greek influenced (to a greater or lesser extent).
It is undeniable that none of the methods of Greek geometry are discernible in Vedic geometry, but this merely serves to support arguments that it is independently developed and not in some way borrowed from Greek sources.
In light of recent evidence and more accurate dating it has been even more strongly claimed by A Seidenberg (in S Kak) that:
... Indian geometry and mathematics pre-dates Babylonian and Greek mathematics. [SK1, P 338]
This may be a somewhat extreme standpoint, and it seems likely that there was traffic of ideas in all directions of the Ancient world, but there is little doubt that the vast majority of Indian work is original to its writers. It may lack the cold logic and truly abstract character of modern mathematics but this observation further helps to identify it as uniquely Indian. Of all the mathematics contained in the Vedangas it is the definite appearance of decimal symbols for numerals and a place value system that should perhaps be considered the most phenomenal.
Before the period of the Sulbasutras was at an end the Brahmi numerals had definitely begun to appear (c. 300BC) and the similarity with modern day numerals is clear to see (see Figures 7.1 and 7.3). More importantly even still was the development of the concept of decimal place value. M Pandit in a recent paper (discussed in RG2) has shown certain rules given by the famous Indian grammarian Panini (c. 500 BC) imply the concept of the mathematical zero. Further to this there is a small amount of evidence of the use of symbols for numbers even earlier in the Harrapan culture. My evidence comes primarily from a paper by S Kak, which analyses some of Panini's work, and there is further support from a paper by S Sinha. B Datta and A Singh also give evidence of an early emergence of numerical forms and the decimal place value system.