Curves
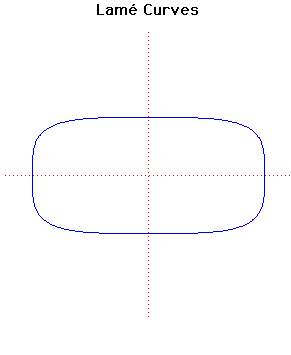
Lame Curves
Description
In 1818 Lamé discussed the curves with equation given above. He considered more general curves than just those where is an integer. If is a rational then the curve is algebraic but, for irrational , the curve is transcendental.The curve drawn above is the case . For even integers the curve becomes closer to a rectangle as increases. For odd integer values of the curve looks like the even case in the positive quadrant but goes to infinity in both the second and fourth quadrants.
The case is the Astroid, while the case is the (so-called) Witch of Agnesi.
The case has been associated with the Danish architect and poet Piet Hein (inventor of the Soma Cube) under the name of superellipse and have been used for a variety of purposes, including motorway bridges and other architectural applications.