Mathematics and Architecture
Although many readers of this archive might find an article on mathematics and architecture a little surprising, in fact architecture was in ancient times considered a mathematical topic and the disciplines have, up to the present time, retained close connections. Perhaps once one realises that mathematics is essentially the study of patterns, the connection with architecture becomes clearer. Salingaros writes in [27]:-
One has to make decisions as to whether the numerical coincidences are really coincidences, or whether the builders of the pyramids designed them with certain numerical ratios in mind. Let us look at just one such coincidence involving the golden number. The golden number is (1 + √5)/2 = 1.618033989 and an angle based on this will have size arcsec(1.618033989) = 51° 50'. Now the sides of the Great Pyramid rise at an angle of 51° 52'. Is this a coincidence? F Röber, in 1855, was the first to argue that the golden number had been used in the construction of the pyramids. Many authors have followed Röber, or produced even more elaborate versions of how and the golden number have been utilised by the Egyptians. The authors of [23], however, suggest reasons for the occurrence of many of the nice numbers, in particular numbers close to powers of the golden number, as arising from the building techniques used rather than being deliberate decisions of the architects. Arguments of this type have appeared more frequently in recent years.
Even if deep mathematical ideas went into the construction of the pyramids, I think that Ifrah makes a useful contribution to this debate in [4] when he writes:-
Numbers for Pythagoras also had geometrical properties. The Pythagoreans spoke of square numbers, oblong numbers, triangular numbers etc. Geometry was the study of shapes and shapes were determined by numbers. But more than this, the Pythagoreans developed a notion of aesthetics based on proportion. In addition geometrical regularity expressed beauty and harmony and this was applied to architecture with the use of symmetry. Now symmetry to a mathematician today suggests an underlying action of a group on a basic configuration, but it is important to realise that the word comes from the ancient Greek architectural term "symmetria" which indicated the repetition of shapes and ratios from the smallest parts of a building to the whole structure. It should now be clear what the belief that "all things are numbers" meant to the Pythagoreans and how this was to influence ancient Greek architecture.
Let us look briefly at the dimensions of the Parthenon to see how the lengths conform to the mathematical principles of proportion of the Pythagoreans. In 480 BC the Acropolis in Athens was totally destroyed by the Persians in the Second Persian War. To understand the timescale, let us note that this was about the time of the death of Pythagoras. After the Greek victory over the Persian at Salamis and Plataea the Greeks did not begin the reconstruction of the city of Athens for several years. Only after the Greek states ended their fighting in the Five Years' Truce of 451 BC did the conditions exist to encourage reconstruction. Pericles, the Head of State in Athens, set about rebuilding the temples of the Parthenon in 447 BC. The architects Ictinus and Callicrates were employed, as was the sculptor Phidias.
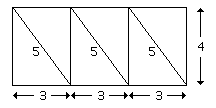
Berger, in [11], makes a study of the way that the Pythagorean ideas of ratios of small numbers were used in the construction of the Temple of Athena Parthenos. The ratio 2 : 3 and its square 4 : 9 were fundamental to the construction. A basic rectangle of sides 4 : 9 was constructed from three rectangles of sides 3 and 4 with diagonal 5. This form of construction also meant that the 3 : 4 : 5 Pythagorean triangle could be used to good effect to ensure that right angles in the building were accurately determined.
The length of the Temple is 69.5 m, its width is 30.88 m and the height at the cornice is 13.72 m. To a fairly high degree of accuracy this means that the ratio width : length = 4 : 9 while also the ratio height : width = 4 : 9. Berger took the greatest common denominator of these measurements to arrive at the ratios
We mentioned above that F Röber believed that the Egyptians had used the golden number in their construction of the pyramids. In the same work of 1855 he also argued that the golden number was used in the construction of the Temple of Athena on the Parthenon. Perhaps this work was very persuasive, or perhaps it presented a romantic idea which people wanted to believe. Whatever the reason, it appears as essentially an accepted fact today by most people that indeed the buildings of the Parthenon achieved their undoubted exceptional beauty through the use of the golden number. There appears little hard evidence to support this view, while Berger's 4 : 9 theory, on the other hand, appears well established.
Plato was much influenced by the ideas of Pythagoras. Plato's theory of ideas makes meaning and concepts as fundamental and real, while the physical realisation of these ideas was not real and of lesser importance. For example the idea of a flower is real and permanent while the physical examples of flowers are only seen as apparent and temporary. Although buildings are not permanent, Plato saw that they were long lasting and therefore more beautiful to him than flowers. He saw mathematics as providing the most fundamental of all ideas and therefore buildings should be designed on mathematical principles. Plato writes in Philebus:-
It is interesting, particularly given the details above on how the Temple of Athena on the Parthenon was constructed, to look at what Vitruvius says in Book 3 on designing temples. The book begins with an essay on symmetry and then describes the use of symmetry and proportion in the design of temples. For Vitruvius the proportions of the human body were fundamental in achieving beauty and he says that the proportions of the temple should follow these human proportions. He suggests that the circle and the square are perfect figures for generating architectural designs because they approximate the geometry of the spread-eagled human body. There is a religious significance here, since Vitruvius believed that the human body was made in the image of a god and was therefore perfect. Of course many have argued that the golden number can be found in the proportions of the human body so it may be that the evidence found today for the golden number in ancient Greek temples is explained by its relation to human proportions.
One of the remarkable parts of De architectura Ⓣ is Book 5 where Vitruvius discusses acoustics. Sarton writes [6]:-
In Europe there was little progress in mathematics and architecture until the 14th and 15th Centuries. Architecture was modelled on the teachings of Vitruvius and on the classical architecture which was still plentiful, particularly in Greece and Italy. The next person we want to mention is Brunelleschi who was trained as a goldsmith. There were really no professional architects at this time and Brunelleschi learnt his skills in architecture by visiting Rome:-
Although the name of Leonardo da Vinci makes one think of his stunning paintings rather than mathematics, in fact he was fascinated by mathematics. Architecture was another of his specialities and he learnt about it, in particular the mathematical principles behind it, from studying Alberti's texts. He was a man of wide ranging abilities and interests and, at one stage in his career, earned his living advising the Duke of Milan on architecture, fortifications and military matters. He was also considered as a hydraulic and mechanical engineer. He also worked for Cesare Borgia as a military architect and general engineer. Later the French King Francis I appointed him first painter, architect, and mechanic to the King.
Another mathematician from Renaissance times was Bombelli who was taught by Pier Francesco Clementi, himself an engineer and architect. With this training Bombelli was soon working himself as both engineer and architect employing his mathematical skills both in his work and in his deep investigation of complex numbers. Another to combine his skills in both mathematics and architecture was Bramer who was employed directing constructions of fortifications and castles. He published a work on the calculation of sines, prompted by the practical work in which he was involved. He followed Alberti (1435), Dürer (1525) and Bürgi (1604) when in 1630 he constructed a mechanical device that enabled one to draw accurate geometric perspective.
La Faille was a contemporary of Bramer who taught mathematics and military engineering. He worked as an architect advising on fortifications and he wrote an architectural treatise as well as important works on mechanics. Later in the 17th Century lived the English architect Wren, in many ways the best known architect in English history. A well rounded scientist, he solved a number of important mathematical problems before taking up architecture as a profession. Although he is better known as an architect than as a mathematician he was considered one of the leading mathematicians of his day by Newton. It was clear that Wren saw mathematics as being a subject which had applications to a wide variety of scientific disciplines and his mathematical skills played an important role in his architectural achievements. One of the architects with whom he worked, Robert Hooke, is better known as a mathematician than as an architect. Again that mathematics and architecture were closely related disciplines was considered natural at this time.
Another 17th Century mathematician was La Hire whose interests geometry arose from his study of architecture. In 1687 he was appointed to the chair of architecture at the Académie Royale. His interest in geometry arose from his study of perspective and he went on to make important contributions to conic sections. In the 18th century Poleni made contributions to hydraulics, physics, astronomy and archaeology. He held university chairs in astronomy, physics and mathematics as well as working as an architect.
The nineteenth century saw a change of attitude which led to a separation in people's minds of the scientific and the artistic. From this period the roles of mathematicians and architects were seen as distinct in a way that did not happen in say the seventeenth century. This is not to say that the connections between mathematics and architecture vanished, just that the scientific and artistic aspects were seen as complementary skills not to be found in the same person. Of course there were still those who did excel in mathematics and architecture; it was only perceptions which changed. An example of a person who excelled in architecture and mathematics was Aronhold who taught at the Royal Academy of Architecture at Berlin from 1851. Aronhold was appointed professor at the Royal Academy of Architecture in 1863. He made outstanding contributions to geometry.
Others from this period who combined the two skills include Brioschi and Wiener. From 1852 to 1861 Brioschi was professor of applied mathematics at the University of Pavia. There he taught mechanics, architecture and astronomy. Wiener studied engineering and architecture at the University of Giessen from 1843 to 1847. With this training he went on to become a teacher of physics, mechanics, hydraulics and descriptive geometry at the Technische Hochschule in Darmstadt.
There are a number of late 19th Century, and 20th Century mathematician who began their careers as architects before turning to mathematics, for example the Frenchman Drach and the American Wilks. Drach worked as an architect before turning to mathematics. Wilks studied architecture at North Texas State Teachers College. He received a B.A. in architecture in 1926. However his eyesight was not too good, and he feared that this would be a handicap if he pursued architecture as a profession so he decided on a career in mathematics.
Two unique talents from the 20th Century were Escher and Buckminster Fuller. Escher was never a mathematician, despite his fascination with the subject and the deep mathematical ideas which underlay his art. He trained at the School of Architecture and Decorative Arts in Haarlem and only at age 21 did he give up architecture in favour of art. Buckminster Fuller was an engineer, mathematician and architect who applied geometric principles to design a totally new concept in buildings in the second half of the 20th Century. He made an art out of structural purity, using simple geometric forms for aesthetic as well as functional purposes.
Historically, architecture was part of mathematics, and in many periods of the past, the two disciplines were indistinguishable. In the ancient world, mathematicians were architects, whose constructions - the pyramids, ziggurats, temples, stadia, and irrigation projects - we marvel at today. In Classical Greece and ancient Rome, architects were required to also be mathematicians. When the Byzantine emperor Justinian wanted an architect to build the Hagia Sophia as a building that surpassed everything ever built before, he turned to two professors of mathematics (geometers), Isidoros and Anthemius, to do the job. This tradition continued into the Islamic civilization. Islamic architects created a wealth of two-dimensional tiling patterns centuries before western mathematicians gave a complete classification.The first mentioned type of architecture Salingaros mentions in this quote is the pyramid and here we have marked disagreement between experts on the how much geometry and number theory the architects used. For example the Great Pyramid was built at Giza in Egypt around 2575 BC for King Khufu. Much has been written on the measurements of this pyramid and many coincidences have been found with , the golden number and its square root. There are at least nine theories which claim to explain the shape of the Pyramid and at least half of these theories agree with the observed measurements to one decimal place. This is a difficult area, for there is no doubt about certain astronomical alignments in the construction of the pyramid. Also regular geometric shapes were sacred to the Egyptians and they reserved their use in architecture for ritual and official buildings. That they had a goddess of surveying, called Seschat, shows the religious importance placed on building. However, no proof exists that sophisticated geometry lies behind the construction of the pyramids.
One has to make decisions as to whether the numerical coincidences are really coincidences, or whether the builders of the pyramids designed them with certain numerical ratios in mind. Let us look at just one such coincidence involving the golden number. The golden number is (1 + √5)/2 = 1.618033989 and an angle based on this will have size arcsec(1.618033989) = 51° 50'. Now the sides of the Great Pyramid rise at an angle of 51° 52'. Is this a coincidence? F Röber, in 1855, was the first to argue that the golden number had been used in the construction of the pyramids. Many authors have followed Röber, or produced even more elaborate versions of how and the golden number have been utilised by the Egyptians. The authors of [23], however, suggest reasons for the occurrence of many of the nice numbers, in particular numbers close to powers of the golden number, as arising from the building techniques used rather than being deliberate decisions of the architects. Arguments of this type have appeared more frequently in recent years.
Even if deep mathematical ideas went into the construction of the pyramids, I think that Ifrah makes a useful contribution to this debate in [4] when he writes:-
I once knew a professor of mathematics who ... tried to persuade his students that abstract geometry was historically prior to its practical applications, and that the pyramids and buildings of ancient Egypt "proved" that their architects were highly sophisticated mathematicians. But the first gardener in history to lay out a perfect ellipse with three stakes and a length of string certainly held no degree in the theory of cones! Nor did Egyptian architects have anything more than simple devices -- "tricks", "knacks" and methods of an entirely empirical kind, no doubt discovered by trial and error -- for laying out their ground plans.The first definite mathematical influence on architecture we mention is that of Pythagoras. Now for Pythagoras and the Pythagoreans, number took on a religious significance. The Pythagorean belief that "all things are numbers" clearly had great significance for architecture so let us consider for a moment what this means. Taken at face value it might seem quite a silly idea but in fact it was based on some fundamental truths. Pythagoras saw the connection between music and numbers and clearly understood how the note produced by a string related to its length. He established the ratios of the sequence of notes in a scale still used in Western music. By conducting experiments with a stretched string he discovered the significance of dividing it into ratios determined by small integers. The discovery that beautiful harmonious sounds depended on ratios of small integers led to architects designing buildings using ratios of small integers. This led to the use of a module, a basic unit of length for the building, where the dimensions were now small integer multiples of the basic length.
Numbers for Pythagoras also had geometrical properties. The Pythagoreans spoke of square numbers, oblong numbers, triangular numbers etc. Geometry was the study of shapes and shapes were determined by numbers. But more than this, the Pythagoreans developed a notion of aesthetics based on proportion. In addition geometrical regularity expressed beauty and harmony and this was applied to architecture with the use of symmetry. Now symmetry to a mathematician today suggests an underlying action of a group on a basic configuration, but it is important to realise that the word comes from the ancient Greek architectural term "symmetria" which indicated the repetition of shapes and ratios from the smallest parts of a building to the whole structure. It should now be clear what the belief that "all things are numbers" meant to the Pythagoreans and how this was to influence ancient Greek architecture.
Let us look briefly at the dimensions of the Parthenon to see how the lengths conform to the mathematical principles of proportion of the Pythagoreans. In 480 BC the Acropolis in Athens was totally destroyed by the Persians in the Second Persian War. To understand the timescale, let us note that this was about the time of the death of Pythagoras. After the Greek victory over the Persian at Salamis and Plataea the Greeks did not begin the reconstruction of the city of Athens for several years. Only after the Greek states ended their fighting in the Five Years' Truce of 451 BC did the conditions exist to encourage reconstruction. Pericles, the Head of State in Athens, set about rebuilding the temples of the Parthenon in 447 BC. The architects Ictinus and Callicrates were employed, as was the sculptor Phidias.
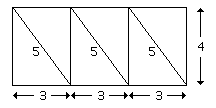
Berger, in [11], makes a study of the way that the Pythagorean ideas of ratios of small numbers were used in the construction of the Temple of Athena Parthenos. The ratio 2 : 3 and its square 4 : 9 were fundamental to the construction. A basic rectangle of sides 4 : 9 was constructed from three rectangles of sides 3 and 4 with diagonal 5. This form of construction also meant that the 3 : 4 : 5 Pythagorean triangle could be used to good effect to ensure that right angles in the building were accurately determined.
The length of the Temple is 69.5 m, its width is 30.88 m and the height at the cornice is 13.72 m. To a fairly high degree of accuracy this means that the ratio width : length = 4 : 9 while also the ratio height : width = 4 : 9. Berger took the greatest common denominator of these measurements to arrive at the ratios
height : width : length = 16 : 36 : 81
which gives a basic module of length 0.858 m. Then the length of the Temple is 92 modules, its width is 62 modules and its height is 42 modules. The module length is used throughout, for example the overall height of the Temple is 21 modules, and the columns are 12 modules high. The naos, which in Greek temples is the inner area containing the statue of the god, is 21.44 m wide and 48.3 m long which again is in the ratio 4 : 9. Berger notes the amazing fact that the columns are 1.905 m in diameter and the distance between their axes is 4.293 m, again the ratio of 4 : 9 is being used.
We mentioned above that F Röber believed that the Egyptians had used the golden number in their construction of the pyramids. In the same work of 1855 he also argued that the golden number was used in the construction of the Temple of Athena on the Parthenon. Perhaps this work was very persuasive, or perhaps it presented a romantic idea which people wanted to believe. Whatever the reason, it appears as essentially an accepted fact today by most people that indeed the buildings of the Parthenon achieved their undoubted exceptional beauty through the use of the golden number. There appears little hard evidence to support this view, while Berger's 4 : 9 theory, on the other hand, appears well established.
Plato was much influenced by the ideas of Pythagoras. Plato's theory of ideas makes meaning and concepts as fundamental and real, while the physical realisation of these ideas was not real and of lesser importance. For example the idea of a flower is real and permanent while the physical examples of flowers are only seen as apparent and temporary. Although buildings are not permanent, Plato saw that they were long lasting and therefore more beautiful to him than flowers. He saw mathematics as providing the most fundamental of all ideas and therefore buildings should be designed on mathematical principles. Plato writes in Philebus:-
What I understand here by beauty ... is not what the common man generally understands by this term as, for example the beauty of living things and their representation. On the contrary, it is sometimes rectilinear ... and circular, with the surfaces of solid bodies composed by means of the compasses, the chord, and the set square. For these forms are not, like the others, beautiful under certain conditions; they are always beautiful in themselves.We are fortunate to know quite a bit about the mathematical methods of ancient architecture through the work De architectura Ⓣ by Vitruvius. This is a Latin work on architecture in ten books, dedicated to Octavianus, the adopted son of Julius Caesar, shortly before 27 BC. Vitruvius was himself an architect and engineer, being in charge of building projects in Rome. The ten books are as follows:
- Principles of architectural.
- History of architecture, and architectural materials.
- Ionic temples.
- Doric and Corinthian temples.
- Public buildings, theatres, music, baths, and harbours.
- Town and country houses.
- Interior decoration.
- Water supply.
- Dials and clocks.
- Mechanical engineering with military applications.
It is interesting, particularly given the details above on how the Temple of Athena on the Parthenon was constructed, to look at what Vitruvius says in Book 3 on designing temples. The book begins with an essay on symmetry and then describes the use of symmetry and proportion in the design of temples. For Vitruvius the proportions of the human body were fundamental in achieving beauty and he says that the proportions of the temple should follow these human proportions. He suggests that the circle and the square are perfect figures for generating architectural designs because they approximate the geometry of the spread-eagled human body. There is a religious significance here, since Vitruvius believed that the human body was made in the image of a god and was therefore perfect. Of course many have argued that the golden number can be found in the proportions of the human body so it may be that the evidence found today for the golden number in ancient Greek temples is explained by its relation to human proportions.
One of the remarkable parts of De architectura Ⓣ is Book 5 where Vitruvius discusses acoustics. Sarton writes [6]:-
Vitruvius explains sound as a displacement of air in waves which he compares with the waves that can be observed on the water's surface when a stone is thrown into a pond. What is more remarkable was Vitruvius' application of the wave theory to architectural acoustics. The wave theory of sound was Greek, its application to the acoustics of a hall typically Roman. ... Vitruvius analyzes the acoustics of a theatre and the phenomena that may spoil it, which we call interference, reverberation, echo.The mathematical content of Book 10 is also interesting. In it Vitruvius describes [6]:-
... hoisting machines, engines for raising water, water wheels and water mills, water screws, Ctesibios's pump, water organs, odometers, and he passes from peace engines to war ones, catapults or scorpiones, ballistae, stringing and tuning of catapults, siege engines, tortoises for filling ditches, Hegetor' s ram and tortoise ...Before we leave Vitruvius's De architectura Ⓣ it is worth noting that, although today we see Vitruvius more as a practical man rather than as a scholar, nevertheless Cardan included him in his list of the twelve leading thinkers of all time.
In Europe there was little progress in mathematics and architecture until the 14th and 15th Centuries. Architecture was modelled on the teachings of Vitruvius and on the classical architecture which was still plentiful, particularly in Greece and Italy. The next person we want to mention is Brunelleschi who was trained as a goldsmith. There were really no professional architects at this time and Brunelleschi learnt his skills in architecture by visiting Rome:-
He made drawings of a great many ancient buildings, including baths, basilicas, amphitheatres, and temples, particularly studying the construction of architectural elements, such as vaults and cupolas. The object of his architectural researches, however, was not to learn to reproduce Roman architecture, but to enrich the architecture of his own time and to perfect his engineering skills.Brunelleschi made one of the most important advances with his discovery of the principles of linear perspective. Classical scholars had understood some of the principles of perspective but no text seems to have been written on the topic. We think of an understanding of perspective as being essential for a realistic two dimensional representation of a three dimensional scene when painting on a canvass. However Brunelleschi's understanding of perspective was used in his design of buildings as he created his designs to ensure that the visual effect he wanted was visible from all positions of the observer. Following the rules of proportion and symmetry of the ancients was important to Brunelleschi but he wanted these mathematical principles of beauty to be those seen by all observers. In some sense he was trying to achieve a certain invariance of proportion, independent of the angle of view, and to ensure that it was the apparent proportion which was right rather than the actual proportion. Argan writes [1]:-
Perspective neither uncovers, creates, nor invents space. Rather, it is an essentially critical method or process that can be applied to the spacial data of architecture, reducing it to proportion or to reason. The Platonic influence predominates over Aristotelianism, in the synthesis of longitudinal and central diagrams into a perspective of contemplation, a perspective that leads theoretically to a single point.Many of the famous mathematicians from the time of Brunelleschi made contributions to architecture. Alberti wrote a text on the topic, as well being the author of an important text on perspective in which he wrote down Brunelleschi's brilliant discoveries for the first time. He was one of a number of mathematicians to develop a general theory of proportion which, of course, was motivated by his architectural studies.
Although the name of Leonardo da Vinci makes one think of his stunning paintings rather than mathematics, in fact he was fascinated by mathematics. Architecture was another of his specialities and he learnt about it, in particular the mathematical principles behind it, from studying Alberti's texts. He was a man of wide ranging abilities and interests and, at one stage in his career, earned his living advising the Duke of Milan on architecture, fortifications and military matters. He was also considered as a hydraulic and mechanical engineer. He also worked for Cesare Borgia as a military architect and general engineer. Later the French King Francis I appointed him first painter, architect, and mechanic to the King.
Another mathematician from Renaissance times was Bombelli who was taught by Pier Francesco Clementi, himself an engineer and architect. With this training Bombelli was soon working himself as both engineer and architect employing his mathematical skills both in his work and in his deep investigation of complex numbers. Another to combine his skills in both mathematics and architecture was Bramer who was employed directing constructions of fortifications and castles. He published a work on the calculation of sines, prompted by the practical work in which he was involved. He followed Alberti (1435), Dürer (1525) and Bürgi (1604) when in 1630 he constructed a mechanical device that enabled one to draw accurate geometric perspective.
La Faille was a contemporary of Bramer who taught mathematics and military engineering. He worked as an architect advising on fortifications and he wrote an architectural treatise as well as important works on mechanics. Later in the 17th Century lived the English architect Wren, in many ways the best known architect in English history. A well rounded scientist, he solved a number of important mathematical problems before taking up architecture as a profession. Although he is better known as an architect than as a mathematician he was considered one of the leading mathematicians of his day by Newton. It was clear that Wren saw mathematics as being a subject which had applications to a wide variety of scientific disciplines and his mathematical skills played an important role in his architectural achievements. One of the architects with whom he worked, Robert Hooke, is better known as a mathematician than as an architect. Again that mathematics and architecture were closely related disciplines was considered natural at this time.
Another 17th Century mathematician was La Hire whose interests geometry arose from his study of architecture. In 1687 he was appointed to the chair of architecture at the Académie Royale. His interest in geometry arose from his study of perspective and he went on to make important contributions to conic sections. In the 18th century Poleni made contributions to hydraulics, physics, astronomy and archaeology. He held university chairs in astronomy, physics and mathematics as well as working as an architect.
The nineteenth century saw a change of attitude which led to a separation in people's minds of the scientific and the artistic. From this period the roles of mathematicians and architects were seen as distinct in a way that did not happen in say the seventeenth century. This is not to say that the connections between mathematics and architecture vanished, just that the scientific and artistic aspects were seen as complementary skills not to be found in the same person. Of course there were still those who did excel in mathematics and architecture; it was only perceptions which changed. An example of a person who excelled in architecture and mathematics was Aronhold who taught at the Royal Academy of Architecture at Berlin from 1851. Aronhold was appointed professor at the Royal Academy of Architecture in 1863. He made outstanding contributions to geometry.
Others from this period who combined the two skills include Brioschi and Wiener. From 1852 to 1861 Brioschi was professor of applied mathematics at the University of Pavia. There he taught mechanics, architecture and astronomy. Wiener studied engineering and architecture at the University of Giessen from 1843 to 1847. With this training he went on to become a teacher of physics, mechanics, hydraulics and descriptive geometry at the Technische Hochschule in Darmstadt.
There are a number of late 19th Century, and 20th Century mathematician who began their careers as architects before turning to mathematics, for example the Frenchman Drach and the American Wilks. Drach worked as an architect before turning to mathematics. Wilks studied architecture at North Texas State Teachers College. He received a B.A. in architecture in 1926. However his eyesight was not too good, and he feared that this would be a handicap if he pursued architecture as a profession so he decided on a career in mathematics.
Two unique talents from the 20th Century were Escher and Buckminster Fuller. Escher was never a mathematician, despite his fascination with the subject and the deep mathematical ideas which underlay his art. He trained at the School of Architecture and Decorative Arts in Haarlem and only at age 21 did he give up architecture in favour of art. Buckminster Fuller was an engineer, mathematician and architect who applied geometric principles to design a totally new concept in buildings in the second half of the 20th Century. He made an art out of structural purity, using simple geometric forms for aesthetic as well as functional purposes.
References (show)
- G C Argan, Brunelleschi (Milan, 1955).
- M S Bulatov, Geometric harmonization in Central Asian architecture in the 9th-15th centuries, Historical-theoretic research Nauka (Moscow, 1988).
- J V Field, The invention of infinity : Mathematics and art in the Renaissance (Oxford, 1997).
- G Ifrah, The Universal History of Numbers (London, 1998).
- P Radelet-de Grave and E Benvenuto, Entre mécanique et architecture (Basel, 1995).
- G Sarton, Hellenistic science and culture in the last three centuries B.C. (New York, 1993).
- K Williams (ed.), Nexus III : architecture and mathematics, Ferrara, June 4-7, 2000 (Pisa, 2000).
- K N Afanas'ev, Ancient metrology and architecture (Russian), Istor.-Astronom. Issled. No. 20 (1988), 194-201.
- D J Bassegoda Nonell, Line geometry and architecture (Spanish), Mem. Real Acad. Cienc. Artes Barcelona 48 (10) (1989), 23.
- J A Bennett, Christopher Wren : astronomy, architecture, and the mathematical sciences, J. Hist. Astronom. 6 (3) (1975), 149-184.
- E Berger, Bauwerk und Plastik des Parthenon, in Antike Kunst (Basel, 1980).
- F Calio and Marchetti, Generation of architectural forms through linear algebra, in Nexus III : architecture and mathematics, Ferrara, June 4-7, 2000 (Pisa, 2000), 9-22.
- F Camerota, Architecture and science in baroque Rome : The mathematical ornaments of Villa Pamphilj, Nuncius Ann. Storia Sci. 15 (2) (2000), 589-638.
- A Capanna, Conoids and hyperbolic paraboloids in Le Corbusier's Philips Pavilion, in Nexus III : architecture and mathematics, Ferrara, June 4-7, 2000 (Pisa, 2000), 35-44.
- Y Dold-Samplonius, Calculation of arches and domes in 15th century Samarkand, in Nexus III : architecture and mathematics, Ferrara, June 4-7, 2000 (Pisa, 2000), 45-55.
- A Fiocca, Books on architecture and mathematics in the library of Giovan Battista Aleotti (Italian), Boll. Storia Sci. Mat. 15 (1) (1995), 85-132.
- R Fletcher, Golden proportions in a great house : Palladio's Villa Emo, in Nexus III : architecture and mathematics, Ferrara, June 4-7, 2000 (Pisa, 2000), 73-85.
- H Groemer, The symmetries of frieze ornaments in Maya architecture, Osterreich. Akad. Wiss. Math.-Natur. Kl. Sitzungsber. II 203 (1994), 101-116.
- D A King, The orientation of medieval Islamic religious architecture and cities, J. Hist. Astronom. 26 (3) (1995), 253-274.
- P Lipnik, Architecture de Mgr G Lemaître en arithmétique, Rev. Questions Sci. 168 (2) (1997), 161-178.
- L Mancini Proia and M Menghini, From polycentric ovals to ellipses in Baroque architecture (a possible conceptual derivation from astronomy) (Italian), Atti Accad. Sci. Torino Cl. Sci. Fis. Mat. Natur. 118 (5-6) (1984), 325-338.
- G Necipoglu, The Topkapi scroll - geometry and ornament in Islamic architecture, Topkapi Palace Museum Library MS H. 1956 (Santa Monica, CA, 1995).
- L Pepe, Architecture and mathematics in Ferrara from the thirteenth to the eighteenth centuries, Nexus III : architecture and mathematics, Ferrara, 2000 (Pisa, 2000), 87-104.
- M A Reynolds, A new geometric analysis of the Pazzi Chapel in Santa Croce, Florence, in Nexus III : architecture and mathematics, Ferrara, June 4-7, 2000 (Pisa, 2000), 105-121.
- G Robins and C C D Shute, Mathematical bases of ancient Egyptian architecture and graphic art, Historia Math. 12 (2) (1985), 107-122.
- M Rubin, Architecture and geometry, Structural Topology No. 1 (1979), 13-25; 73.
- Z Sagdic, Ottoman architecture: relationships between architectural design and mathematics in architect Sinan's works, in Nexus III : architecture and mathematics, Ferrara, June 4-7, 2000 (Pisa, 2000), 123-132.
- N A Salingaros, Architecture, Patterns, and Mathematics, Nexus Network Journal 1 (2) (April 1999).
- M Spigaroli, Pulchritudo sive proportio : Architecture and mathematics in the gothic of the mendicants, Nexus Netw. J. 1 (3) (1999), 9 pp. (electronic).
- S R Wassell, Art and mathematics before the Quattrocento : a context for understanding Renaissance architecture, in Nexus III : architecture and mathematics, Ferrara, June 4-7, 2000 (Pisa, 2000), 157-168.
- O H Zhao, The effect of Prospettiva de' pittori, e architetti by Andrea Pozzo (b. Trent, 1642, d. Vienna, 1709) on Chinese painting, drawing and architecture, in Proceedings of the Third International Conference on Engineering Graphics and Descriptive Geometry 2, Vienna, 1988 (Vienna, 1988), 323-329.
Written by J J O'Connor and E F Robertson
Last Update February 2002
Last Update February 2002