MacTutor
Kepler's Planetary Laws
1. Introduction
This account of Kepler's mathematical astronomy may well challenge some cherished and long-held beliefs, since most of what has been written about Kepler has either been based on secondary or tertiary sources, or has concentrated on his astronomical background and techniques. But Kepler was a highly-talented geometer, and until now has there been no investigation of his work (derived from the original Latin) which has highlighted the mathematical aspect of his brilliance. While analysis of his success has led to some unexpected conclusions, the present overview has been endorsed in detail by articles published in learned historical journals. These are listed on the web site mentioned at the end; they also contain references to traditional accounts which are becoming superseded.
The greatest achievement of Kepler (1571-1630) was his discovery of the laws of planetary motion. There were such three laws, but here we shall deal only with the first two - those that govern the motion of an individual planet. These are found in Astronomia Nova Ⓣ 1609, underpinned by important work in Epitome Ⓣ Book V (1621). The laws are:
Kepler's principal aim was to find a solution that would satisfy observations - and in that respect he possessed the outlook of a modern scientist. Moreover, Renaissance scientists considered it their duty to reveal the way in which Nature worked by explaining the observed outcome by the simplest means available. Strongly influenced both by Plato and by his underlying belief in God, Kepler believed more intensely than his contemporaries in the power of mathematics to expose the order in the universe that lay behind apparent complication, and he applied this criterion of simplicity with great effect in his astronomy.
There is much additional information, both on the circumstances of Kepler's life, and the context in which he worked, in the MacTutor biography. This will provide useful background to the present detailed account of his astronomical work.
2. Observational background
Kepler originally investigated the orbit of Mars because that was the task allocated to him by Tycho Brahe (1546-1601), when Kepler joined him in Prague around 1600. In their day - and indeed until comparatively recently - the aim of astronomers was to achieve accurate observations of angles, simply because no other feature could be measured directly. Tycho had amassed a vast store of observations extending over 30 years; these are probably the most accurate that would ever be made with the naked eye, since Galileo (1564-1642) had introduced the telescope into astronomy soon afterwards (in 1610). Tycho developed, refined and cross-checked his instruments and sometimes attained an accuracy of 2' (which is approximately the breadth of a hair held at arm's length).
It so happens that Mars is the only planet whose noncircularity can be detected without a telescope, and its observability was favoured by four factors:
Since Greek times, the accepted description of the planetary system had been a geometrical one, known as the Ptolemaic theory (a geocentric configuration), which supposed that the Earth was fixed at the centre of the universe, with the Moon, the Sun, and the five known (naked-eye) planets revolving round it. Geocentricity was obviously in accordance with the evidence of the senses - as well as being the only arrangement acceptable to the Church - by contrast with the heliocentric configuration, which was proposed by Copernicus (1473-1543). Kepler was introduced to Copernicanism as a student at the University of Tübingen by his teacher, Michael Maestlin (1550-1631). Though his contemporaries were in general slow to recognize any advantages in this new idea, Kepler adopted the Copernican theory enthusiastically, because of its greater simplicity - which allowed him to abandon the set of (five) large and cumbersome epicycles that occurred in the Ptolemaic theory (they accounted for what we now recognize as the actual motion of the Earth). In fact, Kepler gave Copernican theory a new, mathematical precision by specifying two fundamental tenets that were consistent with his conviction that the Sun was metaphorically the place of God:
4. Reduction of observations leading to idealization
In the earlier chapters of Astronomia Nova Ⓣ Kepler embarked on a programme of 'reducing the observations' (this term means removing, as far as possible, all effects due to the observer's position in time and space). He found the heavy calculations, and the necessary checking, 'mechanical and tedious', as he remarked later: he did not have the benefit of logarithms, which were not invented until 1614, by Napier (1550-1617). Kepler carried out the reduction to heliocentricity, and further simplifying procedures, in a series of steps:
5. Essential orthogonality of Euclid's geometry
In Kepler's day modern algebraic notation and techniques were just being developed, but for his approach to astronomy Kepler depended exclusively on the traditional geometry of Euclid in which he had been trained at the University of Tübingen, as part of the standard preparation for the ministry. (This was originally Kepler's intended profession, and all his life he remained a devout, though somewhat unorthodox, Lutheran). Euclid's Elements rigorously laid down (in the first three Postulates) that the only means of construction permitted were the straightedge (an unmarked ruler) and compasses. Thus, the distinguishing feature of the geometry of Elements was that it relied on straight lines and circles alone. These were then combined in one of Euclid's earliest propositions concerning circles, which stated in effect that where the diameter of a circle meets its circumference a right angle will occur. It is well-known that a pair of (mathematically-defined) directed quantities are mutually independent if and only if they are at right angles: using Euclid's term 'orthogonal' for mutually perpendicular (it was defined in Elements Book I), this will be named the Principle of Orthogonal Independence; it will, with hindsight, justify our separate treatment of the path and the time-measure. (Moreover, the same principle is invoked in relation to planetary motion when Kepler based his investigation on what Aristotle had specified as the only two simple motions, circular and rectilinear, discussed in Section 9.) This principle has far-reaching ramifications, as we will demonstrate in connection with the complementary pairings that recur in Kepler's mature work in Epitome Ⓣ Book V (1621) - where the term 'complementary' is used in the everyday sense that the pair complete one another, and also with the mathematical connotation of being at right angles. Application of the principle gives rise to an enormous leap in simplicity, since it is intuitively obvious that it will be easier to treat each one of a pair of components separately than to work with the resultant produced by taking them in combination. For Kepler, simplicity was the hallmark of his treatment, and contributed overwhelmingly to his success.
Kepler always showed the greatest respect for his Greek predecessors, and read their works thoroughly, selecting material that he could incorporate into his new astronomical synthesis. Apart from frequent application of the trigonometrical propositions of Ptolemy (fl. 129-141 AD), Kepler made use of precisely three propositions from the work of Archimedes; one of these was vital in supplying the geometrical backing for Section 6 (the other two - one cited in Section 7, one in Section 11 - were concerned with an innovative approach to 'infinitesimal' considerations which went well beyond traditional geometry). However, it will come as a surprise to some readers to find that Kepler did not rely on Apollonius anywhere in his astronomical work. Sometime in the years 1594-1604, Kepler studied the Conics of Apollonius, and expressed great admiration for it, citing it throughout his optical and stereometrical work - yet he never referred to any of its propositions in connection with his astronomy. This is because Conics is expressed in terms of an oblique (non-orthogonal) frame of reference (coordinate-system), which Kepler implicitly rejected as inappropriate for the study of astronomy (nor did he need any of its propositions, as we confirm in Section 6). Meanwhile we reiterate Kepler's belief that Euclid's Elements encapsulated the only geometry that could properly be applied to the heavens, which after all was the realm of God. He labelled any other treatment 'ageometrical' - which, in his mind, was akin to heretical.
6. Constructing the path
In spite of his splendid inheritance from Tycho, Kepler knew that no amount of empirical observations, however numerous, could give him the theoretical structure he required. Therefore, when he had compensated for the observational uncertainties as far as possible, Kepler switched to a geometrical investigation - see Figure (1). He began by assuming a fixed/known line of apsides CD, on which lies the fixed point A (the position of the Sun) at a known 'eccentric' distance AB (all previously determined from Tycho's observations), where B is the midpoint of CD. (From now on, as a convenience, we shall use the algebraic notation BC = BD = , AB = , even though it is an anachronism.)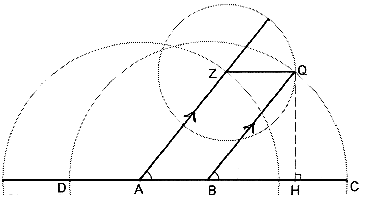
Figure 1
Kepler started from the initial framework illustrated in Figure (1), which could be described as standard Ptolemaic, except that Kepler automatically transposed it from geocentric to heliocentric mode. He adopted the traditional mechanism of deferent, epicycle, and eccentric, being aware, as the Ancients had been, that motion in the circle of radius centred on A, when combined with motion in the epicyclet of radius ZQ = AB = (whose centre Z lies on the deferent), together produce a motion of Q equivalent to a simple motion of Q round the eccentric circle centre B radius . (Mathematicians may like to regard ABQZ as a 'parallelogram of circular motions'.) We shall specify the typical point of any of the three successive orbits proposed by Kepler just as he did - determined by the angle at the centre of the eccentric circle, which we shall denote by β for distinctiveness. (This usage was authenticated by tradition, since in ancient astronomy motions consisted of combinations of rotations which were measured by the angles at the centres of their respective circles.) Then we have corresponding angles from the parallels AZ and BQ, so that:
At the first stage Kepler took Q on the eccentric circle as the typical point and so he tested the eccentric itself as a proposed path. However, he found that this placed the planet too far from the Sun in almost all positions. So he finally rejected the idea that each planet moved in a single circle, and set out to find the actual curve that was the planet's path - naturally, this had to be constructed from a combination of (arcs of) circles by the geometry of Euclid, since Kepler recognized nothing else as appropriate for the heavens.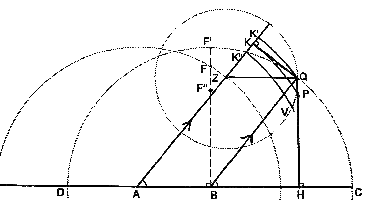
Figure 2
The typical points of the three successive proposed paths are all named, and the separate constructions shown, in Figure (2). It is evident that the structure needed to produce these points already, or potentially, exists in Figure (1) in terms of a chosen value QBC = β. This is significant because - as we will see in Section 7 - the time is also expressed in terms of β, so a common value of β ensures simultaneity. The three-stage procedure that Kepler adopted was to take geometrically-defined points (K', K'', K) along AZ, one at each stage in turn, then with centre A to draw the corresponding circular arc (radius AK', AK'', AK), so that each arc would end at a geometrically-defined point (Q, V, P) respectively. The stages are classified according to the chapters of Astronomia Nova Ⓣ in whch each construction appears: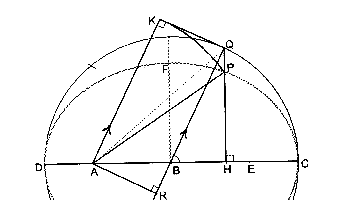
Figure 3
So the resulting radius vector AP that finally satisfied Kepler (in Ch.58) was quantified geometrically from the constructed rectangle AKQR, by applying nothing more than a Euclidean - straightedge-and-compasses - construction, as shown in Figure (3):
[It is expressed in modern terms for reference in the Summary Table at the end: also see the article Planetary motion tackled kinematically.]
However, such a construction had never been invented before and Kepler did not have the slightest idea what curve the above relationship represented. However, he did know that if the curve were an ellipse, the typical point P would satisfy a vital condition that he had come across in the work of Archimedes: On Conoids and Spheroids Prop.4 (where it was stated as if well known even then):
The identification of the curve as an ellipse also depends on a relationship that Kepler established in Ch. 59, Prop. VII, which we express here in modern terms (writing BF = to denote the minor semiaxis), recognizing that will now represent the (focal) eccentricity:
In Astronomia Nova Ⓣ Ch. 59, Prop. XI, Kepler set out a rigorous geometrical proof that the typical point he had constructed satisfied the ratio-property which defines an ellipse. Hence, there can be no suggestion that Kepler merely selected an ellipse and checked it against observations (as many readers may have been told). Because of its importance the proof has been reproduced more than once [2]; though modernized in style, and reordered - to increase its impact - clearly it has not been altered in substance, since it relies on nothing more 'advanced' than Pythagoras' Theorem, and properties of similar triangles. Thus (apart from the use of definition (1) above) the proof is entirely based on cited or implied propositions from Euclid's Elements. Incidentally, this provides additional confirmation of my contention (in Section 5) that Kepler did not rely on the Conics of Apollonius for his discovery of the ellipse - in his astronomy he simply did not need anything so sophisticated.
Kepler set out a rigorous geometrical proof that the typical point he had constructed satisfied the ratio-property which defines an ellipse. Hence, there can be no suggestion that Kepler merely selected an ellipse and checked it against observations (as many readers may have been told). Because of its importance the proof has been reproduced several times [2]; though modernized in style, and reordered - to increase its impact - clearly it has not been altered in substance, since it relies on nothing more 'advanced' than Pythagoras' Theorem, and properties of similar triangles. Thus (apart from the use of relationship (1) above) the proof is entirely based on cited or implied propositions from Euclid's Elements. Incidentally, this provides additional confirmation of my contention (in Section 5) that Kepler did not rely on the Conics of Apollonius for his discovery of the ellipse - in his astronomy he simply did not need anything so sophisticated.
7. Constructing the representation of time
This investigation took place alongside, but independently of, the construction of the path of the planet. From a heliocentric point of view, it is especially easy to be aware that planets move more slowly the further they are from the Sun (and faster when nearer). Thus, as Kepler realized, a connection exists between a small (micro) interval of time and the corresponding distance of the planet from the Sun. Kepler's practical problem in Astronomia Nova Ⓣ, however, was to discover a way of measuring the time taken to reach the typical position (P) of the planet at an intermediate point of the orbit. Initially, he suggested that this (macro) time (the sum of the micro intervals of time) could be represented geometrically by the sum of all the corresponding distances from the Sun. In Ch.40, at the first of the three stages set out in Section 6, Kepler put this into practice, by citing Archimedes, Measurement of a Circle, Prop.3, to justify him in taking a sum of distances to be equivalent to the area of a sector of a circle.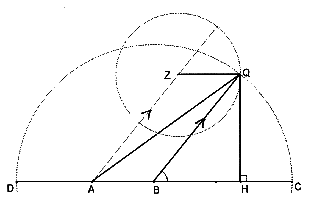
Figure 4
Next, Kepler extended that proposition, and took the distance-sum from the eccentric point (A, the position of the Sun) to be (approximately) proportional to the area of the eccentric sector (the area QAC, shown in Figure (4)). Then he demonstrated geometrically how to find the area of such a sector (devising alternative ways of splitting up the area as he required them):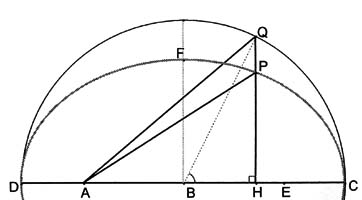
Figure 5
Using these two results, again from Figure (5), Kepler deduced:
[In modern algebraic terms it is easy to establish, from Figure (5), that:
The above relationship, expressing Time ∝ Area in its most precise formulation, is nowadays known as Law II. It appears for reference in the Summary Table at the end.
8. Kepler's subsequent justification of the two laws
This is where the accounts of Kepler's work generally stop - but Kepler achieved much more. Firstly, between 1609 and 1618, he satisfied himself that the orbit of each of the six primary planets was an ellipse with the Sun at one focus. He went on to tackle the problem of the motions of planets, and their causes, in Epitome Astronomiae Copernicanae Ⓣ. This consists of seven books, though only Book V (1621), supported in places by Book IV (1620), contains the really innovative work. Despite the title, it epitomizes Keplerian, rather than Copernican astronomy. And further confirmation of the motions is given in Harmonice Mundi Ⓣ, 1618 Book V, Chapter 3, where there are some quantified references to a single planet, in addition to the main discussion which involves the planetary system. Unfortunately, Kepler's investigation of the motions was little appreciated by his contemporaries, and largely ignored subsequently. However, the overall success of his theory was confirmed in practice through the Rudolphine Tables (1627) - which, unlike other astronomical tables, remained observationally accurate and useful for many decades: see Kepler. These tables were calculated in terms of β, which can now be identified as the auxiliary angle of the ellipse. The mathematical treatment carried out in Planetary motion tackled kinematically demonstrates that this angle is the uniquely appropriate foundation for a structure which is simple because it depends on orthogonality and therefore is the only workable basis for Kepler's astronomy.
9. Essential orthogonality of the components of motion and their associated causes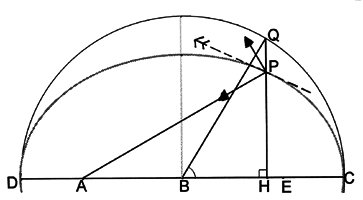
Figure 6
In De Caelo Ⓣ I, 3, Aristotle had declared that there were only two simple motions, circular and linear. Accordingly, on this authority, Kepler was able to match each one of the pair of results (the curve, and the independently-determined representation of time) that he had discovered in Astronomia Nova Ⓣ, to one of these mutually perpendicular components of motion. So this introduces another instance of the Principle of Orthogonal Independence (in fact dated earlier than Euclid). These components are listed in the Summary Table at the end for reference, and illustrated in Figure (6) by solid arrows:
Neither was Kepler's approach to the problem of causes of motion in any mathematical sense an anticipation of the work of Newton (despite the views of some previous commentators); it was, by contrast, governed by his background in the Aristotelian tradition. Though this Aristotelian 'physics' was becoming outdated even in Kepler's day, people still believed that an object would not move unless there was a 'force' or cause of motion to make it do so. Also, this 'force' had to act by contact; and, the object would then move only in the direction of the 'force', while the amount of 'force' was responsible for the amount of motion produced. Kepler could never have supposed that the Sun could exert an attractive force because that concept did not exist in Aristotelian terms.
10. The Sun's rotation: the cause of transradial motion
We will deal first with the cause of the transradial motion because the revolution of the planets round the Sun is the most outstanding feature of a heliocentric universe, and requires a universal cause. Kepler accounted for that motion by inventing the rotation of the Sun on its axis. He suggested this a few years before the rotation was actually established, c.1610, from observations of sunspots by Galileo, Scheiner (a minor contemporary astronomer), and independently by Harriot (c.1560-1621). Thus, Kepler envisaged that the rays emitted by the rotating Sun would 'hit' or impel each planet continuously round in a circle. Naturally, he expected that this impulsion would be less when the planet was further from the Sun, so he reasonably supposed that the action of the rays would vary inverse-linearly (that is, weaken) with distance. Amazingly, the formulation of this cause then exactly agrees with the evaluation of the transradial motion set out in the Summary Table at the end, as is confirmed by the modern treatment in Planetary motion tackled kinematically.
11. Magnetism: the cause of radial motion
To account for radial motion, Kepler obviously needed a cause that would be individual to each planet, because every planetary ellipse is a different shape. He selected magnetism, having come across a recently-published book, De Magnete Ⓣ, 1600 by Gilbert (1544-1603), which stated that the Earth should be regarded as a giant magnet. Because of his Copernican convictions, Kepler extended this idea to suppose that every planet possessed magnetism, and contained a set of 'fibres' fixed within its body which could be activated by the Sun's magnetism; and he further supposed that each set of fibres possessed a unique potential magnetic 'strength' that could be associated with the individual eccentricity of the particular planetary path. Unfortunately the way this cause was supposed to function cannot be associated with action at a distance (because this was a nonAristotelian concept). Thus it is not correct - nor is it meaningful - to interpret Kepler's magnetism as a 'force', either in an Aristotelean or in a modern context. The radial motion itself was evaluated by taking a small variation (an increment) of the distance from the Sun with respect to a small change in the auxiliary angle: see Summary Table at the end, confirmed by the modern treatment in Planetary motion tackled kinematically. Ultimately the cause provided its own justification - because the radial motion it produced is sound in mathematical terms.
12. The associated pair of orthogonal causes
Kepler was the first to introduce the concept of causation into astronomy, and in accordance with his Copernican convictions, he naturally believed that the Sun was the generator of all causes. Moreover, it seemed common sense to suppose that the Sun could only act (or activate) continuously either in a radial direction or circularly round itself, and this consideration, for Kepler, determined the direction of the causes available and limited their number to two. Thus the causes (as well as the motions and the constituents of the orbit) were also subject to the operation of the Principle of Orthogonal Independence.
Hence, each of the pair of perpendicular component motions illustrated in Figure (6) can be matched to its own distinct cause, as indicated in the Summary Table at the end, in accordance with the Principle of Economy (another relic of Aristotle) - one cause per motion. We summarize Kepler's final suppositions:
13. Conclusion: the criterion of simplicity
Kepler was able to formulate a complete account of planetary motion using only elementary geometry, and accordingly we will highlight the two overriding reasons for his achievement, putting them in a historical context. They are both new to Keplerian analysis.
This account of Kepler's mathematical astronomy may well challenge some cherished and long-held beliefs, since most of what has been written about Kepler has either been based on secondary or tertiary sources, or has concentrated on his astronomical background and techniques. But Kepler was a highly-talented geometer, and until now has there been no investigation of his work (derived from the original Latin) which has highlighted the mathematical aspect of his brilliance. While analysis of his success has led to some unexpected conclusions, the present overview has been endorsed in detail by articles published in learned historical journals. These are listed on the web site mentioned at the end; they also contain references to traditional accounts which are becoming superseded.
The greatest achievement of Kepler (1571-1630) was his discovery of the laws of planetary motion. There were such three laws, but here we shall deal only with the first two - those that govern the motion of an individual planet. These are found in Astronomia Nova Ⓣ 1609, underpinned by important work in Epitome Ⓣ Book V (1621). The laws are:
- Law I (the Ellipse Law) - the curve or path of a planet is an ellipse whose radius vector is measured from the Sun which is fixed at one focus.
- Law II (the Area Law) - the time taken by a planet to reach a particular position is represented by the area swept out by the radius vector drawn from the fixed Sun.
Kepler's principal aim was to find a solution that would satisfy observations - and in that respect he possessed the outlook of a modern scientist. Moreover, Renaissance scientists considered it their duty to reveal the way in which Nature worked by explaining the observed outcome by the simplest means available. Strongly influenced both by Plato and by his underlying belief in God, Kepler believed more intensely than his contemporaries in the power of mathematics to expose the order in the universe that lay behind apparent complication, and he applied this criterion of simplicity with great effect in his astronomy.
There is much additional information, both on the circumstances of Kepler's life, and the context in which he worked, in the MacTutor biography. This will provide useful background to the present detailed account of his astronomical work.
2. Observational background
Kepler originally investigated the orbit of Mars because that was the task allocated to him by Tycho Brahe (1546-1601), when Kepler joined him in Prague around 1600. In their day - and indeed until comparatively recently - the aim of astronomers was to achieve accurate observations of angles, simply because no other feature could be measured directly. Tycho had amassed a vast store of observations extending over 30 years; these are probably the most accurate that would ever be made with the naked eye, since Galileo (1564-1642) had introduced the telescope into astronomy soon afterwards (in 1610). Tycho developed, refined and cross-checked his instruments and sometimes attained an accuracy of 2' (which is approximately the breadth of a hair held at arm's length).
It so happens that Mars is the only planet whose noncircularity can be detected without a telescope, and its observability was favoured by four factors:
- it is an outer planet (and therefore it is seldom viewed close to the Sun);
- the noncircularity of its path is the greatest of the outer planets;
- it is the nearest to the Earth of the outer planets (so changes in position appear larger);
- it is the nearest to the Sun of the outer planets (and therefore it makes more frequent circuits, producing more observations).
Since Greek times, the accepted description of the planetary system had been a geometrical one, known as the Ptolemaic theory (a geocentric configuration), which supposed that the Earth was fixed at the centre of the universe, with the Moon, the Sun, and the five known (naked-eye) planets revolving round it. Geocentricity was obviously in accordance with the evidence of the senses - as well as being the only arrangement acceptable to the Church - by contrast with the heliocentric configuration, which was proposed by Copernicus (1473-1543). Kepler was introduced to Copernicanism as a student at the University of Tübingen by his teacher, Michael Maestlin (1550-1631). Though his contemporaries were in general slow to recognize any advantages in this new idea, Kepler adopted the Copernican theory enthusiastically, because of its greater simplicity - which allowed him to abandon the set of (five) large and cumbersome epicycles that occurred in the Ptolemaic theory (they accounted for what we now recognize as the actual motion of the Earth). In fact, Kepler gave Copernican theory a new, mathematical precision by specifying two fundamental tenets that were consistent with his conviction that the Sun was metaphorically the place of God:
- The Sun is the fixed hub of the universe. This was bounded by the fixed stars and consisted of the six known (primary) planets, now including the Earth, with the Moon downgraded as its satellite (a term coined by Kepler himself);
- The Sun is responsible for all celestial motion.
4. Reduction of observations leading to idealization
In the earlier chapters of Astronomia Nova Ⓣ Kepler embarked on a programme of 'reducing the observations' (this term means removing, as far as possible, all effects due to the observer's position in time and space). He found the heavy calculations, and the necessary checking, 'mechanical and tedious', as he remarked later: he did not have the benefit of logarithms, which were not invented until 1614, by Napier (1550-1617). Kepler carried out the reduction to heliocentricity, and further simplifying procedures, in a series of steps:
- In order to transpose the observations from a geocentric to a heliocentric basis, he applied triangulation to ensure that each Mars-distance was measured as if from the fixed Sun. Bearing in mind that the observations contained no distance-measurements (as explained in Section 2), this involved expressing all the Mars-Sun distances in terms of the Earth-Sun distance, regarded as a standard unit or 'baseline' (since the path of the Earth is very nearly circular, this approximation happened to be accurate enough for Kepler's purpose);
- He verified that the path of each planet lay in a plane that passed through the Sun;
- He checked that the observations were compatible with the fact that the curve described by the planet possessed a single axis of symmetry - identified as the line of apsides;
- Finally, he tabulated the average values of the secular changes, from knowledge accumulated over many centuries,which accounted for many of the small remaining irregularities. Thus Kepler knew the angular amount he should allow as compensation for them.
5. Essential orthogonality of Euclid's geometry
In Kepler's day modern algebraic notation and techniques were just being developed, but for his approach to astronomy Kepler depended exclusively on the traditional geometry of Euclid in which he had been trained at the University of Tübingen, as part of the standard preparation for the ministry. (This was originally Kepler's intended profession, and all his life he remained a devout, though somewhat unorthodox, Lutheran). Euclid's Elements rigorously laid down (in the first three Postulates) that the only means of construction permitted were the straightedge (an unmarked ruler) and compasses. Thus, the distinguishing feature of the geometry of Elements was that it relied on straight lines and circles alone. These were then combined in one of Euclid's earliest propositions concerning circles, which stated in effect that where the diameter of a circle meets its circumference a right angle will occur. It is well-known that a pair of (mathematically-defined) directed quantities are mutually independent if and only if they are at right angles: using Euclid's term 'orthogonal' for mutually perpendicular (it was defined in Elements Book I), this will be named the Principle of Orthogonal Independence; it will, with hindsight, justify our separate treatment of the path and the time-measure. (Moreover, the same principle is invoked in relation to planetary motion when Kepler based his investigation on what Aristotle had specified as the only two simple motions, circular and rectilinear, discussed in Section 9.) This principle has far-reaching ramifications, as we will demonstrate in connection with the complementary pairings that recur in Kepler's mature work in Epitome Ⓣ Book V (1621) - where the term 'complementary' is used in the everyday sense that the pair complete one another, and also with the mathematical connotation of being at right angles. Application of the principle gives rise to an enormous leap in simplicity, since it is intuitively obvious that it will be easier to treat each one of a pair of components separately than to work with the resultant produced by taking them in combination. For Kepler, simplicity was the hallmark of his treatment, and contributed overwhelmingly to his success.
Kepler always showed the greatest respect for his Greek predecessors, and read their works thoroughly, selecting material that he could incorporate into his new astronomical synthesis. Apart from frequent application of the trigonometrical propositions of Ptolemy (fl. 129-141 AD), Kepler made use of precisely three propositions from the work of Archimedes; one of these was vital in supplying the geometrical backing for Section 6 (the other two - one cited in Section 7, one in Section 11 - were concerned with an innovative approach to 'infinitesimal' considerations which went well beyond traditional geometry). However, it will come as a surprise to some readers to find that Kepler did not rely on Apollonius anywhere in his astronomical work. Sometime in the years 1594-1604, Kepler studied the Conics of Apollonius, and expressed great admiration for it, citing it throughout his optical and stereometrical work - yet he never referred to any of its propositions in connection with his astronomy. This is because Conics is expressed in terms of an oblique (non-orthogonal) frame of reference (coordinate-system), which Kepler implicitly rejected as inappropriate for the study of astronomy (nor did he need any of its propositions, as we confirm in Section 6). Meanwhile we reiterate Kepler's belief that Euclid's Elements encapsulated the only geometry that could properly be applied to the heavens, which after all was the realm of God. He labelled any other treatment 'ageometrical' - which, in his mind, was akin to heretical.
6. Constructing the path
In spite of his splendid inheritance from Tycho, Kepler knew that no amount of empirical observations, however numerous, could give him the theoretical structure he required. Therefore, when he had compensated for the observational uncertainties as far as possible, Kepler switched to a geometrical investigation - see Figure (1). He began by assuming a fixed/known line of apsides CD, on which lies the fixed point A (the position of the Sun) at a known 'eccentric' distance AB (all previously determined from Tycho's observations), where B is the midpoint of CD. (From now on, as a convenience, we shall use the algebraic notation BC = BD = , AB = , even though it is an anachronism.)
Figure 1Kepler started from the initial framework illustrated in Figure (1), which could be described as standard Ptolemaic, except that Kepler automatically transposed it from geocentric to heliocentric mode. He adopted the traditional mechanism of deferent, epicycle, and eccentric, being aware, as the Ancients had been, that motion in the circle of radius centred on A, when combined with motion in the epicyclet of radius ZQ = AB = (whose centre Z lies on the deferent), together produce a motion of Q equivalent to a simple motion of Q round the eccentric circle centre B radius . (Mathematicians may like to regard ABQZ as a 'parallelogram of circular motions'.) We shall specify the typical point of any of the three successive orbits proposed by Kepler just as he did - determined by the angle at the centre of the eccentric circle, which we shall denote by β for distinctiveness. (This usage was authenticated by tradition, since in ancient astronomy motions consisted of combinations of rotations which were measured by the angles at the centres of their respective circles.) Then we have corresponding angles from the parallels AZ and BQ, so that:
∠QBC = ∠ZAB = β.
This angle β is called 'the eccentric anomaly' in both ancient and modern astronomy (though we shall avoid that name here). The ordinate QH is also extremely significant in Kepler's reasoning, as we shall demonstrate, concentrating on the three main stages of Kepler's progress once he had adopted the approach which would provide a rational route to his goal.
At the first stage Kepler took Q on the eccentric circle as the typical point and so he tested the eccentric itself as a proposed path. However, he found that this placed the planet too far from the Sun in almost all positions. So he finally rejected the idea that each planet moved in a single circle, and set out to find the actual curve that was the planet's path - naturally, this had to be constructed from a combination of (arcs of) circles by the geometry of Euclid, since Kepler recognized nothing else as appropriate for the heavens.
Figure 2The typical points of the three successive proposed paths are all named, and the separate constructions shown, in Figure (2). It is evident that the structure needed to produce these points already, or potentially, exists in Figure (1) in terms of a chosen value QBC = β. This is significant because - as we will see in Section 7 - the time is also expressed in terms of β, so a common value of β ensures simultaneity. The three-stage procedure that Kepler adopted was to take geometrically-defined points (K', K'', K) along AZ, one at each stage in turn, then with centre A to draw the corresponding circular arc (radius AK', AK'', AK), so that each arc would end at a geometrically-defined point (Q, V, P) respectively. The stages are classified according to the chapters of Astronomia Nova Ⓣ in whch each construction appears:
- First stage (Chs.39-44): large-grade curve - outer bound. In this special case, AQ = AK' is constructed, but the typical point is already known to be Q, on the eccentric.
- Second stage (Chs.45-50): small-grade curve - inner bound. K'' lies on the eccentric, and AV = AK'' is constructed, to specify typical point V lying on the epicycle. (Kepler tried many variations at this stage, but this is the only ovoid to be properly defined).
- Third stage: medial-grade curve (Chs.51-60) - observationally satisfactory. K lies where the perpendicular from Q meets AZ, and AP = AK is constructed, to specify typical point P lying on the ordinate QH.
Figure 3So the resulting radius vector AP that finally satisfied Kepler (in Ch.58) was quantified geometrically from the constructed rectangle AKQR, by applying nothing more than a Euclidean - straightedge-and-compasses - construction, as shown in Figure (3):
AP = AK = QR = BQ + BR.
This relationship is nowadays known as Law I.
[It is expressed in modern terms for reference in the Summary Table at the end: also see the article Planetary motion tackled kinematically.]
However, such a construction had never been invented before and Kepler did not have the slightest idea what curve the above relationship represented. However, he did know that if the curve were an ellipse, the typical point P would satisfy a vital condition that he had come across in the work of Archimedes: On Conoids and Spheroids Prop.4 (where it was stated as if well known even then):
PH/QH = BF/BC
There is good reason to believe that this was the earliest plane definition of an ellipse, (because it can be derived directly from a section of a cone in three easy steps [1]), as well as the definition most commonly, if not exclusively, used by Kepler's contemporaries: it is just the ratio-property of the ordinates. Some people nowadays will recognize it as the 'compressed circle' property.
The identification of the curve as an ellipse also depends on a relationship that Kepler established in Ch. 59, Prop. VII, which we express here in modern terms (writing BF = to denote the minor semiaxis), recognizing that will now represent the (focal) eccentricity:
. (1)
This may appropriately be called the 'focus-fixing property' of an ellipse, since it determines the position of the focus when the major and minor semiaxes are known. Kepler had already invented the term 'focus' in Astronomiae Pars Optica Ⓣ (1604) in connection with his work on vision, though he did not realize its connection with his astronomy at that juncture - in Astronomia Nova Ⓣ he simply referred to the point A as punctum eccentricum, or eccentric point. Nevertheless, the position of the focus of this particular ellipse is crucial. Unless its focus coincides with the fixed Sun (the origin), the investigation would have been too complicated to manage by geometry. Actually, Kepler's approach was successful just because the ellipse is simpler than any circle in this situation - an unlikely assertion which is proved in Planetary motion tackled kinematically.
In Astronomia Nova Ⓣ Ch. 59, Prop. XI, Kepler set out a rigorous geometrical proof that the typical point he had constructed satisfied the ratio-property which defines an ellipse. Hence, there can be no suggestion that Kepler merely selected an ellipse and checked it against observations (as many readers may have been told). Because of its importance the proof has been reproduced more than once [2]; though modernized in style, and reordered - to increase its impact - clearly it has not been altered in substance, since it relies on nothing more 'advanced' than Pythagoras' Theorem, and properties of similar triangles. Thus (apart from the use of definition (1) above) the proof is entirely based on cited or implied propositions from Euclid's Elements. Incidentally, this provides additional confirmation of my contention (in Section 5) that Kepler did not rely on the Conics of Apollonius for his discovery of the ellipse - in his astronomy he simply did not need anything so sophisticated.
Kepler set out a rigorous geometrical proof that the typical point he had constructed satisfied the ratio-property which defines an ellipse. Hence, there can be no suggestion that Kepler merely selected an ellipse and checked it against observations (as many readers may have been told). Because of its importance the proof has been reproduced several times [2]; though modernized in style, and reordered - to increase its impact - clearly it has not been altered in substance, since it relies on nothing more 'advanced' than Pythagoras' Theorem, and properties of similar triangles. Thus (apart from the use of relationship (1) above) the proof is entirely based on cited or implied propositions from Euclid's Elements. Incidentally, this provides additional confirmation of my contention (in Section 5) that Kepler did not rely on the Conics of Apollonius for his discovery of the ellipse - in his astronomy he simply did not need anything so sophisticated.
7. Constructing the representation of time
This investigation took place alongside, but independently of, the construction of the path of the planet. From a heliocentric point of view, it is especially easy to be aware that planets move more slowly the further they are from the Sun (and faster when nearer). Thus, as Kepler realized, a connection exists between a small (micro) interval of time and the corresponding distance of the planet from the Sun. Kepler's practical problem in Astronomia Nova Ⓣ, however, was to discover a way of measuring the time taken to reach the typical position (P) of the planet at an intermediate point of the orbit. Initially, he suggested that this (macro) time (the sum of the micro intervals of time) could be represented geometrically by the sum of all the corresponding distances from the Sun. In Ch.40, at the first of the three stages set out in Section 6, Kepler put this into practice, by citing Archimedes, Measurement of a Circle, Prop.3, to justify him in taking a sum of distances to be equivalent to the area of a sector of a circle.
Figure 4Next, Kepler extended that proposition, and took the distance-sum from the eccentric point (A, the position of the Sun) to be (approximately) proportional to the area of the eccentric sector (the area QAC, shown in Figure (4)). Then he demonstrated geometrically how to find the area of such a sector (devising alternative ways of splitting up the area as he required them):
Eccentric sector QAC = circle sector QBC + ΔQBA = segment QHC + ΔQHA.
At the second stage, various doubts and distractions arose, but these were put aside by the third stage, when Kepler discovered that the path was an ellipse (as described in Section 6). In Ch.59, Prop.III, he applied the ratio-property of the ordinates, illustrated in Figure (5), to obtain:
(Segment PHC) / (Segment QHC) = .
Similarly, by Elements I, 39 we have:
ΔPHA / ΔQHA = .
Figure 5Using these two results, again from Figure (5), Kepler deduced:
Ellipse sector PAC = ellipse segment PHC + ΔPHA = (segment QHC + ΔQHA).
Hence,
Ellipse sector PAC = circle sector QAC.
So, at the end of Astronomia Nova Ⓣ, Kepler had discovered that, when the planet's path was an ellipse, time in orbit appeared to be precisely proportional to the area swept out. Thus the area representation was altogether satisfactory in providing an inherently quantifiable measure of time. (Kepler regarded his initial suggestion, the distance-sum representation, as rather unsatisfactory because it did not give a geometrical interpretation, and so could not provide an exact result. Fortunately, the apparent irreconcilability of the two representations motivated him eventually to come to a more precise understanding of the mathematics of an elliptic orbit: see [3].)
[In modern algebraic terms it is easy to establish, from Figure (5), that:
Area of circle sector QAC =
and,
Area of ellipse sector PAC = .
Since both areas are proportional to the time, from either relation one can deduce that:
Time .
The result is derived otherwise in Planetary motion tackled kinematically.]
The above relationship, expressing Time ∝ Area in its most precise formulation, is nowadays known as Law II. It appears for reference in the Summary Table at the end.
8. Kepler's subsequent justification of the two laws
This is where the accounts of Kepler's work generally stop - but Kepler achieved much more. Firstly, between 1609 and 1618, he satisfied himself that the orbit of each of the six primary planets was an ellipse with the Sun at one focus. He went on to tackle the problem of the motions of planets, and their causes, in Epitome Astronomiae Copernicanae Ⓣ. This consists of seven books, though only Book V (1621), supported in places by Book IV (1620), contains the really innovative work. Despite the title, it epitomizes Keplerian, rather than Copernican astronomy. And further confirmation of the motions is given in Harmonice Mundi Ⓣ, 1618 Book V, Chapter 3, where there are some quantified references to a single planet, in addition to the main discussion which involves the planetary system. Unfortunately, Kepler's investigation of the motions was little appreciated by his contemporaries, and largely ignored subsequently. However, the overall success of his theory was confirmed in practice through the Rudolphine Tables (1627) - which, unlike other astronomical tables, remained observationally accurate and useful for many decades: see Kepler. These tables were calculated in terms of β, which can now be identified as the auxiliary angle of the ellipse. The mathematical treatment carried out in Planetary motion tackled kinematically demonstrates that this angle is the uniquely appropriate foundation for a structure which is simple because it depends on orthogonality and therefore is the only workable basis for Kepler's astronomy.
9. Essential orthogonality of the components of motion and their associated causes
Figure 6In De Caelo Ⓣ I, 3, Aristotle had declared that there were only two simple motions, circular and linear. Accordingly, on this authority, Kepler was able to match each one of the pair of results (the curve, and the independently-determined representation of time) that he had discovered in Astronomia Nova Ⓣ, to one of these mutually perpendicular components of motion. So this introduces another instance of the Principle of Orthogonal Independence (in fact dated earlier than Euclid). These components are listed in the Summary Table at the end for reference, and illustrated in Figure (6) by solid arrows:
- radial motion which is measured by the linear variation in distance from the Sun;
- transradial motion which is measured by the variation in the area swept out: this motion is defined to be circular round the Sun, and thus precisely at right angles to the radial motion. (It is called 'transverse motion' by some mathematicians.) Indeed, had Kepler realized that one of the motions attributed to the planet is strictly (though instantaneously) circular, he would surely have been pleased that the Platonic precept (see Section 3) had not been entirely abandoned after all.
Neither was Kepler's approach to the problem of causes of motion in any mathematical sense an anticipation of the work of Newton (despite the views of some previous commentators); it was, by contrast, governed by his background in the Aristotelian tradition. Though this Aristotelian 'physics' was becoming outdated even in Kepler's day, people still believed that an object would not move unless there was a 'force' or cause of motion to make it do so. Also, this 'force' had to act by contact; and, the object would then move only in the direction of the 'force', while the amount of 'force' was responsible for the amount of motion produced. Kepler could never have supposed that the Sun could exert an attractive force because that concept did not exist in Aristotelian terms.
10. The Sun's rotation: the cause of transradial motion
We will deal first with the cause of the transradial motion because the revolution of the planets round the Sun is the most outstanding feature of a heliocentric universe, and requires a universal cause. Kepler accounted for that motion by inventing the rotation of the Sun on its axis. He suggested this a few years before the rotation was actually established, c.1610, from observations of sunspots by Galileo, Scheiner (a minor contemporary astronomer), and independently by Harriot (c.1560-1621). Thus, Kepler envisaged that the rays emitted by the rotating Sun would 'hit' or impel each planet continuously round in a circle. Naturally, he expected that this impulsion would be less when the planet was further from the Sun, so he reasonably supposed that the action of the rays would vary inverse-linearly (that is, weaken) with distance. Amazingly, the formulation of this cause then exactly agrees with the evaluation of the transradial motion set out in the Summary Table at the end, as is confirmed by the modern treatment in Planetary motion tackled kinematically.
11. Magnetism: the cause of radial motion
To account for radial motion, Kepler obviously needed a cause that would be individual to each planet, because every planetary ellipse is a different shape. He selected magnetism, having come across a recently-published book, De Magnete Ⓣ, 1600 by Gilbert (1544-1603), which stated that the Earth should be regarded as a giant magnet. Because of his Copernican convictions, Kepler extended this idea to suppose that every planet possessed magnetism, and contained a set of 'fibres' fixed within its body which could be activated by the Sun's magnetism; and he further supposed that each set of fibres possessed a unique potential magnetic 'strength' that could be associated with the individual eccentricity of the particular planetary path. Unfortunately the way this cause was supposed to function cannot be associated with action at a distance (because this was a nonAristotelian concept). Thus it is not correct - nor is it meaningful - to interpret Kepler's magnetism as a 'force', either in an Aristotelean or in a modern context. The radial motion itself was evaluated by taking a small variation (an increment) of the distance from the Sun with respect to a small change in the auxiliary angle: see Summary Table at the end, confirmed by the modern treatment in Planetary motion tackled kinematically. Ultimately the cause provided its own justification - because the radial motion it produced is sound in mathematical terms.
12. The associated pair of orthogonal causes
Kepler was the first to introduce the concept of causation into astronomy, and in accordance with his Copernican convictions, he naturally believed that the Sun was the generator of all causes. Moreover, it seemed common sense to suppose that the Sun could only act (or activate) continuously either in a radial direction or circularly round itself, and this consideration, for Kepler, determined the direction of the causes available and limited their number to two. Thus the causes (as well as the motions and the constituents of the orbit) were also subject to the operation of the Principle of Orthogonal Independence.
Hence, each of the pair of perpendicular component motions illustrated in Figure (6) can be matched to its own distinct cause, as indicated in the Summary Table at the end, in accordance with the Principle of Economy (another relic of Aristotle) - one cause per motion. We summarize Kepler's final suppositions:
- The precedent cause was the action of the Sun's rays, due to its rotation, which produced transradial motion. This constituted an entirely acceptable Aristotelian 'force', satisfying the three conditions listed in Section 9;
- The lesser cause was magnetism, generated by the Sun, which activated the planetary fibres. The Sun appeared to function merely as a catalyst to facilitate radial motion - on no account can it be regarded as a Newtonian force (nor as an Aristotelian 'force').
13. Conclusion: the criterion of simplicity
Kepler was able to formulate a complete account of planetary motion using only elementary geometry, and accordingly we will highlight the two overriding reasons for his achievement, putting them in a historical context. They are both new to Keplerian analysis.
- Kinematics (not dynamics): the one-body problem
It was not until 1687 that Newton (1642-1727) gave a quantified definition of mass [4]. (That watershed book also contained a sophisticated treatment of tangential velocity in orbit, as well as formulating a concept of acceleration to accompany the concept of attractive force.) Thus it is clear that Kepler could not have been aware of the modern implication of (the dimension of) mass in the solar system, though his interpretation of an orbit certainly involved the dimensions both of length and of time, as we have demonstrated. Hence we can now recognize that Kepler's work was entirely kinematical, and acknowledge that he was, then, absolutely justified in treating each individual planet as if it were the only particle in the universe apart from the fixed Sun. This is the process that was described (in Section 4) as idealization because it ensured an exact solution (of the one-body problem) which was uniquely simple. It is interesting that an analogous situation occurred in the work of Galileo, Kepler's contemporary, when he idealized the motion of a projectile (as a perfect parabola) by neglecting air resistance. The solutions reached in each case are in some senses provisional, but they are certainly vital steps on the way to the presentday solution.
- Orthogonality
There is a further analogy with the work of Galileo, who also introduced orthogonal components of motion for the study of projectiles. However, unlike Kepler, these components were horizontal and vertical, but like Kepler, Galileo never felt the need to investigate the existence of a single 'resultant' motion, nor to attempt to determine its direction. (In all other respects, the methods of the two were quite different.) The table below shows the fundamentally orthogonal structure of Kepler's planetary astronomy. Remarkably, this account forms a coherent package into which a further cause could not have been fitted. (This explains the absence of mention of 'gravity' anywhere in this analysis - it is tentatively introduced only in some separate discussions of the Earth-Moon system: it would have been altogether redundant in Kepler's work on planetary orbits.)
| Summary of Kepler's orthogonal astronomy (for a single planet) | ||
|---|---|---|
| Associated with Law II Transradial direction | Features | Associated with Law I Radial direction |
| Area | Constituents of orbit | Ellipse path |
| Coordinates (in terms of β) | ||
| δ or δ | Components of motion | |
| Action circularly round Sun: perpendicular to Sun's rays | Direction of components | Activation in direction of Sun, though fibres are supposed fixed in direction |
| 'Impulsion' of Sun's rays | Keplerian causes | [Strength of planet's fibres |
References (show)
- A E L Davis, 'Some plane geometry from a cone: the focal distance of an ellipse at a glance', Mathematical Gazette, forthcoming July 2007.
- A E L Davis, 'Kepler's Road to Damascus', Centaurus 35 (1992) pp.156-157;
- A E L Davis, Kepler's unintentional ellipse - a celestial detective story, Mathematical Gazette 82, no.493 (1998), p.42;
- A E L Davis: 'The Mathematics of the Area Law: Kepler's successful proof in Epitome Astronomiae Copernicanae (1621)', Archive for History of Exact Sciences 57, 5 (2003), especially Section 6.
- Isaac Newton: The Mathematical Principles of Natural Philosophy, London 1687.
Written by A E L Davis, University College, London.
Last Update October 2006
Last Update October 2006