Johannes Kepler
Quick Info
Weil der Stadt, Württemberg, Holy Roman Empire (now Germany)
Regensburg (now in Germany)
Biography
Johannes Kepler is now chiefly remembered for discovering the three laws of planetary motion that bear his name published in 1609 and 1619). He also did important work in optics (1604, 1611), discovered two new regular polyhedra (1619), gave the first mathematical treatment of close packing of equal spheres (leading to an explanation of the shape of the cells of a honeycomb, 1611), gave the first proof of how logarithms worked (1624), and devised a method of finding the volumes of solids of revolution that (with hindsight!) can be seen as contributing to the development of calculus (1615, 1616). Moreover, he calculated the most exact astronomical tables hitherto known, whose continued accuracy did much to establish the truth of heliocentric astronomy (Rudolphine Tables, Ulm, 1627).A large quantity of Kepler's correspondence survives. Many of his letters are almost the equivalent of a scientific paper (there were as yet no scientific journals), and correspondents seem to have kept them because they were interesting. In consequence, we know rather a lot about Kepler's life, and indeed about his character. It is partly because of this that Kepler has had something of a career as a more or less fictional character (see historiographic note below).
Childhood
Kepler was born in the small town of Weil der Stadt in Swabia and moved to nearby Leonberg with his parents in 1576. His father was a mercenary soldier and his mother the daughter of an innkeeper. Johannes was their first child. His father left home for the last time when Johannes was five, and is believed to have died in the war in the Netherlands. As a child, Kepler lived with his mother in his grandfather's inn. He tells us that he used to help by serving in the inn. One imagines customers were sometimes bemused by the child's unusual competence at arithmetic.
Kepler's early education was in a local school and then at a nearby seminary, from which, intending to be ordained, he went on to enrol at the University of Tübingen, then (as now) a bastion of Lutheran orthodoxy.
Kepler's opinions
Throughout his life, Kepler was a profoundly religious man. All his writings contain numerous references to God, and he saw his work as a fulfilment of his Christian duty to understand the works of God. Man being, as Kepler believed, made in the image of God, was clearly capable of understanding the Universe that He had created. Moreover, Kepler was convinced that God had made the Universe according to a mathematical plan (a belief found in the works of Plato and associated with Pythagoras). Since it was generally accepted at the time that mathematics provided a secure method of arriving at truths about the world (Euclid's common notions and postulates being regarded as actually true), we have here a strategy for understanding the Universe. Since some authors have given Kepler a name for irrationality, it is worth noting that this rather hopeful epistemology is very far indeed from the mystic's conviction that things can only be understood in an imprecise way that relies upon insights that are not subject to reason. Kepler does indeed repeatedly thank God for granting him insights, but the insights are presented as rational.
University education
At this time, it was usual for all students at a university to attend courses on "mathematics". In principle this included the four mathematical sciences: arithmetic, geometry, astronomy and music. It seems, however, that what was taught depended on the particular university. At Tübingen Kepler was taught astronomy by one of the leading astronomers of the day, Michael Mästlin (1550 - 1631). The astronomy of the curriculum was, of course, geocentric astronomy, that is the current version of the Ptolemaic system, in which all seven planets - Moon, Mercury, Venus, Sun, Mars, Jupiter and Saturn - moved round the Earth, their positions against the fixed stars being calculated by combining circular motions. This system was more or less in accord with current (Aristotelian) notions of physics, though there were certain difficulties, such as whether one might consider as 'uniform' (and therefore acceptable as obviously eternal) a circular motion that was not uniform about its own centre but about another point (called an 'equant'). However, it seems that on the whole astronomers (who saw themselves as 'mathematicians') were content to carry on calculating positions of planets and leave it to natural philosophers to worry about whether the mathematical models corresponded to physical mechanisms. Kepler did not take this attitude. His earliest published work (1596) proposes to consider the actual paths of the planets, not the circles used to construct them.
At Tübingen, Kepler studied not only mathematics but also Greek and Hebrew (both necessary for reading the scriptures in their original languages). Teaching was in Latin. At the end of his first year Kepler got 'A's for everything except mathematics. Probably Mästlin was trying to tell him he could do better, because Kepler was in fact one of the select pupils to whom he chose to teach more advanced astronomy by introducing them to the new, heliocentric cosmological system of Copernicus. It was from Mästlin that Kepler learned that the preface to On the revolutions, explaining that this was 'only mathematics', was not by Copernicus. Kepler seems to have accepted almost instantly that the Copernican system was physically true; his reasons for accepting it will be discussed in connection with his first cosmological model (see below).
It seems that even in Kepler's student days there were indications that his religious beliefs were not entirely in accord with the orthodox Lutheranism current in Tübingen and formulated in the Confessio Augustana Ⓣ. Kepler's problems with this Protestant orthodoxy concerned the supposed relation between matter and 'spirit' (a non-material entity) in the doctrine of the Eucharist. This ties up with Kepler's astronomy to the extent that he apparently found somewhat similar intellectual difficulties in explaining how 'force' [See the History Topic on Kepler's planetary laws] from the Sun could affect the planets. In his writings, Kepler is given to laying his opinions on the line - which is very convenient for historians. In real life, it seems likely that a similar tendency to openness led the authorities at Tübingen to entertain well-founded doubts about his religious orthodoxy. These may explain why Mästlin persuaded Kepler to abandon plans for ordination and instead take up a post teaching mathematics in Graz. Religious intolerance sharpened in the following years. Kepler was excommunicated in 1612. This caused him much pain, but despite his (by then) relatively high social standing, as Imperial Mathematician, he never succeeded in getting the ban lifted.
Kepler's first cosmological model (1596)
Instead of the seven planets in standard geocentric astronomy the Copernican system had only six, the Moon having become a body of kind previously unknown to astronomy, which Kepler was later to call a 'satellite' (a name he coined in 1610 to describe the moons that Galileo had discovered were orbiting Jupiter, literally meaning 'attendant'). Why six planets?
Moreover, in geocentric astronomy there was no way of using observations to find the relative sizes of the planetary orbs; they were simply assumed to be in contact. This seemed to require no explanation, since it fitted nicely with natural philosophers' belief that the whole system was turned from the movement of the outermost sphere, one (or maybe two) beyond the sphere of the 'fixed' stars (the ones whose pattern made the constellations), beyond the sphere of Saturn. In the Copernican system, the fact that the annual component of each planetary motion was a reflection of the annual motion of the Earth allowed one to use observations to calculate the size of each planet's path, and it turned out that there were huge spaces between the planets. Why these particular spaces?
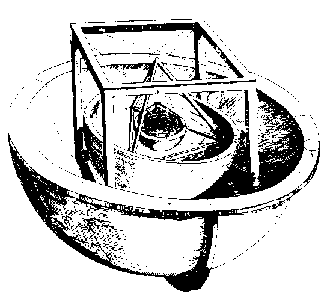
Kepler's answer to these questions, described in his Mysterium cosmographicum Ⓣ, Tübingen, 1596, looks bizarre to twentieth-century readers (see the figure on the right). He suggested that if a sphere were drawn to touch the inside of the path of Saturn, and a cube were inscribed in the sphere, then the sphere inscribed in that cube would be the sphere circumscribing the path of Jupiter. Then if a regular tetrahedron were drawn in the sphere inscribing the path of Jupiter, the insphere of the tetrahedron would be the sphere circumscribing the path of Mars, and so inwards, putting the regular dodecahedron between Mars and Earth, the regular icosahedron between Earth and Venus, and the regular octahedron between Venus and Mercury. This explains the number of planets perfectly: there are only five convex regular solids (as is proved in Euclid's Elements , Book 13). It also gives a convincing fit with the sizes of the paths as deduced by Copernicus, the greatest error being less than 10% (which is spectacularly good for a cosmological model even now). Kepler did not express himself in terms of percentage errors, and his is in fact the first mathematical cosmological model, but it is easy to see why he believed that the observational evidence supported his theory.
Kepler saw his cosmological theory as providing evidence for the Copernican theory. Before presenting his own theory he gave arguments to establish the plausibility of the Copernican theory itself. Kepler asserts that its advantages over the geocentric theory are in its greater explanatory power. For instance, the Copernican theory can explain why Venus and Mercury are never seen very far from the Sun (they lie between Earth and the Sun) whereas in the geocentric theory there is no explanation of this fact. Kepler lists nine such questions in the first chapter of the Mysterium cosmographicum Ⓣ.
Kepler carried out this work while he was teaching in Graz, but the book was seen through the press in Tübingen by Mästlin. The agreement with values deduced from observation was not exact, and Kepler hoped that better observations would improve the agreement, so he sent a copy of the Mysterium cosmographicum to one of the foremost observational astronomers of the time, Tycho Brahe (1546 - 1601). Tycho, then working in Prague (at that time the capital of the Holy Roman Empire), had in fact already written to Mästlin in search of a mathematical assistant. Kepler got the job.
The 'War with Mars'
Naturally enough, Tycho's priorities were not the same as Kepler's, and Kepler soon found himself working on the intractable problem of the orbit of Mars [See the History Topic on Kepler's planetary laws]. He continued to work on this after Tycho died (in 1601) and Kepler succeeded him as Imperial Mathematician. Conventionally, orbits were compounded of circles, and rather few observational values were required to fix the relative radii and positions of the circles. Tycho had made a huge number of observations and Kepler determined to make the best possible use of them. Essentially, he had so many observations available that once he had constructed a possible orbit he was able to check it against further observations until satisfactory agreement was reached. Kepler concluded that the orbit of Mars was an ellipse with the Sun in one of its foci (a result which when extended to all the planets is now called "Kepler's First Law"), and that a line joining the planet to the Sun swept out equal areas in equal times as the planet described its orbit ("Kepler's Second Law"), that is the area is used as a measure of time. After this work was published in Astronomia nova, ... Ⓣ, Heidelberg, 1609, Kepler found orbits for the other planets, thus establishing that the two laws held for them too. Both laws relate the motion of the planet to the Sun; Kepler's Copernicanism was crucial to his reasoning and to his deductions.
The actual process of calculation for Mars was immensely laborious - there are nearly a thousand surviving folio sheets of arithmetic - and Kepler himself refers to this work as 'my war with Mars', but the result was an orbit which agrees with modern results so exactly that the comparison has to make allowance for secular changes in the orbit since Kepler's time.
Observational error
It was crucial to Kepler's method of checking possible orbits against observations that he have an idea of what should be accepted as adequate agreement. From this arises the first explicit use of the concept of observational error. Kepler may have owed this notion at least partly to Tycho, who made detailed checks on the performance of his instruments (see the biography of Brahe).
Optics, and the New Star of 1604
The work on Mars was essentially completed by 1605, but there were delays in getting the book published. Meanwhile, in response to concerns about the different apparent diameter of the Moon when observed directly and when observed using a camera obscura, Kepler did some work on optics, and came up with the first correct mathematical theory of the camera obscura and the first correct explanation of the working of the human eye, with an upside-down picture formed on the retina. These results were published in Ad Vitellionem paralipomena, quibus astronomiae pars optica traditur Ⓣ, Frankfurt, 1604. He also wrote about the New Star of 1604, now usually called 'Kepler's supernova', rejecting numerous explanations, and remarking at one point that of course this star could just be a special creation 'but before we come to [that] I think we should try everything else' De stella nova Ⓣ, Prague, 1606, Chapter 22, KGW 1, p. 257, line 23.
Following Galileo's use of the telescope in discovering the moons of Jupiter, published in his Sidereal Messenger (Venice, 1610), to which Kepler had written an enthusiastic reply (1610), Kepler wrote a study of the properties of lenses (the first such work on optics) in which he presented a new design of telescope, using two convex lenses (Dioptrice, Prague, 1611). This design, in which the final image is inverted, was so successful that it is now usually known not as a Keplerian telescope but simply as the astronomical telescope.
Leaving Prague for Linz
Kepler's years in Prague were relatively peaceful, and scientifically extremely productive. In fact, even when things went badly, he seems never to have allowed external circumstances to prevent him from getting on with his work. Things began to go very badly in late 1611. First, his seven year old son died. Kepler wrote to a friend that this death was particularly hard to bear because the child reminded him so much of himself at that age. Then Kepler's wife died. Then the Emperor Rudolf, whose health was failing, was forced to abdicate in favour of his brother Matthias, who, like Rudolf, was a Catholic but (unlike Rudolf) did not believe in tolerance of Protestants. Kepler had to leave Prague. Before he departed he had his wife's body moved into the son's grave, and wrote a Latin epitaph for them. He and his remaining children moved to Linz (now in Austria).
Marriage and wine barrels
Kepler seems to have married his first wife, Barbara, for love (though the marriage was arranged through a broker). The second marriage, in 1613, was a matter of practical necessity; he needed someone to look after the children. Kepler's new wife, Susanna, had a crash course in Kepler's character: the dedicatory letter to the resultant book explains that at the wedding celebrations he noticed that the volumes of wine barrels were estimated by means of a rod slipped in diagonally through the bung-hole, and he began to wonder how that could work. The result was a study of the volumes of solids of revolution Nova stereometria doliorum ... Ⓣ, Linz, 1615, in which Kepler, basing himself on the work of Archimedes, used a resolution into 'indivisibles'. This method was later developed by Bonaventura Cavalieri (c. 1598 - 1647) and is part of the ancestry of the infinitesimal calculus.
The Harmony of the World
Kepler's main task as Imperial Mathematician was to write astronomical tables, based on Tycho's observations, but what he really wanted to do was write The Harmony of the World, planned since 1599 as a development of his Mystery of the Cosmos. This second work on cosmology (Harmonices mundi libri V Ⓣ, Linz, 1619) presents a more elaborate mathematical model than the earlier one, though the polyhedra are still there. The mathematics in this work includes the first systematic treatment of tessellations, a proof that there are only thirteen convex uniform polyhedra (the Archimedean solids) and the first account of two non-convex regular polyhedra (all in Book 2). The Harmony of the World also contains what is now known as 'Kepler's Third Law', that for any two planets the ratio of the squares of their periods will be the same as the ratio of the cubes of the mean radii of their orbits. From the first, Kepler had sought a rule relating the sizes of the orbits to the periods, but there was no slow series of steps towards this law as there had been towards the other two. In fact, although the Third Law plays an important part in some of the final sections of the printed version of the Harmony of the World, it was not actually discovered until the work was in press. Kepler made last-minute revisions. He himself tells the story of the eventual success:-
...and if you want the exact moment in time, it was conceived mentally on 8th March in this year one thousand six hundred and eighteen, but submitted to calculation in an unlucky way, and therefore rejected as false, and finally returning on the 15th of May and adopting a new line of attack, stormed the darkness of my mind. So strong was the support from the combination of my labour of seventeen years on the observations of Brahe and the present study, which conspired together, that at first I believed I was dreaming, and assuming my conclusion among my basic premises. But it is absolutely certain and exact that "the proportion between the periodic times of any two planets is precisely the sesquialterate proportion of their mean distances ..."Witchcraft trial
(Harmonice mundi Book 5, Chapter 3, trans. Aiton, Duncan and Field, p. 411).
While Kepler was working on his Harmony of the World, his mother was charged with witchcraft. He enlisted the help of the legal faculty at Tübingen. Katharina Kepler was eventually released, at least partly as a result of technical objections arising from the authorities' failure to follow the correct legal procedures in the use of torture. The surviving documents are chilling. However, Kepler continued to work. In the coach, on his journey to Württemberg to defend his mother, he read a work on music theory by Vincenzo Galilei (c.1520 - 1591, Galileo's father), to which there are numerous references in The Harmony of the World.
Astronomical Tables
Calculating tables, the normal business for an astronomer, always involved heavy arithmetic. Kepler was accordingly delighted when in 1616 he came across Napier's work on logarithms (published in 1614). However, Mästlin promptly told him first that it was unseemly for a serious mathematician to rejoice over a mere aid to calculation and second that it was unwise to trust logarithms because no-one understood how they worked. (Similar comments were made about computers in the early 1960s.) Kepler's answer to the second objection was to publish a proof of how logarithms worked, based on an impeccably respectable source: Euclid's Elements Book 5. Kepler calculated tables of eight-figure logarithms, which were published with the Rudolphine Tables (Ulm, 1628). The astronomical tables used not only Tycho's observations, but also Kepler's first two laws. All astronomical tables that made use of new observations were accurate for the first few years after publication. What was remarkable about the Rudolphine Tables was that they proved to be accurate over decades. And as the years mounted up, the continued accuracy of the tables was, naturally, seen as an argument for the correctness of Kepler's laws, and thus for the correctness of the heliocentric astronomy. Kepler's fulfilment of his dull official task as Imperial Mathematician led to the fulfilment of his dearest wish, to help establish Copernicanism.
Wallenstein
By the time the Rudolphine Tables were published Kepler was, in fact, no longer working for the Emperor (he had left Linz in 1626), but for Albrecht von Wallenstein (1583 - 1632), one of the few successful military leaders in the Thirty Years' War (1618 - 1648).
Wallenstein, like the emperor Rudolf, expected Kepler to give him advice based on astrology. Kepler naturally had to obey, but repeatedly points out that he does not believe precise predictions can be made. Like most people of the time, Kepler accepted the principle of astrology, that heavenly bodies could influence what happened on Earth (the clearest examples being the Sun causing the seasons and the Moon the tides) but as a Copernican he did not believe in the physical reality of the constellations. His astrology was based only on the angles between the positions of heavenly bodies ('astrological aspects'). He expresses utter contempt for the complicated systems of conventional astrology.
Death
Kepler died in Regensburg, after a short illness. He was staying in the city on his way to collect some money owing to him in connection with the Rudolphine Tables. He was buried in the local church, but this was destroyed in the course of the Thirty Years' War and nothing remains of the tomb.
Historiographic note
Much has sometimes been made of supposedly non-rational elements in Kepler's scientific activity. Believing astrologers frequently claim his work provides a scientifically respectable antecedent to their own. In his influential Sleepwalkers the late Arthur Koestler made Kepler's battle with Mars into an argument for the inherent irrationality of modern science. There have been many tacit followers of these two persuasions. Both are, however, based on very partial reading of Kepler's work. In particular, Koestler seems not to have had the mathematical expertise to understand Kepler's procedures. Closer study shows Koestler was simply mistaken in his assessment.
The truly important non-rational element in Kepler's work is his Christianity. Kepler's extensive and successful use of mathematics makes his work look 'modern', but we are in fact dealing with a Christian Natural Philosopher, for whom understanding the nature of the Universe included understanding the nature of its Creator.
References (show)
- O Gingerich, Biography in Dictionary of Scientific Biography (New York 1970-1990).
See THIS LINK. - Biography in Encyclopaedia Britannica.
http://www.britannica.com/biography/Johannes-Kepler - A Armitage, John Kepler (1966).
- C Baumgardt, Johannes Kepler : Life and Letters (New York, N. Y., 1951).
- M Caspar, Kepler (Germany, 1948).
- M Dickreiter, Der Musiktheoretiker Johannes Kepler (Berne and Munich, 1973).
- J L E Dreyer, A History of Astronomy from Thales to Kepler (New York, 1953).
- J V Field, Kepler's Geometrical Cosmology (Chicago, 1988).
- W Gerlach, Johannes Kepler zum 400. Geburtstag (Munich, 1972).
- W Gerlach and M List, Johannes Kepler : Leben und Werk (Munich, 1966, 1980).
- W Gerlach and M List, Johannes Kepler (1571 Weil der Stadt - 1630 Regensburg) (Munich, 1971).
- E Goldbeck, Keplers Lehre von der Gravitation, Reprint of the 1896 original (Hildesheim, 1980).
- J Hemleben, Johannes Kepler in Selbstzeugnissen und Bilddokumenten (Reinbek, 1971).
- J Hoppe, Johannes Kepler : Biographien Hervorragender Naturwissenschaftler, Techniker und Mediziner (Leipzig, 1987).
- J Kepler (translated A M Duncan, commentary E J Aiton), Mysterium cosmographicum. The secret of the Universe (New York, 1981).
- J Kepler (translated W Donahue), Astronomia nova: New Astronomy Cambridge, 1992)
- J Kepler (translated E J Aiton, A M Duncan, J V Field), The Harmony of the World, Memoirs of the American Philosophical Society, 209, (Philadelphia, 1997).
- A Koestler, The Watershed: A Biography of Johannes Kepler (1984).
- E Oeser, Kepler (German) (Göttingen-Zurich, 1971).
- G Simon, Kepler - astronome, astrologue (Paris, 1979).
- B Stephenson, Kepler's physical astronomy. Reprint of the 1987 original (Princeton, NJ, 1994).
- A Van Helden, Measuring the Universe: Cosmic dimensions from Aristarchus to Halley (Chicago and London, 1985).
- K Walter, Johannes Kepler und Tübigen (Tubingen, 1971).
- H Wussing, Kepler, in H Wussing and W Arnold, Biographien bedeutender Mathematiker (Berlin, 1983).
- E J Aiton, Kepler's path to the construction and rejection of his first oval orbit for Mars, Ann. of Sci. 35 (2) (1978), 173-190.
- E J Aiton, Johannes Kepler in the light of recent research, Hist. of Sci. 14 (2) (1976), 77-100.
- E J Aiton, How Kepler discovered the elliptical orbit, Math. Gaz. 59 (410) (1975), 250-260.
- E J Aiton, Kepler and the 'Mysterium Cosmographicum', Sudhoffs Arch. 61 (2) (1977), 173-194.
- W Applebaum, Donne's meeting with Kepler: a previously unknown episode, Philological Quarterly 50 (1) (1971), 132 - 4
- E Badolati, On the history of Kepler's equation, Vistas Astronom. 28 (1-2) (1985), 343-345.
- B S Baigrie, The justification of Kepler's ellipse, Stud. Hist. Philos. Sci. 21 (4) (1990), 633-664.
- B S Baigrie, Kepler's laws of planetary motion, before and after Newton's 'Principia' : an essay on the transformation of scientific problems, Stud. Hist. Philos. Sci. 18 (2) (1987), 177-208.
- P Barker and B R Goldstein, Distance and velocity in Kepler's astronomy, Ann. of Sci. 51 (4) (1994), 59-73.
- A Beer and P Beer (editors), Johannes Kepler. Four hundred years: Proceedings of conferences held in honour of Johannes Kepler, Vistas in Astronomy 18 (1975)
- A Beer and J V Field, Kepler - his times, his work, his life and 400 years, Scientia (Milano) 114 (9-12) (1979), 585-599.
- Ju A Belyi, Johannes Kepler (on the 400th anniversary of his birth) (Russian), Voprosy Istor. Estestvoznan. i Tehn. Vyp. 3-4 (36-37) (1971), 107-116, 206.
- Ju A Belyj, and D Trifunovi'c, Zur Geschichte der Logarithmentafeln Keplers, NTM Schr. Geschichte Naturwiss. Tech. Medizin 9 (1) (1972), 5-20.
- V Bialas, Keplers komplizierter Weg zur Wahrheit : von neuen Schwierigkeiten, die 'Astronomia Nova' zu lesen, Ber. Wiss.-Gesch. 13 (3) (1990), 167-176.
- V Bialas and E Papadimitriou, Materialien zu den Ephemeriden von Johannes Kepler, Bayer. Akad. Wiss. Math.-Natur. Kl. Abh. (N.F.) 159 (1980).
- W Blaschke, Galilei und Kepler, Hamburger Math. Einzelschr. 39 (1943).
- J Blum and W Helmchen, Von Kepler zu Newton. Von den Planetenbahnen zum Gravitationsgesetz, Praxis Math. 29 (4) (1987), 193-199.
- S Bochner, Kepler : a personal footnote, Vistas Astronom. 22 (1) (1978), 19-20.
- J B Brackenridge, Kepler, elliptical orbits, and celestial circularity : a study in the persistence of metaphysical commitment. II, Ann. of Sci. 39 (3) (1982), 265-295.
- J B Brackenridge, Kepler, elliptical orbits, and celestial circularity : a study in the persistence of metaphysical commitment. I, Ann. of Sci. 39 (2) (1982), 117-143.
- G Buchdahl, Methodological aspects of Kepler's theory of refraction. Johannes Kepler : b. 1571, d. 1630, Studies in Hist. and Philos. Sci. 3 (1972), 265-298.
- C de Buzon, Remarques sur l'interprétation de l'oeuvre de Kepler, Arch. Internat. Histoire Sci. 27 (100) (1977), 72-81.
- G Cifoletti, Kepler's 'De quantitatibus', Ann. of Sci. 43 (3) (1986), 213-238.
- A C Crombie, Expectation, modelling and assent in the history of optics. II, Kepler and Descartes, Stud. Hist. Philos. Sci. 22 (1) (1991), 89-115.
- Yu A Danilov and Ya A Smorodinskii, Johannes Kepler : from the mystery to the harmony, Soviet Physics Uspekhi 16 (1973), 136-155.
- A E L Davis, Kepler's physical framework for planetary motion, Centaurus 35 (2) (1992), 165-191.
- A E L Davis, Kepler's road to Damascus, Centaurus 35 (2) (1992), 143-164.
- A E L Davis, Grading the eggs (Kepler's sizing-procedure for the planetary orbit), Centaurus 35 (2) (1992), 121-142.
- A E L Davis, Kepler's 'distance law' - myth not reality, Centaurus 35 (2) (1992), 103-120.
- A E L Davis, Kepler's resolution of individual planetary motion, Centaurus 35 (2) (1992), 97-102.
- A E L Davis, Kepler, the ultimate Aristotelian, Acta historiae rerum naturalium necnon technicarum 2 (1998), 65 - 73.
- W H Donahue, Kepler's approach to the oval of 1602, from the Mars notebook, J. Hist. Astronom. 27 (4) (1996), 281-295.
- W H Donahue, Kepler's invention of the second planetary law, British J. Hist. Sci. 27 (92, 1) (1994), 89-102.
- W H Donahue, Kepler's first thoughts on oval orbits : text, translation, and commentary, J. Hist. Astronom. 24 (1-2) (1993), 71-100.
- W H Donahue, Kepler's fabricated figures : covering up the mess in the 'New astronomy', J. Hist. Astronom. 19 (4) (1988), 217-237.
- S Drake, Galileo, Kepler, and the phases of Venus, Journal for the history of astronomy 15 (1984), 198-208.
- S Drake, Galileo's 'Platonic' cosmogony and Kepler's 'Prodromus', J. Hist. Astronom. 4 (3) (1973), 174-191.
- A M Duncan, Kepler on light and sound, Acta historiae rerum naturalium necnon technicarum 2 (1998), 98 - 103.
- A Elena, On the different kinds of attractive forces in Kepler, Arch. Internat. Hist. Sci. 33 (110) (1983), 22-29.
- J Evans, The division of the Martian eccentricity from Hipparchos to Kepler : a history of the approximations to Kepler motion, Amer. J. Phys. 56 (11) (1988), 1009-1024.
- J V Field, Kepler's rejection of solid celestial spheres, Vistas Astronom. 23 (3) (1979), 207-211.
- J V Field, Kepler's star polyhedra, Vistas Astronom. 23 (2) (1979), 109-141.
- J V Field, Kepler's cosmological theories: their agreement with observation, Quarterly Journal of the Royal Astronomical Society 23 (1982), 556 - 68.
- J V Field, Kepler's Rejection of Numerology in B W Vickers (ed.), Occult and Scientific Mentalities in the Renaissance (Cambridge, 1984), 273-296.
- J V Field, A Lutheran Astrologer : Johannes Kepler, Archive for History of Exact Science 31 (1984), 189-.
- J V Field, Two mathematical inventions in Kepler's 'Ad Vitellionem paralipomena', Stud. Hist. Philos. Sci. 17 (4) (1986), 449-468.
- J V Field, What is scientific about a scientific instrument?, Nuncius III (2) (1988), 3 - 26.
- J V Field, The relation between geometry and algebra: Cardano and Kepler on the regular heptagon in E.Kessler (ed.), Girolamo Cardano: Philosoph, Naturforscher, Arzt (Wiesbaden, 1994), 219 - 242.
- J V Field, Rediscovering the Archimedean polyhedra: Piero della Francesca, Luca Pacioli, Leonardo da Vinci, Albrecht Dürer, Daniele Barbaro, and Johannes Kepler, Archive for History of Exact Sciences 50 (1997), 241 - 289.
- J V Field, Kepler's mathematization of cosmology, Acta historiae rerum naturalium necnon technicarum 2 (1998), 27 - 48.
- A Franklin and C Howson, Newton and Kepler, a Bayesian approach, Stud. Hist. Philos. Sci. 16 (4) (1985), 379-385.
- W Gerlach, Johannes Kepler und die Copernicanische Wende, Nova Acta Leopoldina (N.F.) 37 (210) (1972).
- W Gerlach, Humor und Witz in Schriften von Johannes Kepler, Bayer. Akad. Wiss. Math.-Natur. Kl. S.-B. (1968), 13-30.
- O Gingerich, Johannes Kepler, in Planetary astronomy from the Renaissance to the rise of astrophysics Part A (Cambridge, 1989), 54-78.
- D Gronau, Johannes Kepler und die Logarithmen, Berichte der Mathematisch-Statistischen Sektion in der Forschungsgesellschaft Joanneum 284 (Graz, 1987).
- R Haase, Keplers Weltharmonik in Vergangenheit, Gegenwart und Zukunft, Sudhoffs Arch. 57 (1973), 41-70.
- J Halbronn, Les historiens des sciences face à l'activité astrologique de Képler, in Proceedings of the 104th National Congress of Learned Societies (Paris, 1979), 135-145.
- F Hallyn, Kepler, Snell and the law of refraction (Dutch), Med. Konink. Acad. Wetensch. Belgie 56 (2) (1994), 119-134.
- F Hammer, Die Astrologie des Johannes Kepler, Sudhoffs Arch. 55 (1971), 113-135.
- J E Hofmann, Johannes Kepler als Mathematiker. II, Praxis Math. 13 (12) (1971), 318-324.
- J E Hofmann, Johannes Kepler als Mathematiker. I, Praxis Math. 13 (11) (1971), 287-293.
- J F Hofmann, Über Keplers Ellipsenrektifikation, RETE 1 (3-4) (1971/72), 301-310.
- S H Hollingdale, A note on Kepler's solar system, Bull. Inst. Math. Appl. 22 (3-4) (1986), 34-37.
- G Holton, Johannes Kepler's universe : its physics and metaphysics, Amer. J. Phys. 24 (1956), 340-351.
- G Hon, On Kepler's awareness of the problem of experimental error, Ann. of Sci. 44 (6) (1987), 545-591.
- U Hoyer, Kepler's celestial mechanics, Vistas Astronom. 23 (1) (1979), 69-74.
- K-N Ihmig, Trägheit und Massebegriff bei Johannes Kepler, Philos. Natur. 27 (2) (1990), 156-205.
- U Klein, Keplers Bemühungen um die Harmonieschriften des Ptolemaios und Porphyrios, Johannes Kepler Werk und Leistung (Linz, 1971), 51 - 60.
- S A Kleiner, A new look at Kepler and abductive argument, Stud. Hist. Philos. Sci. 14 (4) (1983), 279-313.
- A Koyré, La gravitation universelle de Kepler à Newton, Arch. Internat. Hist. Sci. (N.S.) 4 (1951), 638-653.
- F Krafft, Erfahrung und Vorurteil im naturwissenschaftlichen Denken Johannes Keplers, Ber. Wiss.-Gesch. 14 (2) (1991), 73-76.
- F Krafft, Astronomie als Gottesdienst. Die Erneuerung der Astronomie durch Johannes Kepler, in Der Weg der Naturwissenschaft von Johannes von Gmunden zu Johannes Kepler (Vienna, 1988), 182-196.
- F Krafft, Keplers Wissenschaftspraxis und -verständnis, Sudhoffs Arch. 59 (1) (1975), 54-68.
- V Maeyama, Kepler's hypothesis vicaria, Arch. Hist. Exact Sci. 41 (1) (1990), 53-92.
- A Malet, Gregorie, Descartes, Kepler, and the law of refraction, Arch. Internat. Hist. Sci. 40 (125) (1990), 278-304.
- A Malet, Keplerian illusions : geometrical pictures vs optical images in Kepler's visual theory, Stud. Hist. Philos. Sci. 21 (1) (1990), 1-40.
- J Marek, Kepler's inventions in physical optics, in 1971 Actes XIIe Congrès Internat. d'Histoire des Sciences III B : Science et Philosophie : XVIIe et XVIIIe Siècles (Paris, 1971), 81-87.
- A A Mikhailov, Kepler and modern science (Russian), Voprosy Istor. Estestvoznan. i Tekhn. (4) (1980), 133-135.
- C-U Moulines, Intertheoretic approximation : the Kepler-Newton case, Synthese 45 (3) (1980), 387-412.
- G Nádor, Kepler's world view and role in the development of the notion of law of nature (Hungarian), Magyar Tud. Akad. Mat. Fiz. Oszt. Közl. 4 (1954), 219-227.
- O Neugebauer, Notes on Kepler, Comm. Pure Appl. Math. 14 (1961), 593-597.
- A Postl, Correspondence between Kepler and Galileo, Vistas Astronom. 21 (4) (1977), 325-330.
- E Rosen, Galileo and Kepler: Their First Two Contacts, Isis 57 (1966), 262-264.
- I Schneider, Wahrscheinlichkeit und Zufall bei Kepler, Philos. Natur. 16 (1) (1976/77), 40-63.
- O B Sheynin, J Kepler as a statistician, Bull. Inst. Internat. Statist. 46 (2) (1975), 341-354, 355-360.
- B Stephenson, Kepler's physical astronomy, Studies in the History of Mathematics and Physical Sciences 13 (New York-Berlin, 1987).
- S Straker, Kepler, Tycho, and the 'optical part of astronomy' : the genesis of Kepler's theory of pinhole images, Arch. Hist. Exact Sci. 24 (4) (1981), 267-293.
- N M Swerdlow, Shadow measurement : the 'Sciametria' from Kepler's 'Hipparchus' - a translation with commentary, in The investigation of difficult things (Cambridge, 1992), 19-70.
- S Thorvaldsen, Did Kepler 'prove' the planetary laws? (Norwegian), Normat 33 (2) (1985), 76-87, 100.
- S Thorvaldsen, Kepler's path to the planetary laws (Norwegian), Normat 31 (2) (1983), 49-58.
- P Urban and N Pucker, Johannes Kepler : sa contribution au progrès des sciences naturelles, Ontologie und Logik/Ontology and logic (Berlin, 1979), 247-265.
- J Vuillemin, La méthodologie de Kepler, in Traditionen und Perspektiven der analytischen Philosophie (Vienna, 1989), 24-34.
- B Wandt, Die geplante Berufung von Johannes Kepler an die Universität Rostock (1629/30), NTM Schr. Geschichte Natur. Tech. Medizin 19 (1) (1982), 77-84.
- R S Westman, Kepler's theory of hypothesis and the 'realist dilemma'. Johannes Kepler : b. 1571, d. 1630, Studies in Hist. and Philos. Sci. 3 (1972), 233-264.
- R S Westman, The comet and the cosmos : Kepler, Mastlin and the Copernican hypothesis, in Études sur l'audience de la théorie héliocentrique (Wrocław, 1972), 7-30.
- D T Whiteside, Kepler, Newton and Flamsteed on refraction through a 'regular aire' : the mathematical and the practical, Centaurus 24 (1980), 288-315.
Additional Resources (show)
Other pages about Johannes Kepler:
Other websites about Johannes Kepler:
- Dictionary of Scientific Biography
- Encyclopaedia Britannica
- Johannes Kepler Working Group
- NNDB
- Plus Magazine (Kepler's proofs)
- The Galileo Project
- Science Museum Florence
- Kevin Brown (Kepler and the third law)
- AMS (The Kepler sphere packing problem)
- George W Hart (Kepler's polyhedra)
- Sci Hi blog
- Sci Hi blog (2)
- A Google doodle
- History of Computing Project
- A Giorgilli
- Linda Hall
- Linda Hall (2)
- Linda Hall (3)
- Linda Hall (4)
- Mathematical Genealogy Project
- MathSciNet Author profile
Honours (show)
Honours awarded to Johannes Kepler
Cross-references (show)
- History Topics: A brief history of cosmology
- History Topics: A history of the calculus
- History Topics: Christianity and the Mathematical Sciences - the Heliocentric Hypothesis
- History Topics: General relativity
- History Topics: Kepler's Planetary Laws
- History Topics: Light through the ages: Ancient Greece to Maxwell
- History Topics: Mathematics and the physical world
- History Topics: Orbits and gravitation
- History Topics: Science in the 17th century: From Europe to St Andrews
- History Topics: The Golden ratio
- History Topics: The Missing Planet
- History Topics: The Size of the Universe
- History Topics: The mathematician and the forger
- History Topics: Theories of gravitation
- History Topics: Thomas Harriot's manuscripts
- Famous Curves: Ellipse
- Famous Curves: Folium
- Societies: International Astronomical Union
- Other: 11th October
- Other: 1954 ICM - Amsterdam
- Other: 2009 Most popular biographies
- Other: 24th February
- Other: 7th August
- Other: 8th October
- Other: Earliest Known Uses of Some of the Words of Mathematics (C)
- Other: Earliest Known Uses of Some of the Words of Mathematics (D)
- Other: Earliest Known Uses of Some of the Words of Mathematics (F)
- Other: Earliest Known Uses of Some of the Words of Mathematics (S)
- Other: Earliest Known Uses of Some of the Words of Mathematics (T)
- Other: Earliest Uses of Function Symbols
- Other: Earliest Uses of Symbols for Fractions
- Other: Jeff Miller's postage stamps
- Other: Linda Hall Library links
- Other: Most popular biographies – 2024
- Other: Popular biographies 2018
- Other: Sci Hi blog links
- Other: The Dynamics of the Solar System
- Other: The Structure of the Solar System
Written by J. V. Field, London
Last Update April 1999
Last Update April 1999
