The Golden ratio
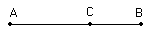
Euclid, in The Elements, says that the line is divided in extreme and mean ratio by if .
Although Euclid does not use the term, we shall call this the golden ratio. The definition appears in Book VI but there is a construction given in Book II, Theorem 11, concerning areas which is solved by dividing a line in the golden ratio. As well as constructions to divide a line in the golden ratio, Euclid gives applications such as the construction of a regular pentagon, an icosahedron and a dodecahedron. Here is how the golden ratio comes into the construction of a pentagon.
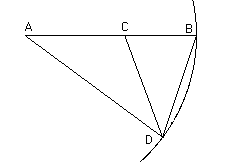
First construct an isosceles triangle whose base angles are double the vertex angle. This is done by taking a line and marking on the line in the golden ratio. Then draw a circle with centre radius . Mark on the circle so that . The triangle has the property that its base angles are double its vertex angle.
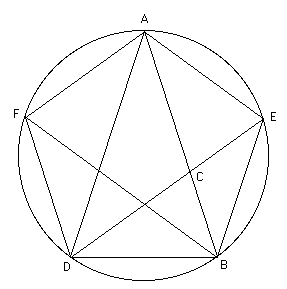
Now starting with such a triangle draw a circle through and . Then bisect the angle with the line meeting the circle at . Note that the line passes through , the point dividing in the golden ratio. Similarly construct and draw the pentagon .
Of course nobody believes that Euclid's Elements represents original work so there is the question of who studied the golden ratio before Euclid. Now some historians believe that Book II of The Elements covers material originally studied by Theodorus of Cyrene while others attribute the material to Pythagoras, or at least to the Pythagoreans. Proclus, writing in the fifth century AD, claims:-
Eudoxus ... multiplied the number of propositions concerning the section which had their origin in Plato, employing the method of analysis for their solution.
Many believe that by 'section' Proclus means 'golden ratio'. Eudoxus certainly attended lectures by Plato so it is entirely reasonable that he might work on topics suggested during these lectures. Heath writes in his edition of Euclid's Elements:-
This idea that Plato began the study of [the golden ratio] as a subject in itself is not in the least inconsistent with the supposition that the problem of Euclid II, 11 was solved by the Pythagoreans.Heath claims later in the same work that the construction of a pentagon using the isosceles triangle method referred to above was known to the Pythagoreans so there is a fair amount of evidence to suggest that this is where the study of the golden ratio began.
Hypsicles, around 150 BC, wrote on regular polyhedra. He is the author of what has been called Book XIV of Euclid's Elements, a work which deals with inscribing regular solids in a sphere. The golden ratio enters into the constructions.
Up to this time the golden ratio seems to have been considered as a geometrical property and there is no obvious sign that any attempt was made to associate a number with the ratio. Of course if has length 1 and where divides in the golden ratio, then we can use simple algebra to find .
gives so = .
Then the golden ratio is = = 1.6180339887498948482...
Heron certainly begins to compute approximate ratios, and in his work he gives approximate values for the ratio of the area of the pentagon to the area of the square of one side. With Ptolemy trigonometric tables, at least in terms of chords of circles, begin to be computed. He calculates the side of a regular pentagon in terms of the radius of the circumscribed circle.
Then the golden ratio is = = 1.6180339887498948482...
With the development of algebra by the Arabs one might expect to find the quadratic equation (or a related one) to that which we have given above. Al-Khwarizmi does indeed give several problems on dividing a line of length 10 into two parts and one of these does find a quadratic equation for the length of the smaller part of the line of length 10 divided in the golden ratio. There is no mention of the golden ratio, however, and it is unclear whether al-Khwarizmi is thinking of this particular problem.
Abu Kamil gives similar equations which arise from dividing a line of length 10 in various ways. Two of these ways are related to the golden ratio but again it is unclear whether Abu Kamil is aware of this. However, when Fibonacci produced Liber Abaci Ⓣ he used many Arabic sources and one of them was the problems of Abu Kamil. Fibonacci clearly indicates that he is aware of the connection between Abu Kamil's two problems and the golden ratio. In Liber Abaci Ⓣ he gives the lengths of the segments of a line of length 10 divided in the golden ratio as √125 -5 and 15 - √125.
Pacioli wrote Divina proportione Ⓣ which is his name for the golden ratio. The book contains little new on the topic, collecting results from Euclid and other sources on the golden ratio. He states (without any attempt at a proof or a reference) that the golden ratio cannot be rational. He also states the result given in Liber Abaci Ⓣ on the lengths of the segments of a line of length 10 divided in the golden ratio. There is little new in Pacioli's book which merely restates (usually without proof) results which had been published by other authors. Of course the title is interesting and Pacioli writes:
... it seems to me that the proper title for this treatise must be Divine Proportion. This is because there are very many similar attributes which I find in our proportion - all befitting God himself - which is the subject of our very useful discourse.He gives five such attributes, perhaps the most interesting being:-
... just like God cannot be properly defined, nor can be understood through words, likewise this proportion of ours cannot ever be designated through intelligible numbers, nor can it be expressed through any rational quantity, but always remains occult and secret, and is called irrational by the mathematicians.Cardan, Bombelli and others included problems in their texts on finding the golden ratio using quadratic equations. A surprising piece of information is contained in a copy of the 1509 edition of Pacioli's Euclid's Elements. Someone has written a note which clearly shows that they knew that the ratio of adjacent terms in the Fibonacci sequence tend to the golden number. Handwriting experts date the note as early 16th century so there is the intriguing question as to who wrote it. See [6] for further details.
The first known calculation of the golden ratio as a decimal was given in a letter written in 1597 by Michael Mästlin, at the University of Tübingen, to his former student Kepler. He gives "about 0.6180340" for the length of the longer segment of a line of length 1 divided in the golden ratio. The correct value is 0.61803398874989484821... . The mystical feeling for the golden ratio was of course attractive to Kepler, as was its relation to the regular solids. His writings on the topic are a mixture of good mathematics and magic. He, like the annotator of Pacioli's Euclid, knows that the ratio of adjacent terms of the Fibonacci sequence tends to the golden ratio and he states this explicitly in a letter he wrote in 1609.
The result that the quotients of adjacent terms of the Fibonacci sequence tend to the golden ratio is usually attributed to Simson who gave the result in 1753. We have just seen that he was not the first give the result and indeed Albert Girard also discovered it independently of Kepler. It appears in a publication of 1634 which appeared two years after Albert Girard's death.
In this article we have used the term golden ratio but this term was never used by any of the mathematicians whom we have noted above contributed to its development. We commented that "section" was possibly used by Proclus although some historians dispute that his reference to section means the golden ratio. The common term used by early writers was simply "division in extreme and mean ratio". Pacioli certainly introduced the term "divine proportion" and some later writers such as Ramus and Clavius adopted this term. Clavius also used the term "proportionally divided" and similar expressions appear in the works of other mathematicians. The term "continuous proportion" was also used.
The names now used are golden ratio, golden number or golden section. These terms are modern in the sense that they were introduced later than any of the work which we have discussed above. The first known use of the term appears in a footnote in Die reine Elementar-Matematik Ⓣ by Martin Ohm (the brother of Georg Simon Ohm):-
One is also in the habit of calling this division of an arbitrary line in two such parts the golden section; one sometimes also says in this case: the line r is divided in continuous proportion.The first edition of Martin Ohm's book appeared in 1826. The footnote just quoted does not appear and the text uses the term "continuous proportion". Clearly sometime between 1826 and 1835 the term "golden section" began to be used but its origin is a puzzle. It is fairly clear from Ohm's footnote that the term "golden section" is not due to him. Fowler, in [9], examines the evidence and reaches the conclusion that 1835 marks the first appearance of the term.
The golden ratio has been famed throughout history for its aesthetic properties and it is claimed that the architecture of Ancient Greece was strongly influenced by its use. The article [11] discusses whether the golden section is a universal natural phenomenon, to what extent it has been used by architects and painters, and whether there is a relationship with aesthetics.
References (show)
- R Herz-Fischler, A mathematical history of division in extreme and mean ratio (Waterloo, Ontario, 1987).
- R Herz-Fischler, A mathematical history of the golden number ( New York, 1998).
- E Ackermann, The golden section, Amer. Math. Monthly 2 (1895), 260-264.
- R Archibald, The golden section - Fibonacci series, Amer. Math. Monthly 25 (1918), 232-237.
- F Campan, The golden section (Romanian), Revista Stiintifica "V. Adamachi" 33 (1947). 225-231.
- L Curchin and R Herz-Fischler, De quand date le premier rapprochement entre la suite de Fibonacci et la division en extrême et moyenne raison?, Centaurus 28 (2) (1985), 129-138.
- R Fischler, On applications of the golden ratio in the visual arts, Leonardo 14 (1981), 31-32; 262-264; 349-351.
- R Fischler, How to find the golden number without really trying, Fibonacci Quart. 19 (1981), 406-410.
- D H Fowler, A generalization of the golden section, Fibonacci Quart. 20 (2) (1982), 146-158.
- J Kappraff, The relationship between mathematics and mysticism of the golden mean through history, in Fivefold symmetry (River Edge, NJ, 1992), 33-65.
- J Mawhin, Au carrefour des mathématiques, de la nature, de l'art et de l'ésotérisme: le nombre d'or, Rev. Questions Sci. 169 (2-3) (1998), 145-178.
- G Sarton, When did the term golden section or its equivalent in other languages originate, Isis 42 (1951), 47.
- A P Stakhov, The golden section in the measurement theory, in Symmetry 2: unifying human understanding, Part 2, Comput. Math. Appl. 17 (4-6) (1989), 613-638.
- A J van Zanten, The golden ratio in the arts of painting, building and mathematics, Nieuw Arch. Wisk. (4) 17 (2) (1999), 229-245.
Additional Resources (show)
Other websites about Golden ratio:
Written by J J O'Connor and E F Robertson
Last Update July 2001
Last Update July 2001