MacTutor
Earliest Uses of Function Symbols
The function symbol f(x) was first used by Leonhard Euler (1707-1783) in 1734 in Commentarii Academiae Scientiarum Petropolitanae (Cajori, vol. 2, page 268).
Absolute value function. Karl Weierstrass (1815-1897) used | | in an 1841 essay "Zur Theorie der Potenzreihen," in which the symbol appears on page 67. He also used the symbol in 1859 in "Neuer Beweis des Fundamentalsatzes der Algebra," in which the symbol appears on page 252. This latter essay was submitted to the Berlin Academy of Sciences on December 12, 1859. These are the two reference shown by Cajori (vol. 2, page 123).
Cajori says that the first essay was not printed at the time, and Julio González Cabillón believes neither paper was published until 1894, "when the welcome Erster Band [vol. I] of Karl Weierstrass "Mathematische Werke" [Berlin: Mayer & Mueller], saw the light. I do not know to what extent the editors could have interfered with Weierstrass manuscripts. In both papers the notation under discussion does not appear with a definition or with a further comment; thus I am speculating that their subsequent published typesetting might differ from that of Weierstrass original."
The memoir "Zur Theorie der eindeutigen analytischen Functionen," which appeared in Abhandlungen der Koeniglich Akademie der Wissenschaften [pp. 11-60, Berlin 1876, and was reprinted in Zweiter Band (volume II) of Weierstrass "Mathematische Werke" (1895)] has a footnote on page 78 in which Weierstrass remarks:
Ich bezeichne den absoluten Betrag einer complexen Groesse x mit |x|. [I denote the absolute value of complex number x by |x|]In this memoir, Weierstrass applied the absolute value symbolism to complex numbers.
Beta function. The use of β (for the function created by Euler) was introduced by Jacques P. M. Binet (1786-1856) in 1839 (Cajori, vol. 2, page 272).
Julio González Cabillón says the capital letter B is a common one in the Greek and Latin alphabets. If, after Legendre, the second Eulerian integral was known as the Gamma function, why Binet could not choose the initial of his name to denote the first Eulerian integral (Beta function), conventionally written as B(p,q). The citation: "Memoire sur les intégrales définies euleriennes, et sur leur application a la theorie des suites, ansi qu'a l'evaluation des fonctions des grands nombres," Journal de L'Ecole Royale Polytéchnique, Tome XVI, pp. 123-343, Paris, 1839.
On page 131 of his "Memoire...", Binet states:
Je designerai la premiere de ces fonctions par B(p,q), et pour la seconde j'adoptarai la notacion Gamma(p) proposee par M. Legendre.See also BETA and GAMMA FUNCTIONS on the math words page.
Gamma function. The use of Γ (for the function created by Euler) was introduced by Adrien-Marie Legendre (1752-1833) (Cajori vol. 2, page 271). On page 277 of his "Exercices de Calcul integral sur divers ordres de transcendantes et sur les quadrantes," Tome Premier, Paris, 1811, Legendre states:
... Cette quantité étant simplement fonction de a, nous la designerons par Γ(a), et nous ferons Γ(a) = .It is unknown why Legendre chose that letter, but Julio González Cabillón says compare capital letter L (Le Gendre) and the upside-down L. Or the relation between G (in Gendre) and G in Gamma. And there is also a nice relation between the gamma function and the contant C (= 0.577...). Letter C (the one that Euler actually used in his De progressionibus harmonicis observationes) is third in our alphabet; γ is also third in the Greek alphabet. Please mind that Legendre also used capital C to represent the famous Euler-Mascheroni constant (= 0.577...): On page 295 (ibidem) Legendre says:
C étant une constant dont la valeur calculée avec précision par une autre voie est C = 0,5772156649015325 donc enfin on aura, k étant très-petit ."See also BETA and GAMMA FUNCTIONS on the math words page.
Riemann's zeta function. The use of ζ for this function was introduced by Bernhard Riemann (1826-1866) as early as 1857 (Cajori vol. 2, page 278). It appears in "über die Anzahl der Primzahlen unter einer gegebenen Grösse" (1859) Werke (p. 138) English translation (p. 4). See RIEMANN HYPOTHESIS and RIEMANN ZETA FUNCTION on the Words page.
Bessel functions. P. A. Hansen used the letter J for this function in 1843 in Ermittelung der absoluten Störungen, although the designation of the index and argument has varied since then. Bessel himself used the letter I (Cajori vol. 2, page 279).
Logarithm function. Log. appears as an abbreviation for logarithm in A Description of the Admirable Table of Logarithmes (1616), an English translation by Edward Wright of Napier's work.
Log. (with a period, capital "L") was used by Johannes Kepler (1571-1630) in 1624 in Chilias logarithmorum (Cajori vol. 2, page 105)
log. (with a period, lower case "l") was used by Bonaventura Cavalieri (1598-1647) in Directorium generale Vranometricum in 1632 (Cajori vol. 2, page 106).
log (without a period, lower case "l") appears in the 1647 edition of Clavis mathematicae by William Oughtred (1574-1660) (Cajori vol. 1, page 193).
Kline (page 378) says Leibniz introduced the notation (showing no period), but he does not give a source.
was introduced by Edmund Gunter (1581-1626) according to an Internet source. [I do not see a reference for this in Cajori.]
In the Latin edition of his Introduction to Analysis of the Infinite (1748), Euler used l (the lower case letter) to denote a natural logarithm (which he called a hyperbolic logarithm). In the English translation by John D. Blanton, this has been replaced by log. [David Kullman]
ln (for natural logarithm) was used in 1893 by Irving Stringham (1847-1909) in Uniplanar Algebra (Cajori vol. 2, page 107).
William Oughtred (1574-1660) used a minus sign over the characteristic of a logarithm in the Clavis Mathematicae (Key to Mathematics), "except in the 1631 edition which does not consider logarithms" (Cajori vol. 2, page 110). The Clavis Mathematicae was composed around 1628 and published in 1631 (Smith 1958, page 393). Cajori shows a use from the 1652 edition.
Greatest integer function (floor function). Until recently [x] has been the standard symbol for the greatest integer function. According to Grinstein (1970), "The use of the bracket notation, which has led some authors to term this the bracket function, stems back to the work of Gauss (1808) in number theory. The function is also referred to by Legendre who used the now obsolete notation E(x)." The Gauss reference is to Theorematis arithmetici demonstratio nova. Werke Volume: Bd. 2 p. 5.
Recently the symbol
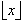has come into use. It was introduced in 1962 by Kenneth E. Iverson who also coined the name floor function. See CEILING FUNCTION and FLOOR FUNCTION on the Words page.
Use of arrows. Saunders Mc Lane, in Categories for the working mathematician (Springer-Verlag, 1971, p. 29), says: "The fundamental idea of representing a function by an arrow first appeared in topology about 1940, probably in papers or lectures by W. Hurewicz on relative homotopy groups. (W. Hurewicz: "On duality theorems," Bull. Am. Math. Soc. 47, 562-563) His initiative immediately attracted the attention of R. H. Fox and N. E. Steenrod, whose ... paper used arrows and (implicitly) functors... The arrow rapidly displaced the occasional notation (subset of ) for a function. It expressed well a central interest of topology. Thus a notation (the arrow) led to a concept (category)". [Arturo Mena]
José Ferreirós writes, "The function notation f(x) was Euler's, but it was only with Dedekind (mediated by ideas of Dirichlet and Riemann) that such notation was reconceived as a "mapping (function, Abbildung) of a set S" into another set (Ded 1888, no. 21). Dirichlet contributed the methodological shift which involves considering "arbitrary" functions. Riemann exploited the idea in the context of complex variables, and due to the peculiarities of the situation with analytic functions, he introduced the terminology of mappings (Abbildung): they are indeed conformal mappings! Dedekind moved this terminology into the most general case, and his mathematics revolve always around maps and morphisms. Dedekind had a very modern conception already, and introduces a whole set of very aptly chosen terms: image, identity map, composition of maps, injective maps ("similar" or "clear" mapping—the words work extremely well in the original German: deutliche oder klare Abbildung), mapping of a set into itself). The only thing that is missing is, precisely, the arrow notation. Now, the people who introduced it were, one way or another, under the influence of Dedekind. Ore was editor of his collected work, and his algebraic papers reflect a strong influence; similarly for Emmy Noether; and the same works for the Bourbaki people."
Sign, or signum, function. The symbol [a], to represent 0, 1, or -1, according to whether a is 0, positive, or negative, was introduced by Leopold Kronecker (1823-1891). He wrote:
Bezeichnet man naemlich mit [a] den Werth Null oder +1 oder -1, je nachdem die reelle Groesse a selbst gleich Null oder positiv oder negativ ist ... [February 14, 1878]This citation was provided by Julio González Cabillón