MacTutor
Earliest Uses of Symbols from Geometry
Lettering of geometric figures. The designation of points, lines, and planes by a letter or letters was in vogue among the ancient Greeks and has been traced back to Hippocrates of Chios (about 440 B. C.) (Cajori vol. 1, page 420, attributed to Moritz Cantor).
Lettering of triangles. Richard Rawlinson in a pamphlet prepared at Oxford sometime between 1655 and 1668 used A, B, C for the sides of a triangle and a, b, c for the opposite angles. In his notation, A was the largest side and C the smallest (Cajori vol. 2, page 162).
Leonhard Euler and Thomas Simpson reintroduced this scheme many years later, Euler using it in 1753 in Histoire de l'académie de Berlin (Cajori vol 2., page 162). Euler used capital letters for the angles.
In 1866, Karl Theodor Reye (1838-1919) proposed the plan of using capital letters for points, lower case letters for lines, and lower case Greek letters for planes in a remarkable two-volume work on geometry, Die Geometrie der Lage (Cajori vol. 1, page 423).
As early as 1618, an anonymous writer of the Appendix in the 1618 edition of Edward Wright's translation of John Napier's "Mirifici logarithmorum canonis descriptio" labeled the right angle of a triangle with the letter A:
It will bee conuenient in euery calculation, to haue in your view a triangle, described according to the present occasion: and if it bee a right angled triangle, to note it with Letters A.B.C: so that A may bee alwayes the right angle; B the angle at the Base B.A and C the angle at the Cathetus CA [sic].Cf. page 3 of "An Appendix to the Logarithmes of the Calculation of Triangles, and also a new and ready way for the exact finding out of such lines and logarithmes as are not precisely to be found in the Canons", in John Napier's "A description of the Admirable Table of Logarithmes ...", London, Printed for Simon Waterson, 1618
James W. L. Glaisher (1848-1928) has remarked that the letter A is taken to be the right angle in the right-angled triangle ABC in order that BA may represent the BAse, and CA the CAthetus, the first two initials indicating the words. The fact that this lettering was also employed by William Oughtred (1574-1660) in his books is one of the many arguments in support that Oughtred might be the author of the "Appendix" (Cajori vol. 2, p. 154).
Angle. Pierre Hérigone (1580-1643) used both
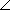and < in Cursus mathematicus. This work was published in 1634 and in a second edition in 1644. Cajori lists the symbols from the 1644 edition, which shows both angle symbols (Cajori vol. 1, page 202).
Arc. The arc symbol appears in the middle of the twelfth century in Plato of Tivoli's translation of the Liber embadorum by Savasorda (Cajori vol. 1, page 402).
Circle. Heron used a modified circle with a dot in the center to represent a circle around A. D. 150 (Cajori vol. 1, page 401).
Pappus used a circle with and without a dot in the center to represent a circle in the fourth century A. D. (Cajori vol. 1, page 401).
Triangle. Heron about A. D. 150 used a triangle as a symbol for triangle (Cajori).
Congruence. Gottfried Wilhelm Leibniz (1646-1716) introduced
for congruence in an unpublished manuscript of 1679 (Cajori vol. 1, page 414).
The first appearance in print of Leibniz's sign for congruence was in 1710 in the Miscellanea Berolinensia in the anonymous article "Monitum," which is attributed to Leibniz (Cajori vol. 2, page 195).
In 1777, Johann Friedrich Häseler (1732-1797) used
(with the tilde reversed) in Anfangsgründe der Arith., Alg., Geom. und Trig. (Lemgo), Elementar-Geometrie (Cajori vol. 1, page 415).
In 1824 Carl Brandan Mollweide (1774-1825) used the modern congruent symbol
in Euklid's Elemente (Cajori vol. 1, page 415).
Radius. Leonhard Euler introduced the use of R for the radius of the circumscribed circle and r for the radius of the inscribed circle (Boyer, page 495).
Degrees. The symbols for degrees, minutes, and seconds were used by Claudius Ptolemy (c. 85-c. 165) in the Almagest. However, the notation differed somewhat from the modern notation, and according to Cajori (vol. 2, page 143), "it is difficult to uphold" the view that our signs for degrees, minutes, and seconds are of Greek origin.
The first modern appearance of the degree symbol ° Cajori found is in the revised 1569 edition of Gemma Frisius, Arithmeticae practicae moethodus facilis by Gemma Frisius (1508-1555), although the symbol appears in the Appendix on astronomical fractions due to Jacques Peletier (1517-1582) and dated 1558. Cajori writes:
This is the first modern appearance that I have found of ° for integra or "degrees." It is explained that the denomination of the product of two such denominate numbers is obtained by combining the denominations of the factors; minutes times seconds give thirds, because 1+2=3. The denomination ° for integers or degrees is necessary to impart generality to this mode or procedure. "Integers when multiplied by seconds make seconds, when multiplied by thirds make thirds" (fol. 62, 76). It is possible that Peletier is the originator of the ° for degrees. But nowhere in this book have I been able to find the modern angular notation ° ' " used in writing angles. The ° is used only in multiplication.Erasmus Reinhold (1511-1553) used ° ' " in Prvtenicae tabulae coelestium motuum published in 1571 (Cajori).
Line segment. A bar above AB to indicate line segment AB was used in 1647 by Bonaventura Cavalieri (1598-1647) in Geometria indivisibilibae and Exercitationes geometriae sex, according to Cajori.
Slope. The earliest known use of m for slope appears in Vincenzo Riccati's memoir De methodo Hermanni ad locos geometricos resolvendos, which is chapter XII of the first part of his book Vincentii Riccati Opusculorum ad res Physica, & Mathematicas pertinentium (1757):
Propositio prima. Aequationes primi gradus construere. Ut Hermanni methodo utamor, danda est aequationi hujusmodi forma , quod semper fieri posse certum est. (p. 151)The reference is to the Swiss mathematician Jacob Hermann (1678-1733). This use of m was found by Dr. Sandro Caparrini of the Department of Mathematics at the University of Torino.
C. B. Boyer in his History of Analytic Geometry (1956, p. 205) points to a passage in Monge where the "modern point-slope form of plane equation of the straight line is given explicitly, perhaps for the first time." See "Mémoire sur la Théorie des Déblais et des Remblais," Histoire de l'Académie royale des sciences 1784 (Année 1781) p. 669.
In 1830, Traite Elementaire D'Arithmetique, A l'Usage De L'Ecole Centrale des Quatre-Nations: Par S.F. LaCroix, Dix-Huitieme Edition has [Karen Dee Michalowicz].
Another use of m occurs in 1842 in An Elementary Treatise on the Differential Calculus by Rev. Matthew O'Brien, from the bottom of page 1: "Thus in the general equation to a right line, namely , if we suppose the line..." [Dave Cohen].
O'Brien used m for slope again in 1844 in A Treatise on Plane Co-Ordinate Geometry [V. Frederick Rickey].
George Salmon (1819-1904), an Irish mathematician, used in his A Treatise on Conic Sections, which was published in several editions beginning in 1848. Salmon referred in several places to O'Brien's Conic Sections and it may be that he adopted O'Brien's notation. Salmon used a to denote the x-intercept, and gave the equation [David Wilkins].
Karen Dee Michalowicz has found an 1848 British analytic geometry text which has .
The 1855 edition of Isaac Todhunter's Treatise on Plane Co-Ordinate Geometry has [Dave Cohen].
In 1891, Differential and Integral Calculus by George A. Osborne has .
In Webster's New International Dictionary (1909), the "slope form" is .
In 1921, in An Introduction to Mathematical Analysis by Frank Loxley Griffin, the equation is written .
In Analytic Geometry (1924) by Arthur M. Harding and George W. Mullins, the "slope-intercept form" is .
In A Brief Course in Advanced Algebra by Buchanan and others (1937), the "slope form" is .
According to Erland Gadde, in Swedish textbooks the equation is usually written as . He writes that the technical Swedish word for "slope" is "riktningskoefficient", which literally means "direction coefficient," and he supposes k comes from "koefficient."
According to Dick Klingens, in the Netherlands the equation is usually written as or or . He writes that the Dutch word for slope is "richtingscoëfficiënt", which literally means "direction coefficient."
In Austria k is used for the slope, and d for the y-intercept.
According to Julio González Cabillón, in Uruguay the equation is usually written as or , and slope is called "pendiente," "coeficiente angular," or "parametro de direccion."
According to George Zeliger, "in Russian textbooks the equation was frequently written as , especially when plotting was involved. Since in Russian the slope is called 'the angle coefficient' and the word coefficient is spelled with k in the Cyrillic alphabet, usually nobody questioned the use of k. The use of b is less clear."
It is not known why the letter m was chosen for slope; the choice may have been arbitrary. John Conway has suggested m could stand for "modulus of slope." One high school algebra textbook says the reason for m is unknown, but remarks that it is interesting that the French word for "to climb" is monter. However, there is no evidence to make any such connection. Descartes, who was French, did not use m. In Mathematical Circles Revisited (1971) mathematics historian Howard W. Eves suggests "it just happened."
Parallelism. Two vertical bars, written horizontally and resembling the modern equal sign, were used by Heron about A. D. 150 and by Pappus (Cajori).
Thee parallel symbol written vertically was first used by William Oughtred (1574-1660) in Opuscula Mathematica Hactenus Inedita, which was published posthumously in 1677 (Cajori vol. 1, page 193).
John Kersey (1616-1677) also used the vertical parallel symbol. He used it after Oughtred, but in a work which was published before Oughtred. He used the symbol in Algebra, which was published in 1673. Kersey switched the lines from horizontal to vertical because of the adoption of the equal symbol (Cajori vol. 1, page 411).
Perpendicularity.
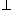was first used by Pierre Hérigone (1580-1643) in 1634 in Cursus mathematicus, which was published in five volumes from 1634 to 1637 (Cajori vol. 1, page 408). Johnson (page 149) says, "Herigone introduced so many new symbols in this six-volume work that some suggest that the introduction of these symbols, rather than an effective mathematics text, was his goal."
Right angle.
was used by Pappus (Cajori vol. 1, page 401).
Semi-perimeter. A capital S was first used by Leonhard Euler (1707-1783) in 1750 (Cajori 1919, page 235).
Similarity. ~ was introduced by Gottfried Wilhelm Leibniz (1646-1716) in a manuscripts of 1679 which were not published by him. The symbol was an S for similis, written sideways. The original manuscripts do not survive and it is uncertain whether the symbol Leibniz first used resembled the tilde or the tilde inverted (Cajori vol. 1, page 414).
In the manuscript of his Characteristica Geometrica he wrote: "similitudinem ita notabimus: a ~ b" (Cajori vol. 1, page 414).
The first appearance in print of Leibniz's sign for similarity was in 1710 in the Miscellanea Berolinensia in the anonymous article "Monitum," which is attributed to Leibniz (Cajori vol. 2, page 195).
S.S.S., S.W.S., and W.S.W. for the triangle congruence theorems and axioms were invented by Julius Worpitzky (1835-1895), professor at the Friedrich Werder Gymnasium in Berlin (Cajori vol. 1, page 424). (W for Winkel = angle)
An article in The Mathematics Teacher in March 1938 uses a.s.a. = a.s.a. and s.s.s. = s.s.s. and s.a.a. = s.a.a. as reasons in a proof. An article in the same journal in 1940 uses C.p.c.t.e., which is written out as "Corresponding parts of congruent triangles are equal."
An article in The Mathematics Teacher in April 1948 has: "The three common theorems on congruence of triangles (SAS = SAS; ASA = ASA; SSS = SSS) are 'proved' by superposition."