Indian Mathematics - Redressing the balance
Ian G Pearce
The Classical period: II. Aryabhata and his commentators
Aryabhata, who is occasionally known as Aryabhata I, or Aryabhata the elder to distinguish him from a tenth century astronomer of the same name, stands as a pioneer of the revival of Indian mathematics, and the so called 'classical period', or 'Golden era' of Indian mathematics. Arguably the Classical period continued until the 12th century, although in some respects it was over before Aryabhata's death following a costly, if ultimately successful, war with invading Huns which resulted in the eroding of the Gupta culture (D Duncan P 171). As mentioned, the classical period arose following a 'dark period' of significant political instability 200-400 AD, which caused the widespread stagnation of mathematical development.
We can accurately claim that Aryabhata was born in 476 AD, as he writes that he was 23 years old when he wrote his most significant mathematical work the Aryabhatiya (or Arya Bhateeya) in 499 AD. He was a member of the Kusuma Pura School, but is thought to have been a native of Kerala (in the extreme south of India), although unsurprisingly there is some debate. Further debate surrounds how important the work of Aryabhata actually was. In light of discoveries of both Vedic and Jaina mathematics it has been suggested that his work is of less significance mathematically. However as Gurjar claims it is more than likely that the majority, if not all prior mathematical work may not have been known to him, which makes his contribution remarkable. Either way, Aryabhata's work was to have massive influence on those who followed, in a similar way that the work of Luca Pacioli influenced the Italian renaissance mathematicians in the late 15th century.
As previously mentioned the only extant work of Aryabhata is his key work, the Aryabhatiya, a concise astronomical treatise of 118 verses written in a poetic form, of which 33 verses are concerned with mathematical rules. It is important here to point out that no proofs are contained with his rules, and this is perhaps a primary reason for the neglect by western scholars. As Indian mathematics is (generally) devoid of proof it is not considered 'true' mathematics in its purest sense. However I believe that adopting this stance is to deny the very origin of remarkable discoveries in mathematics, which may well have been the aim of Eurocentric scholars, as it allowed them to neglect the importance of Indian works in favour of European works.
In the mathematical verses of the Aryabhatiya the following topics are covered:
Arithmetic:
Method of inversion.
Various arithmetical operators, including the cube and cube root are though to have originated in Aryabhata's work. Aryabhata can also reliably be attributed with credit for using the relatively 'new' functions of squaring and square rooting.
Algebra:
Formulas for finding the sum of several types of series.
Rules for finding the number of terms of an arithmetical progression.
Rule of three - improvement on Bakshali Manuscript.
Rules for solving examples on interest - which led to the quadratic equation, it is clear that Aryabhata knew the solution of a quadratic equation.
Trigonometry:
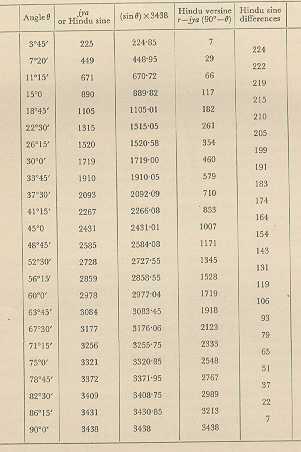
Tables of sines, not copied from Greek work (see Figure 8.2.1).
Gupta comments:
Geometry:
Area of a triangle, similar triangles, volume rules.
It has been suggested that Aryabhata's geometry was borrowed from the Jaina works, but this seems unlikely as it is generally accepted he would not have been familiar with them.
Also of relevance is the use of 'word numerals' and 'alphabet numerals', which are first found in Aryabhata's work. We can argue that this was not due to the absence of a satisfactory system of numeration but because it was helpful in poetry. C Srinivasiengar quaintly describes it as an:
With little doubt this is the most accurate approximation that had been given up to this point in the history of mathematics. Aryabhata found it from the circle with circumference 62832 and diameter 20000. Critics have tried to suggest that this approximation is of Greek origin. However with confidence it can be argued that the Greeks only used and and that no other values can be found in Greek texts.
I note with slight concern for the strength of my last comment that the Egyptian scholar Claudius Ptolemy derived the same value 300 years earlier, although there is no suggestion of a link between these two cases. Further to deriving this highly accurate value for , Aryabhata also appeared to be aware that it was an 'irrational' number and that his value was an approximation, which shows incredible insight. Thus even accepting that Ptolemy discovered the 4 decimal place value, there is no evidence that he was aware of the concept of irrationality, which is extremely important. Inexplicably Aryabhata preferred to use the approximation (= 3.1622) in practice!
Aryabhata's work on astronomy was also pioneering, and was far less tinged with a mythological flavour. Among many theories he was the first to suggest that diurnal motion of the 'heavens' is due to rotation of the earth about its axis, which is incredibly insightful (unsurprisingly he was criticised for this.)
In the field of 'pure' mathematics his most significant contribution was his solution to the indeterminate equation: ax - by = c
R Gupta states:
Example 8.2.1: Solution of 137x + 10 = 60y, as found in the Aryabhatiya.
Figure 8.2.1: Table of sines as found in the Aryabhatiya. [CS, P 48]
The work of Aryabhata was also extremely influential in India and many commentaries were written on his work (especially his Aryabhatiya). Among the most influential commentators were:
We can accurately claim that Aryabhata was born in 476 AD, as he writes that he was 23 years old when he wrote his most significant mathematical work the Aryabhatiya (or Arya Bhateeya) in 499 AD. He was a member of the Kusuma Pura School, but is thought to have been a native of Kerala (in the extreme south of India), although unsurprisingly there is some debate. Further debate surrounds how important the work of Aryabhata actually was. In light of discoveries of both Vedic and Jaina mathematics it has been suggested that his work is of less significance mathematically. However as Gurjar claims it is more than likely that the majority, if not all prior mathematical work may not have been known to him, which makes his contribution remarkable. Either way, Aryabhata's work was to have massive influence on those who followed, in a similar way that the work of Luca Pacioli influenced the Italian renaissance mathematicians in the late 15th century.
As previously mentioned the only extant work of Aryabhata is his key work, the Aryabhatiya, a concise astronomical treatise of 118 verses written in a poetic form, of which 33 verses are concerned with mathematical rules. It is important here to point out that no proofs are contained with his rules, and this is perhaps a primary reason for the neglect by western scholars. As Indian mathematics is (generally) devoid of proof it is not considered 'true' mathematics in its purest sense. However I believe that adopting this stance is to deny the very origin of remarkable discoveries in mathematics, which may well have been the aim of Eurocentric scholars, as it allowed them to neglect the importance of Indian works in favour of European works.
In the mathematical verses of the Aryabhatiya the following topics are covered:
Arithmetic:
Method of inversion.
Various arithmetical operators, including the cube and cube root are though to have originated in Aryabhata's work. Aryabhata can also reliably be attributed with credit for using the relatively 'new' functions of squaring and square rooting.
Algebra:
Formulas for finding the sum of several types of series.
Rules for finding the number of terms of an arithmetical progression.
Rule of three - improvement on Bakshali Manuscript.
Rules for solving examples on interest - which led to the quadratic equation, it is clear that Aryabhata knew the solution of a quadratic equation.
Trigonometry:
Tables of sines, not copied from Greek work (see Figure 8.2.1).
Gupta comments:
...The Aryabhatiya is the first historical work of the dated type, which definitely uses some of these (trigonometric) functions and contains a table of sines. [RG3, P 72]Spherical trigonometry (some incorrect).
Geometry:
Area of a triangle, similar triangles, volume rules.
It has been suggested that Aryabhata's geometry was borrowed from the Jaina works, but this seems unlikely as it is generally accepted he would not have been familiar with them.
Also of relevance is the use of 'word numerals' and 'alphabet numerals', which are first found in Aryabhata's work. We can argue that this was not due to the absence of a satisfactory system of numeration but because it was helpful in poetry. C Srinivasiengar quaintly describes it as an:
...Exceedingly queer, if original method of enumeration. [CS, P 43]However the work of Aryabhata also affords a proof that:
...The decimal system was well in vogue. [CS, P 43]Of the mathematics contained within the Aryabhatiya the most remarkable is an approximation for , which is surprisingly accurate. The value given is: = 3.1416
With little doubt this is the most accurate approximation that had been given up to this point in the history of mathematics. Aryabhata found it from the circle with circumference 62832 and diameter 20000. Critics have tried to suggest that this approximation is of Greek origin. However with confidence it can be argued that the Greeks only used and and that no other values can be found in Greek texts.
I note with slight concern for the strength of my last comment that the Egyptian scholar Claudius Ptolemy derived the same value 300 years earlier, although there is no suggestion of a link between these two cases. Further to deriving this highly accurate value for , Aryabhata also appeared to be aware that it was an 'irrational' number and that his value was an approximation, which shows incredible insight. Thus even accepting that Ptolemy discovered the 4 decimal place value, there is no evidence that he was aware of the concept of irrationality, which is extremely important. Inexplicably Aryabhata preferred to use the approximation (= 3.1622) in practice!
Aryabhata's work on astronomy was also pioneering, and was far less tinged with a mythological flavour. Among many theories he was the first to suggest that diurnal motion of the 'heavens' is due to rotation of the earth about its axis, which is incredibly insightful (unsurprisingly he was criticised for this.)
In the field of 'pure' mathematics his most significant contribution was his solution to the indeterminate equation: ax - by = c
R Gupta states:
...Aryabhata (also) made notable contributions to algebra [RG3, P73]Although Indian mathematics has become often ignored this was not always the case. The Aryabhatiya was translated into Arabic by Abu'l Hassan al-Ahwazi (before 1000 AD) as Zij al-Arjabhar and it is partly through this translation that Indian computational and mathematical methods were introduced to the Arabs, which will have had a significant effect on the forward progress made by mathematics. The historian A Cajori even goes as far as to suggest that:
...Diophantus, the father of Greek algebra, got the first algebraic knowledge from India. [RG4, P 12]This theory is supported by evidence that the eminent Greek mathematician Pythagoras visited India, which further 'throws open' the Eurocentric ideal.
Example 8.2.1: Solution of 137x + 10 = 60y, as found in the Aryabhatiya.
The general solution is found as follows:
137x + 10 = 60y
The following column of remainders, known as valli (vertical line) form is constructed:
2
3
1
1
The number of quotients, omitting the first one is 3. Hence we choose a multiplier such that on multiplication by the last residue, 1 (in red above), and subtracting 10 from the product the result is divisible by the penultimate remainder, 8 (in blue above). We have 1 × 18 - 10 = 1 × 8. We then form the following table:
This can be explained as such: The number 18, and the number above it in the first column, multiplied and added to the number below it, gives the last but one number in the second column. Thus, 18 × 1 + 1 = 19. The same process is applied to the second column, giving the third column, that is, 19 × 1 + 18 = 37. Similarly 37 × 3 + 19 = 130, 130 × 2 + 37 = 297.
Then x = 130, y = 297 are solutions of the given equation. Noting that 297 = 23 (mod 137) and 130 = 10 (mod 60), we get x = 10 and y = 23 as simple solutions. The general solution is x = 10 + 60m, y = 23 + 137m. If we stop with the remainder 8 in the process of division above then we can at once get x = 10 and y = 23. (Working omitted for sake of brevity).
This method was called Kuttaka, which literally means pulveriser, on account of the process of continued division that is carried out to obtain the solution.
137x + 10 = 60y
60) 137 (2 (60 divides into 137 twice with remainder 17, etc)
120
17( 60 ( 3
51
9) 17 ) 1
9
8 ) 9 (1
8
1
The following column of remainders, known as valli (vertical line) form is constructed:
2
3
1
1
The number of quotients, omitting the first one is 3. Hence we choose a multiplier such that on multiplication by the last residue, 1 (in red above), and subtracting 10 from the product the result is divisible by the penultimate remainder, 8 (in blue above). We have 1 × 18 - 10 = 1 × 8. We then form the following table:
2 2 2 2 297 3 3 3 130 130 1 1 37 37 1 19 19 The multiplier 18 18 Quotient obtained 1
This can be explained as such: The number 18, and the number above it in the first column, multiplied and added to the number below it, gives the last but one number in the second column. Thus, 18 × 1 + 1 = 19. The same process is applied to the second column, giving the third column, that is, 19 × 1 + 18 = 37. Similarly 37 × 3 + 19 = 130, 130 × 2 + 37 = 297.
Then x = 130, y = 297 are solutions of the given equation. Noting that 297 = 23 (mod 137) and 130 = 10 (mod 60), we get x = 10 and y = 23 as simple solutions. The general solution is x = 10 + 60m, y = 23 + 137m. If we stop with the remainder 8 in the process of division above then we can at once get x = 10 and y = 23. (Working omitted for sake of brevity).
This method was called Kuttaka, which literally means pulveriser, on account of the process of continued division that is carried out to obtain the solution.
Figure 8.2.1: Table of sines as found in the Aryabhatiya. [CS, P 48]

The work of Aryabhata was also extremely influential in India and many commentaries were written on his work (especially his Aryabhatiya). Among the most influential commentators were:
Bhaskara I (c 600-680 AD) also a prominent astronomer, his work in that area gave rise to an extremely accurate approximation for the sine function. His commentary of the Aryabhatiya is of only the mathematics sections, and he develops several of the ideas contained within. Perhaps his most important contribution was that which he made to the topic of algebra.
Lalla (c 720-790 AD) followed Aryabhata but in fact disagreed with much of his astronomical work. Of note was his use of Aryabhata's improved approximation of to the fourth decimal place. Lalla also composed a commentary on Brahmagupta's Khandakhadyaka.
Govindasvami (c 800-860 AD) his most important work was a commentary on Bhaskara I's astronomical work Mahabhaskariya, he also considered Aryabhata's sine tables and constructed a table which led to improved values.
Sankara Narayana (c 840-900 AD) wrote a commentary on Bhaskara I's work Laghubhaskariya (which in turn was based on the work of Aryabhata). Of note is his work on solving first order indeterminate equations, and also his use of the alternate 'katapayadi' numeration system (as well as Sanskrit place value numerals)
Following Aryabhata's death around 550 AD the work of Brahmagupta resulted in Indian mathematics attaining an even greater level of perfection. Between these two 'greats' of the classic period lived Yativrsabha, a little known Jain scholar, his work, primarily Tiloyapannatti, mainly concerned itself with various concepts of Jaina cosmology, and is worthy of minor note as it contained interesting considerations of infinity.
Lalla (c 720-790 AD) followed Aryabhata but in fact disagreed with much of his astronomical work. Of note was his use of Aryabhata's improved approximation of to the fourth decimal place. Lalla also composed a commentary on Brahmagupta's Khandakhadyaka.
Govindasvami (c 800-860 AD) his most important work was a commentary on Bhaskara I's astronomical work Mahabhaskariya, he also considered Aryabhata's sine tables and constructed a table which led to improved values.
Sankara Narayana (c 840-900 AD) wrote a commentary on Bhaskara I's work Laghubhaskariya (which in turn was based on the work of Aryabhata). Of note is his work on solving first order indeterminate equations, and also his use of the alternate 'katapayadi' numeration system (as well as Sanskrit place value numerals)