MacTutor logo MacTutor

Graham Higman

Quick Info

Born
19 January 1917
Louth, Lincolnshire, England
Died
8 April 2008
Oxford, England
Summary
Graham Higman was an English mathematician who is known for his outstanding work in all aspects of the theory of groups.
Thumbnail of Graham Higman
View six larger pictures

Biography

Graham Higman was the son of the Reverend Joseph Higman (1876-1954) and Susan Mary Ethel Ellis (1885-1951). Joseph Higman, the son of a farmer born in Roche, Cornwell on 28 April 1876, had left school and was working as the clerk to a mining engineer at age fourteen in 1891. He became a United Methodist Minister in 1902 and, in 1909, married Susan Mary Ethel Ellis. Susan, born in St Keverne, Cornwall on 10 November 1885, was the daughter of a Bible Christian Minister of Religion. We note that the Bible Christian Church was a denomination of the Methodist Church. The first of Joseph and Susan Higman's children, Woodman Francis Higman was born in January 1911 but died in June of that year. Bryan Higman was born in Louth, Lincolnshire on 18 November 1914, Graham Higman, the subject of this biography, was born on 19 January 1917 and Graham's younger brother, Noel Higman, was born on 20 December 1918 in West Ham, London. Of course, with the strong family involvement with the Methodist Church, Graham was brought up in the Methodist tradition; the Methodist Church would form a major part of his whole life.

The family moved a number of times while Graham was growing up. In 1918 the family moved to West Ham, London where they remained until 1924. In that year they moved to Long Eaton, Derbyshire where they remained until 1929. Graham entered Sutton Secondary School for Boys in Plymouth in 1929 when the family moved to that city. This school, first opened as the Regent Street Higher Grade School in 1897, had been reorganised under the name Sutton Secondary School for Boys on 13 September 1926. The headmaster from 1926 to 1935 was Alexander L Strachan. Higman said in the interview [11]:-
I first became interested in mathematics in general when I was in school. In the same way as most school children choose a subject, it was the subject I was best at.
In his final year at Sutton Secondary School, in 1934 Higman won a natural sciences scholarship to study at Balliol College Oxford. He chose Balliol College because that was the College where his elder brother Bryan had studied but, since his elder brother had read chemistry, Graham decided he had to be different in some respect and so, despite holding a natural sciences scholarship, he chose to read mathematics.

Higman's tutor was Henry Whitehead and it took a while before he realised that Higman was a natural pure mathematician since most students on a natural sciences scholarship would only take mathematics courses to support their science studies. Following a suggestion by Whitehead, Higman was a co-founder the 'Invariant Society' (an Oxford undergraduate mathematical society to "promote interest in all branches of Mathematics") in 1936. Higman was in Whitehead's office when the suggestion was made and, looking at the book shelves, he spotted Oswald Veblen's Invariants of Quadratic Differential Forms. He immediately proposed the name 'Invariant Society'. The first speaker was G H Hardy who addressed the Invariant Society in the Hilary Term of 1936 on Round Numbers. Hardy called a number 'round' if it is the product of a considerable number of comparatively small factors. Thus 1200=24.3.521200 = 2^{4}. 3. 5^{2} would be called round.

While studying as an undergraduate Higman became a fully accredited Methodist Local Preacher in 1936. Marston Conder writes in [3]:-
It has been reported that Graham's Methodism was far from old-fashioned, and that he welded his faith to an understanding of evolution, and thought deeply about the role of the after-death in religion, which he described as "one of the murkier areas of Christianity."
After taking special topic courses on group theory and differential geometry, Higman received an MA in 1938. After graduating he continued to study for his doctorate at Oxford. His doctoral research was supervised by the topologist Henry Whitehead and in [11] Higman explained how he became a group theorist despite having a topologist as advisor:-
When I was an undergraduate I was interested in several branches of mathematics. When I became a research student under Henry Whitehead, who was of course a topologist, he put me on to a problem in group theory with the intention that it should be applied later on in topology. I got as far as the group theory but I got stuck there so in a way you could say that I am a failed topologist and that's why I'm a group theorist.
He was awarded a DPhil. for his thesis The units of group-rings in 1941. In this work, among other results, he classified group rings over the rational numbers without non-trivial units. He had submitted the paper The units of group-rings to the Proceedings of the London Mathematical Society on 16 February 1939. In it he writes:-
I should like to thank Mr Whitehead for many helpful suggestions and much good advice that he has given me, both in the investigation of these problems and in the writing of this paper.
After his doctoral studies Higman spent a year at the University of Cambridge where he was strongly influenced by Philip Hall. He also met Max Newman in Cambridge and Newman's interest in the interaction between group theory and logic had a lasting influence on him. By this time World War II had started and Higman had signed up as a conscientious objector. However he did war service in the Meteorological Office from 1940 to 1946. He began this work, which did not involve using any mathematical skills or knowledge, in Lincolnshire, also spending time in Northern Ireland and Gibraltar.

In 1941 Higman married Ivah May Treleaven in Cockermouth, Cumberland. Ivah was born on the 2 May 1917 in Portsmouth to the Methodist Minister Woodman Treleaven and his wife Mabel Helen Cassell. Graham and Ivah Higman had five sons and a daughter.

At the end of the war Higman decided to apply for a permanent post in the Meteorological Office but, after being asked at an interview why he had not chosen to enter the academic world, he turned down the offered post and looked for an academic career. The first offer of such a post came from the University of Durham but, preferring to go to Manchester to be with Max Newman, he turned down Durham before receiving any offer from Manchester. The offer from Manchester did come and, in 1946, Higman was appointed as a lecturer in mathematics at the University of Manchester.

When he first arrived at Manchester Higman worked with Max Newman. He had not undertaken research on mathematics during the war years and, surprisingly since he claimed to be a "failed topologist", his first paper submitted on 26 March 1947 was a topology paper, namely The compacting of topological spaces. His next paper, A theorem on linkages, submitted on 27 September 1947, is also a topology paper. His first group theory paper was Note on a theorem of R Baer (1949) which has the following Abstract:-
It is trivial that a group all of whose elements except the identity have order two is Abelian; and F Levi and B L van der Waerden have shown that a group all of whose elements except the identity have order three has class less than or equal to three. On the other hand, R Baer has shown that if the fact that all the elements of a group have orders dividing n implies a limitation on the class of the group, then n is a prime. The object of the present note is to extend this result by showing that if M is a fixed integer there are at most a finite number of prime powers n other than primes, such that the fact that all the elements of a group have orders dividing n implies a limitation on the class of its Mth derived group.
Walter Ledermann was, like Higman, appointed to Manchester in 1946 and then Bernhard Neumann arrived in 1948. Higman and Neumann collaborated proving a number of very significant results which we comment on below. Despite the large amount of activity in group theory which was going on in Manchester, Higman was ambitious and began to apply for professorships. It is not surprising that at this early stage in his career he was unsuccessful, but Henry Whitehead encouraged him to return to Oxford rather than to seek a chair at a second rate place. He did so in 1955 being appointed as a Lecturer in Mathematics in Oxford and then, very soon after, he was promoted to Reader in Mathematics. In 1958 he was honoured with election as a Fellow of the Royal Society of London and, in the same year, he became a Senior Research fellow at his old Oxford College, Balliol College.

Higman was appointed Waynflete Professor of Pure Mathematics at Oxford in October 1960 and, at the same time, he was elected a Fellow of Magdalen College Oxford. He held these positions until he retired in 1984. Immediately after he retired from Oxford, Higman went to the United States where he was George A Miller visiting professor at the University of Illinois for the two years from 1984 to 1986.

Higman is known for his outstanding work in all aspects of the theory of groups. He published on units in group rings, the subject of his doctoral thesis, in 1940 then there was a break in his publication record during the time he worked in the Meteorological Office. We noted above that his 1948 papers are on somewhat different topics, being on topological spaces and linkages. They show the influences of Henry Whitehead and, to a lesser extent, Max Newman.

In 1949 Higman published one of several major pieces of work which stand as a landmark in the development of group theory. His paper Embedding theorems for groups written jointly with both Bernhard Neumann, who, as we noted, was a colleague of Graham Higman's at Manchester at that time, and with Hanna Neumann, introduces the now standard group construction of HNN extensions (Higman-Neumann-Neumann extensions).

Higman published further important papers in 1951 when he gave an example of a finitely presented group which is isomorphic to a proper factor of itself, and Higman's famous example of a finitely generated infinite simple group. Other work which he did around this time was on unrestricted free products and topological groups.

Two further papers written jointly with Bernhard Neumann were Groups as groupoids with one law and On two questions of Ito. After working on finitely generated nilpotent groups and infinite simple permutation groups, Higman, together with Philip Hall, produced another of his landmark papers in 1956 On the p-length of p-soluble groups and reduction theorems for Burnside's problem. It is this paper which introduced many important ideas but the most significant result was a reduction theorem for the restricted Burnside problem which essentially reduced the problem to looking only at groups of prime power exponent. This result plays a vital part in Zelmanov's positive solution to the restricted Burnside problem in the early 1990s. Higman made other contributions to the Burnside problem with a paper on groups of exponent 5.

Perhaps his most surprising result, and one of his most influential, appeared in Subgroups of finitely presented groups published in the Proceedings of the Royal Society in 1961. There he proved:-
Any finitely generated group can be embedded in a finitely presented group if and only if it is recursively presented.
As a corollary to this theorem Higman proved the existence of a universal finitely presented group containing every finitely presented group as a subgroup. Another application in the paper produced a new example of a finitely presented group with unsolvable word problem.

Higman also worked on topics such as: varieties of groups; enumerating pp-groups; and Lie ring methods for finite nilpotent groups. Then in 1967 he became interested in the sporadic finite simple groups being discovered at this time and played an important role in constructing certain of these groups from a knowledge of their character tables. He published papers on the Higman-Sims simple group (named after D G Higman and not Graham Higman) and on Janko's group of order 50232960. I [EFR] attended a lecture course which he gave at Oxford on this topic in the 1960s. It was a very exciting course, presenting results which he had only just proved, and often, it seemed, results he worked out on the blackboard during the lectures. In September 1969 he organised a two-week instructional conference, supported by the London Mathematical Society and NATO, on 'Finite Simple Groups'. You can see a picture of the participants at THIS LINK.

Together with Bill Boone, Higman worked on the word problem and together they wrote two papers on the algebraic structure of groups with soluble word problem and with soluble order problem. [A finitely generated group has soluble order problem if given any word in the generators there is an algorithm to determine its order.]

In the interview [11] he was asked why he thought the study of group theory is important. He gave the following reply:-
Well, in the first place, like many other research mathematicians, I do what I do, not only because I think it is important but also because I think it's interesting. The problems one has to deal with in group theory are challenging, they are intellectually difficult. When one has got into a problem it's not so much the question of how much it has an application to the real world that concerns you, it's a question of exercising your mind, exercising the control the mind has over the things it understands. Of course it is true that group theory has applications in the sciences. Perhaps we should say for the benefit of most of the people who might be listening to us and have no idea what group theory is, that group theory is in fact the study of symmetry. What a group theorist is concerned with is the possible amounts of symmetry that an object can have, symmetry in the abstract is our study and because everything has some degree of symmetry and because a physical scientist for instance who is studying a problem finds it easier to deal with it if he takes symmetry into account he needs to know what kinds of symmetries there are and therefore needs to know the results of group theory. It is in that way that group theory acts as a servant to other sciences as well as being an interesting subject in its own right.
Marston Conder, one of Higman's research students in the latter part of the 1970s, writes in [3] about Higman as a thesis advisor:-
As Waynflete professor, Graham had numerous doctoral students. His approach to supervision was not unusual for the time, but was certainly different from current expectations. He disliked scheduling regular meetings, and preferred that his students would attend colloquia and advanced classes, not just those he conducted himself, appear for tea in the Mathematical Institute's common room on a regular basis (to engage in mathematical conversations), and come to see him only when they had something important to say or ask; and when that happened, he would put aside his own work in order to help the student, offering many ideas and explanations (usually sketched on a board), and yet he would not seek credit for those ideas, let alone eventual joint authorship. ... Graham's approach helped to develop a large degree of independence and self-reliance in most (but not all) of his students. ... Sadly, a small number of students (and a few colleagues) found him intimidating, possibly because of his high academic standing and reputation, and some needed quite a lot of help, or a change of topic or supervisor.
Michael Collins writes in [1] about some of Higman's life other than mathematics:-
Relaxation came from bird-watching, and Higman would often arrive in the morning at the Mathematical Institute in a shabby raincoat, binoculars around his neck, to report on the latest sighting. He remained active in the Wesley Memorial Church in Oxford with a particular love for Wesley's hymns, and he participated in one of its book reading groups until about three years ago. For many years, too, he was involved with the Samaritans.
I [EFR] can also report on his love of walking. Once when he was coming to St Andrews to give a seminar, we offered to meet his train at Leuchars, about 5 miles from the Mathematical Institute. Thanking us for the offer, he said he preferred to walk (there is a cycle path most of the way). When he arrived at the Institute he certainly looked the worse for wear with mud all over his trousers. He gave an excellent seminar but I'm sure it was the only seminar I ever attended where the speaker was covered in mud.

Higman retired in 1984 and the Oxford Mathematical Institute named one of their seminar rooms the 'Higman Room' and hung this portrait painted by Norman Blamey.


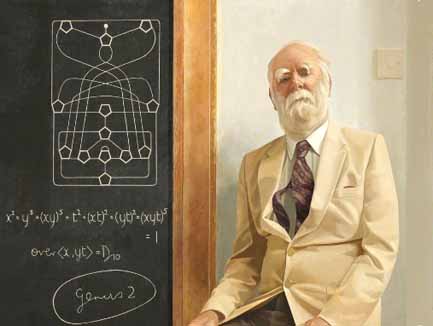
Click the picture to see a larger version

Higman did not like getting his photograph taken and often remarked that he disliked all photos of him but that he really liked the Norman Blamey portrait.

Ivah Higman died in Headington, Oxford, on 31 March 1981. Higman, the Methodist Local Preacher, gave the funeral address himself. He delivered the address in his usual style, without notes. He continued to undertake research and attend conferences. For example he was at the University of Illinois Urbana-Champaign for around two years in 1986-87, attended a conference in Singapore in June 1987 (I [EFR] was at that conference and attended Graham's lecture Some countably free groups), then he spent three weeks in Pakistan in July 1987. It was at this time that the interview [11] took place. He then spent ten days birdwatching in the highly mountainous Gilgit-Baltistan region of Pakistan before returning to England.

He published the book (co-authored with Elizabeth Scott) Existentially closed groups in 1988. Kenneth Hickin begins his review [7] with the following sentences:-
This volume grew out of lectures given by Higman at Oxford in 1983 and 1984 as recorded and amended by Scott. It is not a comprehensive work on existentially closed groups but rather contains an ample selection of topics written at an easily accessible graduate level. Both algebraic and model-theoretic aspects of existentially closed groups are highlighted.
Later in the review Hickin explains [7]:-
The subject of existentially closed groups currently occupies a special place in the model theory and logic of algebraic systems. This is due to a number of convergent factors, not the least of which is that this subject performs a type of wedding between recursion theory (the foundation of mathematical logic) on the one hand and group theory (the foundation of the analysis of mathematical structure) on the other. In another sense, it and related topics in other systems provide a testing ground for the classificatory concepts of model theory. Existentially closed groups provide an exemplary case in which powerful techniques are available to explore the details and potentials of logical complexity in a class of systems well known for their intrinsic beauty.
One of Higman's last papers is On a Certain Infinite Permutation Group (1990). The first paragraph is typically Higman and we give it here:-
This paper can, I think, best be considered as a sort of five finger exercise. In it we polish the techniques from a corner of group theory by using them to investigate the structure of a particular infinite permutation group. However, the group that we consider though particular is a fairly natural one, and while the results have a familiar general shape they include one detail which to me was quite unexpected. These facts perhaps constitute a challenge to place the results in a more general context; if so I make no attempt to meet it.
His final paper was Transversals and conjugacy in the group of recursive permutations which was published in the Proceedings of the 'Third International Conference on the Theory of Groups and Related Topics' held at the Australian National University, Canberra, 25-29 September 1989. His physical health deteriorated, but he remained mentally sharp. He spent the last years of his life in a nursing home but was able to make a brief appearance at the two-day conference The Hall-Higman theorems: fifty years on which was held at the Oxford Mathematical Institute in January 2007, to mark Higman's 90th birthday [6]:-
Participants felt themselves privileged when Graham Higman decided only the day before that he would attend both for the opening and for some of the lectures.
Higman has received many honours for his outstanding work in group theory. He was awarded the Berwick Prize from the London Mathematical Society in 1962 and the De Morgan Medal from that Society in 1974. He served the London Mathematical Society as its 52nd president from 1965 to 1967. In addition to his election as a Fellow of the Royal Society in 1958, the Royal Society awarded him its Sylvester Medal in 1979. He received a number of honorary degrees.

Finally let us give brief information about two members of the Higman family. Graham Higman's brother, Bryan Higman (1914-1991), studied chemistry at Balliol College Oxford, served in the air force during World War II teaching ballistics, and became a lecturer in Chemistry, then reader in Computer Science at the University of London, and finally a professor at the University of Lancaster. He published books such as Applied Group-theoretic and Matrix Methods (1964), A Comparative Study of Programming Languages (1967) and Foundation course in computer science (1975).

Graham Higman's son, Roger Higman, works for the Network of Wellbeing and Friends of the Earth [15]:-
Roger joined the Network of Wellbeing team in late 2014 to take on a leading role in developing our strategy. Roger has over 25 years' experience of campaigning mainly at Friends of the Earth, including locally, nationally and internationally on issues as diverse as climate change, biodiversity, resource use and economics. Roger is also a Director of the Flameworks Creative Arts Facility in Plymouth, where he lives with his partner, Karen and her three daughters. He is at his happiest exploring the countryside with Karen or working his allotment with his brother, Joe.
Other Mathematicians born in England
A Poster of Graham Higman

References (show)

  1. M Collins, Professor Graham Higman: Leading group theorist, The Independent (8 May 2008).
  2. M Collins, Professor Graham Higman, FRS, Oxford Mathematical Institute Newsletter 7 (2009), 2.
    https://www.maths.ox.ac.uk/system/files/legacy/3277/newsletter_0509_0.pdf
  3. M D E Conder, Graham Higman. 19 January 1917-8 April 2008, Biogr. Mems Fell. R. Soc. 73 (2022), 277-290.
  4. Graham Higman: Mathematician, Prabook.
    https://prabook.com/web/graham.higman/2318777
  5. Graham Higman, Institute for Advanced Studies.
    https://www.ias.edu/scholars/graham-higman
  6. Graham Higman at 90, Oxford Mathematical Newsletter (5) (2007), 7.
  7. K Hickin, Review: Existentially closed groups, by Graham Higman and Elizabeth Scott, Bull. Amer. Math. Soc. 23 (1) (1990), 242-249.
  8. Higman, Graham, A Dictionary of Methodism.
    https://dmbi.online/index.php?do=app.entry&id=3901
  9. Mathematics at Oxford: Dr Graham Higman, F.R.S., Nature 187 (1960), 830.
  10. S Oakes, A Pears and A Rice, The book of presidents, 1865-1965 (The London Mathematical Society, 2005).
  11. Professor Graham Higman, Interviewer Professor Qaiser Mushtaq, YouTube (22 January 2011).
    https://www.youtube.com/watch?v=gCuVT12f6Y8
  12. Professor Graham Higman, The Telegraph (26 May 2008).
  13. Obituaries, Professor Graham Higman, Balliol College and Magdalen College, Oxford University Gazette (17 April 2008).
  14. A Rice and R Wilson, Looking back: Graham Higman, European Math Soc Newsletter 41 (Sept 2001) 12-13.
  15. Roger Higman, Network of Wellbeing.
    https://networkofwellbeing.org/about/our-team/roger-higman/
  16. R Sandling, Graham Higman's thesis 'Units in group rings', in Integral representations and applications, Oberwolfach, 1980 (Berlin-New York, 1981), 93-116.

Additional Resources (show)

Honours (show)

Cross-references (show)

Written by J J O'Connor and E F Robertson
Last Update September 2001