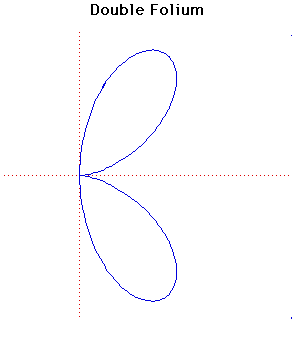Curves

Double Folium

Description

The general form of the folium is given by the formula

$(x^{2}+y^{2})(y^{2}+x(x+b)) = 4axy^{2}$

or, in polar coordinates

$r = -b \cos\theta + 4a \cos\theta \sin^{2}\theta$.

The word folium means leaf-shaped.

There are three special forms of the folium, the simple folium, the double folium and the trifolium. These correspond to the cases

$b = 4a, b = 0, b = a$

respectively in the formula for the general form.

The graph plotted above is the double folium. There are separate entries for the simple folium and the trifolium.

The double folium is the pedal curve of the tricuspoid where the pedal point is mid-point of one of the three curved sides.

Associated Curves

Definitions of the Associated curves

None

Evolute

Involute 1

Involute 2

Inverse curve wrt origin

Inverse wrt another circle

Pedal curve wrt origin

Pedal wrt another point

Negative pedal curve wrt origin

Negative pedal wrt another point

Caustic wrt horizontal rays

Caustic curve wrt another point