MacTutor logo MacTutor

Curves

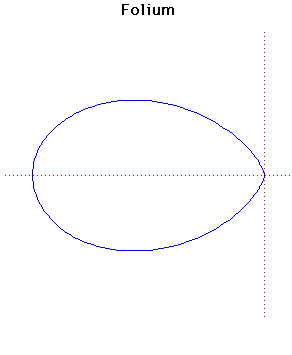
Folium

Main
Cartesian equation:
(x2+y2)(y2+x(x+b))=4axy2(x^{2} + y^{2})(y^{2} + x(x + b)) = 4axy^{2}
Polar equation:
r=−bcos⁡θ+4acos⁡θsin⁡2θr = -b \cos \theta + 4a \cos \theta \sin^{2} \theta

View the interactive version of this curve.

Description


The general form of the folium is given by the formula above. The word folium means leaf-shaped.

This curve was studied by Kepler in 1609 and Viviani in 1647.

There are three special forms of the folium, the simple folium, the double folium and the trifolium. These correspond to the cases
b=4a,b=0,b=ab = 4a, b = 0, b = a
respectively in the formula above.

The graph plotted above is the simple folium. There are separate entries for the double folium and the trifolium.

The simple folium is the pedal curve of the tricuspoid where the pedal point is one of the cusps.

Other Web site:

MathCurve

Associated Curves

Definitions of the Associated curves

  • Evolute
  • Involute 1
  • Involute 2
  • Inverse curve wrt origin
  • Inverse wrt another circle
  • Pedal curve wrt origin
  • Pedal wrt another point
  • Negative pedal curve wrt origin
  • Negative pedal wrt another point
  • Caustic wrt horizontal rays
  • Caustic curve wrt another point