Curves

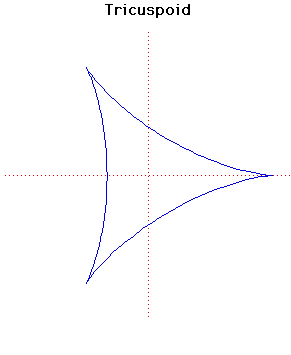
Tricuspoid

Description

The tricuspoid or deltoid was first considered by Euler in 1745 in connection with an optical problem. It was also investigated by Steiner in 1856 and is sometimes called Steiner's hypocycloid.

The length of the tangent to the tricuspoid, measured between the two points $P, Q$ in which it cuts the curve again is constant and equal to $4a$. If you draw tangents at $P$ and $Q$ they are at right angles.

The length of the curve is $16a$ and the area it encloses is $2\pi a^{2}$.

In the parametric form the cusps occur at $t = 0 , \large\frac{2\pi}{3}\normalsize$ and $\large\frac{4\pi}{3}\normalsize$. Notice the similarity between the parametric form of the tricuspoid and the parametric form of the cardioid.

The pedal of the tricuspoid, where the pedal point is the cusp, is a simple folium. The pedal, where the pedal point is the vertex, is a double folium. If the pedal point is on the inscribed equilateral triangle then the pedal is a trifolium.

The caustic of the tricuspoid, where the rays are parallel and in any direction, is an astroid.

Other Web site:

Xah Lee

Associated Curves

Definitions of the Associated curves

Evolute

Involute 1

Involute 2

Inverse curve wrt origin

Inverse wrt another circle

Pedal curve wrt origin

Pedal wrt another point

Negative pedal curve wrt origin

Negative pedal wrt another point

Caustic wrt horizontal rays

Caustic curve wrt another point