Curves
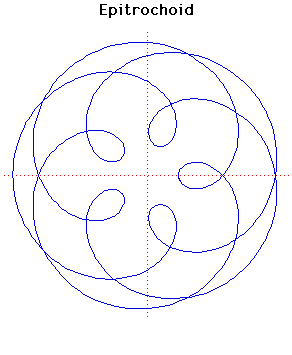
Epitrochoid
Description
There are four curves which are closely related. These are the epicycloid, the epitrochoid, the hypocycloid and the hypotrochoid and they are traced by a point on a circle of radius which rolls round a fixed circle of radius .For the epitrochoid, an example of which is shown above, the circle of radius rolls on the outside of the circle of radius . The point is at distance from the centre of the circle of radius . For the example and (so goes inside the circle of radius ).
An example of an epitrochoid appears in Dürer's work Instruction in measurement with compasses and straight edge(1525). He called them spider lines because the lines he used to construct the curves looked like a spider.
These curves were studied by la Hire, Desargues, Leibniz, Newton and many others.
Other Web site:
Xah Lee