Curves
Epicycloid
Description
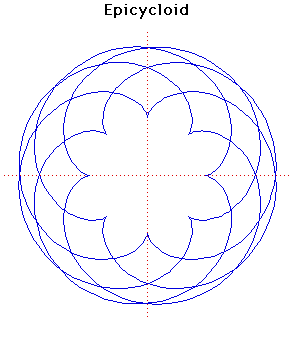
There are four curves which are closely related. These are the epicycloid, the epitrochoid, the hypocycloid and the hypotrochoid and they are traced by a point on a circle of radius which rolls round a fixed circle of radius .For the epicycloid, an example of which is shown above, the circle of radius rolls on the outside of the circle of radius . The point is on the circumference of the circle of radius . For the example drawn here and .
These curves were studied by Dürer (1525), Desargues (1640), Huygens (1679), Leibniz, Newton (1686), de L'Hôpital (1690), Jacob Bernoulli (1690), la Hire (1694), Johann Bernoulli (1695), Daniel Bernoulli (1725), Euler (1745, 1781).
Special cases are when a cardioid is obtained and when a nephroid is obtained.
If where is an integer, then the length of the epicycloid is and its area is .
The pedal curve, when the pedal point is the centre, is a rhodonea curve.
The evolute of an epicycloid is a similar epicycloid - look at the evolute of the epicycloid above to see it is a similar epicycloid but smaller in size.
Other Web site:
Xah Lee