Curves
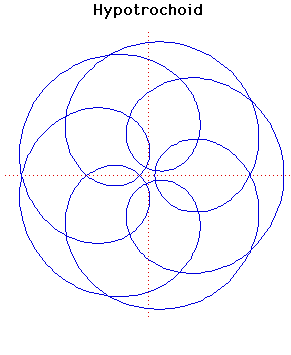
Hypotrochoid
Description
There are four curves which are closely related. These are the epicycloid, the epitrochoid, the hypocycloid and the hypotrochoid and they are traced by a point on a circle of radius which rolls round a fixed circle of radius .For the hypotrochoid, an example of which is shown above, the circle of radius rolls on the inside of the circle of radius . The point is at distance from the centre of the circle of radius . For this exampleand c = .
These curves were studied by la Hire, Desargues, Leibniz, Newton and many others.
Other Web site:
Xah Lee