An overview of Indian mathematics
It is without doubt that mathematics today owes a huge debt to the outstanding contributions made by Indian mathematicians over many hundreds of years. What is quite surprising is that there has been a reluctance to recognise this and one has to conclude that many famous historians of mathematics found what they expected to find, or perhaps even what they hoped to find, rather than to realise what was so clear in front of them.
We shall examine the contributions of Indian mathematics in this article, but before looking at this contribution in more detail we should say clearly that the "huge debt" is the beautiful number system invented by the Indians on which much of mathematical development has rested. Laplace put this with great clarity:-
Histories of Indian mathematics used to begin by describing the geometry contained in the Sulbasutras but research into the history of Indian mathematics has shown that the essentials of this geometry were older being contained in the altar constructions described in the Vedic mythology text the Shatapatha Brahmana and the Taittiriya Samhita. Also it has been shown that the study of mathematical astronomy in India goes back to at least the third millennium BC and mathematics and geometry must have existed to support this study in these ancient times.
The first mathematics which we shall describe in this article developed in the Indus valley. The earliest known urban Indian culture was first identified in 1921 at Harappa in the Punjab and then, one year later, at Mohenjo-daro, near the Indus River in the Sindh. Both these sites are now in Pakistan but this is still covered by our term "Indian mathematics" which, in this article, refers to mathematics developed in the Indian subcontinent. The Indus civilisation (or Harappan civilisation as it is sometimes known) was based in these two cities and also in over a hundred small towns and villages. It was a civilisation which began around 2500 BC and survived until 1700 BC or later. The people were literate and used a written script containing around 500 characters which some have claimed to have deciphered but, being far from clear that this is the case, much research remains to be done before a full appreciation of the mathematical achievements of this ancient civilisation can be fully assessed.
We often think of Egyptians and Babylonians as being the height of civilisation and of mathematical skills around the period of the Indus civilisation, yet V G Childe in New Light on the Most Ancient East (1952) wrote:-
It is unclear exactly what caused the decline in the Harappan civilisation. Historians have suggested four possible causes: a change in climatic patterns and a consequent agricultural crisis; a climatic disaster such flooding or severe drought; disease spread by epidemic; or the invasion of Indo-Aryans peoples from the north. The favourite theory used to be the last of the four, but recent opinions favour one of the first three. What is certainly true is that eventually the Indo-Aryans peoples from the north did spread over the region. This brings us to the earliest literary record of Indian culture, the Vedas which were composed in Vedic Sanskrit, between 1500 BC and 800 BC. At first these texts, consisting of hymns, spells, and ritual observations, were transmitted orally. Later the texts became written works for use of those practicing the Vedic religion.
The next mathematics of importance on the Indian subcontinent was associated with these religious texts. It consisted of the Sulbasutras which were appendices to the Vedas giving rules for constructing altars. They contained quite an amount of geometrical knowledge, but the mathematics was being developed, not for its own sake, but purely for practical religious purposes. The mathematics contained in the these texts is studied in some detail in the separate article on the Sulbasutras.
The main Sulbasutras were composed by Baudhayana (about 800 BC), Manava (about 750 BC), Apastamba (about 600 BC), and Katyayana (about 200 BC). These men were both priests and scholars but they were not mathematicians in the modern sense. Although we have no information on these men other than the texts they wrote, we have included them in our biographies of mathematicians. There is another scholar, who again was not a mathematician in the usual sense, who lived around this period. That was Panini who achieved remarkable results in his studies of Sanskrit grammar. Now one might reasonably ask what Sanskrit grammar has to do with mathematics. It certainly has something to do with modern theoretical computer science, for a mathematician or computer scientist working with formal language theory will recognise just how modern some of Panini's ideas are.
Before the end of the period of the Sulbasutras, around the middle of the third century BC, the Brahmi numerals had begun to appear.
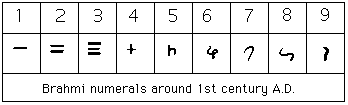
These are the earliest numerals which, after a multitude of changes, eventually developed into the numerals 1, 2, 3, 4, 5, 6, 7, 8, 9 used today. The development of numerals and place-valued number systems are studied in the article Indian numerals.
The Vedic religion with its sacrificial rites began to wane and other religions began to replace it. One of these was Jainism, a religion and philosophy which was founded in India around the 6th century BC. Although the period after the decline of the Vedic religion up to the time of Aryabhata I around 500 AD used to be considered as a dark period in Indian mathematics, recently it has been recognised as a time when many mathematical ideas were considered. In fact Aryabhata is now thought of as summarising the mathematical developments of the Jaina as well as beginning the next phase.
The main topics of Jaina mathematics in around 150 BC were: the theory of numbers, arithmetical operations, geometry, operations with fractions, simple equations, cubic equations, quartic equations, and permutations and combinations. More surprisingly the Jaina developed a theory of the infinite containing different levels of infinity, a primitive understanding of indices, and some notion of logarithms to base 2. One of the difficult problems facing historians of mathematics is deciding on the date of the Bakhshali manuscript. If this is a work which is indeed from 400 AD, or at any rate a copy of a work which was originally written at this time, then our understanding of the achievements of Jaina mathematics will be greatly enhanced. While there is so much uncertainty over the date, a topic discussed fully in our article on the Bakhshali manuscript, then we should avoid rewriting the history of the Jaina period in the light of the mathematics contained in this remarkable document.
You can see a separate article about Jaina mathematics at THIS LINK.
If the Vedic religion gave rise to a study of mathematics for constructing sacrificial altars, then it was Jaina cosmology which led to ideas of the infinite in Jaina mathematics. Later mathematical advances were often driven by the study of astronomy. Well perhaps it would be more accurate to say that astrology formed the driving force since it was that "science" which required accurate information about the planets and other heavenly bodies and so encouraged the development of mathematics. Religion too played a major role in astronomical investigations in India for accurate calendars had to be prepared to allow religious observances to occur at the correct times. Mathematics then was still an applied science in India for many centuries with mathematicians developing methods to solve practical problems.
Yavanesvara, in the second century AD, played an important role in popularising astrology when he translated a Greek astrology text dating from 120 BC. If he had made a literal translation it is doubtful whether it would have been of interest to more than a few academically minded people. He popularised the text, however, by resetting the whole work into Indian culture using Hindu images with the Indian caste system integrated into his text.
By about 500 AD the classical era of Indian mathematics began with the work of Aryabhata. His work was both a summary of Jaina mathematics and the beginning of new era for astronomy and mathematics. His ideas of astronomy were truly remarkable. He replaced the two demons Rahu, the Dhruva Rahu which causes the phases of the Moon and the Parva Rahu which causes an eclipse by covering the Moon or Sun or their light, with a modern theory of eclipses. He introduced trigonometry in order to make his astronomical calculations, based on the Greek epicycle theory, and he solved with integer solutions indeterminate equations which arose in astronomical theories.
Aryabhata headed a research centre for mathematics and astronomy at Kusumapura in the northeast of the Indian subcontinent. There a school studying his ideas grew up there but more than that, Aryabhata set the agenda for mathematical and astronomical research in India for many centuries to come. Another mathematical and astronomical centre was at Ujjain, also in the north of the Indian subcontinent, which grew up around the same time as Kusumapura. The most important of the mathematicians at this second centre was Varahamihira who also made important contributions to astronomy and trigonometry.
The main ideas of Jaina mathematics, particularly those relating to its cosmology with its passion for large finite numbers and infinite numbers, continued to flourish with scholars such as Yativrsabha. He was a contemporary of Varahamihira and of the slightly older Aryabhata. We should also note that the two schools at Kusumapura and Ujjain were involved in the continuing developments of the numerals and of place-valued number systems. The next figure of major importance at the Ujjain school was Brahmagupta near the beginning of the seventh century AD and he would make one of the most major contributions to the development of the numbers systems with his remarkable contributions on negative numbers and zero. It is a sobering thought that eight hundred years later European mathematics would be struggling to cope without the use of negative numbers and of zero.
These were certainly not Brahmagupta's only contributions to mathematics. Far from it for he made other major contributions in to the understanding of integer solutions to indeterminate equations and to interpolation formulas invented to aid the computation of sine tables.
The way that the contributions of these mathematicians were prompted by a study of methods in spherical astronomy is described in [25]:-
Now a "mathematical family" would have a library which contained the writing of the previous generations. These writings would most likely be commentaries on earlier works such as the Aryabhatiya of Aryabhata. Many of the commentaries would be commentaries on commentaries on commentaries etc. Mathematicians often wrote commentaries on their own work. They would not be aiming to provide texts to be used in educating people outside the family, nor would they be looking for innovative ideas in astronomy. Again religion was the key, for astronomy was considered to be of divine origin and each family would remain faithful to the revelations of the subject as presented by their gods. To seek fundamental changes would be unthinkable for in asking others to accept such changes would be essentially asking them to change religious belief. Nor do these men appear to have made astronomical observations in any systematic way. Some of the texts do claim that the computed data presented in them is in better agreement with observation than that of their predecessors but, despite this, there does not seem to have been a major observational programme set up. Paramesvara in the late fourteenth century appears to be one of the first Indian mathematicians to make systematic observations over many years.
Mathematics however was in a different position. It was only a tool used for making astronomical calculations. If one could produce innovative mathematical ideas then one could exhibit the truths of astronomy more easily. The mathematics therefore had to lead to the same answers as had been reached before but it was certainly good if it could achieve these more easily or with greater clarity. This meant that despite mathematics only being used as a computational tool for astronomy, the brilliant Indian scholars were encouraged by their culture to put their genius into advances in this topic.
A contemporary of Brahmagupta who headed the research centre at Ujjain was Bhaskara I who led the Asmaka school. This school would have the study of the works of Aryabhata as their main concern and certainly Bhaskara was commentator on the mathematics of Aryabhata. More than 100 years after Bhaskara lived the astronomer Lalla, another commentator on Aryabhata.
The ninth century saw mathematical progress with scholars such as Govindasvami, Mahavira, Prthudakasvami, Sankara, and Sridhara. Some of these such as Govindasvami and Sankara were commentators on the text of Bhaskara I while Mahavira was famed for his updating of Brahmagupta's book. This period saw developments in sine tables, solving equations, algebraic notation, quadratics, indeterminate equations, and improvements to the number systems. The agenda was still basically that set by Aryabhata and the topics being developed those in his work.
The main mathematicians of the tenth century in India were Aryabhata II and Vijayanandi, both adding to the understanding of sine tables and trigonometry to support their astronomical calculations. In the eleventh century Sripati and Brahmadeva were major figures but perhaps the most outstanding of all was Bhaskara II in the twelfth century. He worked on algebra, number systems, and astronomy. He wrote beautiful texts illustrated with mathematical problems, some of which we present in his biography, and he provided the best summary of the mathematics and astronomy of the classical period.
Bhaskara II may be considered the high point of Indian mathematics but at one time this was all that was known [26]:-
Some of the remarkable discoveries of the Kerala mathematicians are described in [26]. These include: a formula for the ecliptic; the Newton-Gauss interpolation formula; the formula for the sum of an infinite series; Lhuilier's formula for the circumradius of a cyclic quadrilateral. Of particular interest is the approximation to the value of which was the first to be made using a series. Madhava's result which gave a series for , translated into the language of modern mathematics, reads
The first person in modern times to realise that the mathematicians of Kerala had anticipated some of the results of the Europeans on the calculus by nearly 300 years was Charles Whish in 1835. Whish's publication in the Transactions of the Royal Asiatic Society of Great Britain and Ireland was essentially unnoticed by historians of mathematics. Only 100 years later in the 1940s did historians of mathematics look in detail at the works of Kerala's mathematicians and find that the remarkable claims made by Whish were essentially true. See for example [15]. Indeed the Kerala mathematicians had, as Whish wrote:-
Now we have presented the latter part of the history of Indian mathematics in an unlikely way. That there would be essentially no progress between the contributions of Bhaskara II and the innovations of Madhava, who was far more innovative than any other Indian mathematician producing a totally new perspective on mathematics, seems unlikely. Much more likely is that we are unaware of the contributions made over this 200 year period which must have provided the foundations on which Madhava built his theories.
Our understanding of the contributions of Indian mathematicians has changed markedly over the last few decades. Much more work needs to be done to further our understanding of the contributions of mathematicians whose work has sadly been lost, or perhaps even worse, been ignored. Indeed work is now being undertaken and we should soon have a better understanding of this important part of the history of mathematics.
We shall examine the contributions of Indian mathematics in this article, but before looking at this contribution in more detail we should say clearly that the "huge debt" is the beautiful number system invented by the Indians on which much of mathematical development has rested. Laplace put this with great clarity:-
The ingenious method of expressing every possible number using a set of ten symbols (each symbol having a place value and an absolute value) emerged in India. The idea seems so simple nowadays that its significance and profound importance is no longer appreciated. Its simplicity lies in the way it facilitated calculation and placed arithmetic foremost amongst useful inventions. the importance of this invention is more readily appreciated when one considers that it was beyond the two greatest men of Antiquity, Archimedes and Apollonius.We shall look briefly at the Indian development of the place-value decimal system of numbers later in this article and in somewhat more detail in the separate article Indian numerals. First, however, we go back to the first evidence of mathematics developing in India.
Histories of Indian mathematics used to begin by describing the geometry contained in the Sulbasutras but research into the history of Indian mathematics has shown that the essentials of this geometry were older being contained in the altar constructions described in the Vedic mythology text the Shatapatha Brahmana and the Taittiriya Samhita. Also it has been shown that the study of mathematical astronomy in India goes back to at least the third millennium BC and mathematics and geometry must have existed to support this study in these ancient times.
The first mathematics which we shall describe in this article developed in the Indus valley. The earliest known urban Indian culture was first identified in 1921 at Harappa in the Punjab and then, one year later, at Mohenjo-daro, near the Indus River in the Sindh. Both these sites are now in Pakistan but this is still covered by our term "Indian mathematics" which, in this article, refers to mathematics developed in the Indian subcontinent. The Indus civilisation (or Harappan civilisation as it is sometimes known) was based in these two cities and also in over a hundred small towns and villages. It was a civilisation which began around 2500 BC and survived until 1700 BC or later. The people were literate and used a written script containing around 500 characters which some have claimed to have deciphered but, being far from clear that this is the case, much research remains to be done before a full appreciation of the mathematical achievements of this ancient civilisation can be fully assessed.
We often think of Egyptians and Babylonians as being the height of civilisation and of mathematical skills around the period of the Indus civilisation, yet V G Childe in New Light on the Most Ancient East (1952) wrote:-
India confronts Egypt and Babylonia by the 3rd millennium with a thoroughly individual and independent civilisation of her own, technically the peer of the rest. And plainly it is deeply rooted in Indian soil. The Indus civilisation represents a very perfect adjustment of human life to a specific environment. And it has endured; it is already specifically Indian and forms the basis of modern Indian culture.We do know that the Harappans had adopted a uniform system of weights and measures. An analysis of the weights discovered suggests that they belong to two series both being decimal in nature with each decimal number multiplied and divided by two, giving for the main series ratios of 0.05, 0.1, 0.2, 0.5, 1, 2, 5, 10, 20, 50, 100, 200, and 500. Several scales for the measurement of length were also discovered during excavations. One was a decimal scale based on a unit of measurement of 1.32 inches (3.35 centimetres) which has been called the "Indus inch". Of course ten units is then 13.2 inches which is quite believable as the measure of a "foot". A similar measure based on the length of a foot is present in other parts of Asia and beyond. Another scale was discovered when a bronze rod was found which was marked in lengths of 0.367 inches. It is certainly surprising the accuracy with which these scales are marked. Now 100 units of this measure is 36.7 inches which is the measure of a stride. Measurements of the ruins of the buildings which have been excavated show that these units of length were accurately used by the Harappans in construction.
It is unclear exactly what caused the decline in the Harappan civilisation. Historians have suggested four possible causes: a change in climatic patterns and a consequent agricultural crisis; a climatic disaster such flooding or severe drought; disease spread by epidemic; or the invasion of Indo-Aryans peoples from the north. The favourite theory used to be the last of the four, but recent opinions favour one of the first three. What is certainly true is that eventually the Indo-Aryans peoples from the north did spread over the region. This brings us to the earliest literary record of Indian culture, the Vedas which were composed in Vedic Sanskrit, between 1500 BC and 800 BC. At first these texts, consisting of hymns, spells, and ritual observations, were transmitted orally. Later the texts became written works for use of those practicing the Vedic religion.
The next mathematics of importance on the Indian subcontinent was associated with these religious texts. It consisted of the Sulbasutras which were appendices to the Vedas giving rules for constructing altars. They contained quite an amount of geometrical knowledge, but the mathematics was being developed, not for its own sake, but purely for practical religious purposes. The mathematics contained in the these texts is studied in some detail in the separate article on the Sulbasutras.
The main Sulbasutras were composed by Baudhayana (about 800 BC), Manava (about 750 BC), Apastamba (about 600 BC), and Katyayana (about 200 BC). These men were both priests and scholars but they were not mathematicians in the modern sense. Although we have no information on these men other than the texts they wrote, we have included them in our biographies of mathematicians. There is another scholar, who again was not a mathematician in the usual sense, who lived around this period. That was Panini who achieved remarkable results in his studies of Sanskrit grammar. Now one might reasonably ask what Sanskrit grammar has to do with mathematics. It certainly has something to do with modern theoretical computer science, for a mathematician or computer scientist working with formal language theory will recognise just how modern some of Panini's ideas are.
Before the end of the period of the Sulbasutras, around the middle of the third century BC, the Brahmi numerals had begun to appear.

Here is one style of the Brahmi numerals:
These are the earliest numerals which, after a multitude of changes, eventually developed into the numerals 1, 2, 3, 4, 5, 6, 7, 8, 9 used today. The development of numerals and place-valued number systems are studied in the article Indian numerals.
The Vedic religion with its sacrificial rites began to wane and other religions began to replace it. One of these was Jainism, a religion and philosophy which was founded in India around the 6th century BC. Although the period after the decline of the Vedic religion up to the time of Aryabhata I around 500 AD used to be considered as a dark period in Indian mathematics, recently it has been recognised as a time when many mathematical ideas were considered. In fact Aryabhata is now thought of as summarising the mathematical developments of the Jaina as well as beginning the next phase.
The main topics of Jaina mathematics in around 150 BC were: the theory of numbers, arithmetical operations, geometry, operations with fractions, simple equations, cubic equations, quartic equations, and permutations and combinations. More surprisingly the Jaina developed a theory of the infinite containing different levels of infinity, a primitive understanding of indices, and some notion of logarithms to base 2. One of the difficult problems facing historians of mathematics is deciding on the date of the Bakhshali manuscript. If this is a work which is indeed from 400 AD, or at any rate a copy of a work which was originally written at this time, then our understanding of the achievements of Jaina mathematics will be greatly enhanced. While there is so much uncertainty over the date, a topic discussed fully in our article on the Bakhshali manuscript, then we should avoid rewriting the history of the Jaina period in the light of the mathematics contained in this remarkable document.
You can see a separate article about Jaina mathematics at THIS LINK.
If the Vedic religion gave rise to a study of mathematics for constructing sacrificial altars, then it was Jaina cosmology which led to ideas of the infinite in Jaina mathematics. Later mathematical advances were often driven by the study of astronomy. Well perhaps it would be more accurate to say that astrology formed the driving force since it was that "science" which required accurate information about the planets and other heavenly bodies and so encouraged the development of mathematics. Religion too played a major role in astronomical investigations in India for accurate calendars had to be prepared to allow religious observances to occur at the correct times. Mathematics then was still an applied science in India for many centuries with mathematicians developing methods to solve practical problems.
Yavanesvara, in the second century AD, played an important role in popularising astrology when he translated a Greek astrology text dating from 120 BC. If he had made a literal translation it is doubtful whether it would have been of interest to more than a few academically minded people. He popularised the text, however, by resetting the whole work into Indian culture using Hindu images with the Indian caste system integrated into his text.
By about 500 AD the classical era of Indian mathematics began with the work of Aryabhata. His work was both a summary of Jaina mathematics and the beginning of new era for astronomy and mathematics. His ideas of astronomy were truly remarkable. He replaced the two demons Rahu, the Dhruva Rahu which causes the phases of the Moon and the Parva Rahu which causes an eclipse by covering the Moon or Sun or their light, with a modern theory of eclipses. He introduced trigonometry in order to make his astronomical calculations, based on the Greek epicycle theory, and he solved with integer solutions indeterminate equations which arose in astronomical theories.
Aryabhata headed a research centre for mathematics and astronomy at Kusumapura in the northeast of the Indian subcontinent. There a school studying his ideas grew up there but more than that, Aryabhata set the agenda for mathematical and astronomical research in India for many centuries to come. Another mathematical and astronomical centre was at Ujjain, also in the north of the Indian subcontinent, which grew up around the same time as Kusumapura. The most important of the mathematicians at this second centre was Varahamihira who also made important contributions to astronomy and trigonometry.
The main ideas of Jaina mathematics, particularly those relating to its cosmology with its passion for large finite numbers and infinite numbers, continued to flourish with scholars such as Yativrsabha. He was a contemporary of Varahamihira and of the slightly older Aryabhata. We should also note that the two schools at Kusumapura and Ujjain were involved in the continuing developments of the numerals and of place-valued number systems. The next figure of major importance at the Ujjain school was Brahmagupta near the beginning of the seventh century AD and he would make one of the most major contributions to the development of the numbers systems with his remarkable contributions on negative numbers and zero. It is a sobering thought that eight hundred years later European mathematics would be struggling to cope without the use of negative numbers and of zero.
These were certainly not Brahmagupta's only contributions to mathematics. Far from it for he made other major contributions in to the understanding of integer solutions to indeterminate equations and to interpolation formulas invented to aid the computation of sine tables.
The way that the contributions of these mathematicians were prompted by a study of methods in spherical astronomy is described in [25]:-
The Hindu astronomers did not possess a general method for solving problems in spherical astronomy, unlike the Greeks who systematically followed the method of Ptolemy, based on the well-known theorem of Menelaus. But, by means of suitable constructions within the armillary sphere, they were able to reduce many of their problems to comparison of similar right-angled plane triangles. In addition to this device, they sometimes also used the theory of quadratic equations, or applied the method of successive approximations. ... Of the methods taught by Aryabhata and demonstrated by his scholiast Bhaskara I, some are based on comparison of similar right-angled plane triangles, and others are derived from inference. Brahmagupta is probably the earliest astronomer to have employed the theory of quadratic equations and the method of successive approximations to solving problems in spherical astronomy.Before continuing to describe the developments through the classical period we should explain the mechanisms which allowed mathematics to flourish in India during these centuries. The educational system in India at this time did not allow talented people with ability to receive training in mathematics or astronomy. Rather the whole educational system was family based. There were a number of families who carried the traditions of astrology, astronomy and mathematics forward by educating each new generation of the family in the skills which had been developed. We should also note that astronomy and mathematics developed on their own, separate for the development of other areas of knowledge.
Now a "mathematical family" would have a library which contained the writing of the previous generations. These writings would most likely be commentaries on earlier works such as the Aryabhatiya of Aryabhata. Many of the commentaries would be commentaries on commentaries on commentaries etc. Mathematicians often wrote commentaries on their own work. They would not be aiming to provide texts to be used in educating people outside the family, nor would they be looking for innovative ideas in astronomy. Again religion was the key, for astronomy was considered to be of divine origin and each family would remain faithful to the revelations of the subject as presented by their gods. To seek fundamental changes would be unthinkable for in asking others to accept such changes would be essentially asking them to change religious belief. Nor do these men appear to have made astronomical observations in any systematic way. Some of the texts do claim that the computed data presented in them is in better agreement with observation than that of their predecessors but, despite this, there does not seem to have been a major observational programme set up. Paramesvara in the late fourteenth century appears to be one of the first Indian mathematicians to make systematic observations over many years.
Mathematics however was in a different position. It was only a tool used for making astronomical calculations. If one could produce innovative mathematical ideas then one could exhibit the truths of astronomy more easily. The mathematics therefore had to lead to the same answers as had been reached before but it was certainly good if it could achieve these more easily or with greater clarity. This meant that despite mathematics only being used as a computational tool for astronomy, the brilliant Indian scholars were encouraged by their culture to put their genius into advances in this topic.
A contemporary of Brahmagupta who headed the research centre at Ujjain was Bhaskara I who led the Asmaka school. This school would have the study of the works of Aryabhata as their main concern and certainly Bhaskara was commentator on the mathematics of Aryabhata. More than 100 years after Bhaskara lived the astronomer Lalla, another commentator on Aryabhata.
The ninth century saw mathematical progress with scholars such as Govindasvami, Mahavira, Prthudakasvami, Sankara, and Sridhara. Some of these such as Govindasvami and Sankara were commentators on the text of Bhaskara I while Mahavira was famed for his updating of Brahmagupta's book. This period saw developments in sine tables, solving equations, algebraic notation, quadratics, indeterminate equations, and improvements to the number systems. The agenda was still basically that set by Aryabhata and the topics being developed those in his work.
The main mathematicians of the tenth century in India were Aryabhata II and Vijayanandi, both adding to the understanding of sine tables and trigonometry to support their astronomical calculations. In the eleventh century Sripati and Brahmadeva were major figures but perhaps the most outstanding of all was Bhaskara II in the twelfth century. He worked on algebra, number systems, and astronomy. He wrote beautiful texts illustrated with mathematical problems, some of which we present in his biography, and he provided the best summary of the mathematics and astronomy of the classical period.
Bhaskara II may be considered the high point of Indian mathematics but at one time this was all that was known [26]:-
For a long time Western scholars thought that Indians had not done any original work till the time of Bhaskara II. This is far from the truth. Nor has the growth of Indian mathematics stopped with Bhaskara II. Quite a few results of Indian mathematicians have been rediscovered by Europeans. For instance, the development of number theory, the theory of indeterminates infinite series expressions for sine, cosine and tangent, computational mathematics, etc.
Following Bhaskara II there was over 200 years before any other major contributions to mathematics were made on the Indian subcontinent. In fact for a long time it was thought that Bhaskara II represented the end of mathematical developments in the Indian subcontinent until modern times. However in the second half of the fourteenth century Mahendra Suri wrote the first Indian treatise on the astrolabe and Narayana wrote an important commentary on Bhaskara II, making important contributions to algebra and magic squares. The most remarkable contribution from this period, however, was by Madhava who invented Taylor series and rigorous mathematical analysis in some inspired contributions. Madhava was from Kerala and his work there inspired a school of followers such as Nilakantha and Jyesthadeva.
Some of the remarkable discoveries of the Kerala mathematicians are described in [26]. These include: a formula for the ecliptic; the Newton-Gauss interpolation formula; the formula for the sum of an infinite series; Lhuilier's formula for the circumradius of a cyclic quadrilateral. Of particular interest is the approximation to the value of which was the first to be made using a series. Madhava's result which gave a series for , translated into the language of modern mathematics, reads
This formula, as well as several others referred to above, were rediscovered by European mathematicians several centuries later. Madhava also gave other formulae for , one of which leads to the approximation 3.14159265359.
The first person in modern times to realise that the mathematicians of Kerala had anticipated some of the results of the Europeans on the calculus by nearly 300 years was Charles Whish in 1835. Whish's publication in the Transactions of the Royal Asiatic Society of Great Britain and Ireland was essentially unnoticed by historians of mathematics. Only 100 years later in the 1940s did historians of mathematics look in detail at the works of Kerala's mathematicians and find that the remarkable claims made by Whish were essentially true. See for example [15]. Indeed the Kerala mathematicians had, as Whish wrote:-
... laid the foundation for a complete system of fluxions ...and these works:-
... abound with fluxional forms and series to be found in no work of foreign countries.There were other major advances in Kerala at around this time. Citrabhanu was a sixteenth century mathematicians from Kerala who gave integer solutions to twenty-one types of systems of two algebraic equations. These types are all the possible pairs of equations of the following seven forms:
, and .
For each case, Citrabhanu gave an explanation and justification of his rule as well as an example. Some of his explanations are algebraic, while others are geometric. See [12] for more details.
Now we have presented the latter part of the history of Indian mathematics in an unlikely way. That there would be essentially no progress between the contributions of Bhaskara II and the innovations of Madhava, who was far more innovative than any other Indian mathematician producing a totally new perspective on mathematics, seems unlikely. Much more likely is that we are unaware of the contributions made over this 200 year period which must have provided the foundations on which Madhava built his theories.
Our understanding of the contributions of Indian mathematicians has changed markedly over the last few decades. Much more work needs to be done to further our understanding of the contributions of mathematicians whose work has sadly been lost, or perhaps even worse, been ignored. Indeed work is now being undertaken and we should soon have a better understanding of this important part of the history of mathematics.
References (show)
- 1. R Calinger, A conceptual history of mathematics (Upper Straddle River, N. J., 1999).
- L V Gurjar, Ancient Indian Mathematics and Vedha (Poona, 1947).
- G G Joseph, The crest of the peacock (London, 1991).
- R Mukherjee, Discovery of zero and its impact on Indian mathematics (Calcutta, 1991).
- C N Srinivasiengar, The history of ancient Indian mathematics (Calcutta, 1967).
- A I Volodarskii, Outlines of the history of medieval Indian mathematics (Russian) "Nauka" (Moscow, 1977).
- R C Gupta, A bibliography of selected Sanskrit and allied works on Indian mathematics and mathematical astronomy, Ganita Bharati 3 (3-4) (1981), 86-102.
- R C Gupta, A select bibliography of articles on ancient Indian mathematics, Math. Education 9 (4) (1975), B65-B75.
- R C Gupta, Glimpses of ancient Indian mathematics, Math. Education 11 (4) (1977), B80-B81.
- R C Gupta, Indian mathematics abroad up to the tenth century A.D., Ganita Bharati 4 (1-2) (1982), 10-16.
- R C Gupta, Indian mathematics and astronomy in the eleventh century Spain, Ganita Bharati 2 (3-4) (1980), 53-57.
- T Hayashi and T Kusuba, Twenty-one algebraic normal forms of Citrabhanu, Historia Math. 25 (1) (1998), 1-21.
- P Jha, Indian mathematics in the Dark Age, Ganita-Bharati 17 (1-4) (1995), 75-79.
- R Lal and R Prasad, Integral solutions of the equation Nx2+1 = y2 in ancient Indian mathematics (cakravala or the cyclic method), Ganita Bharati 15 (1-4) (1993), 41-54.
- K M Marar and C T Rajagopal, Gregory's series in the mathematical literature of Kerala, Math. Student 13 (1945), 92-98.
- V Mishra and S L Singh, Height and distance problems in ancient Indian mathematics, Ganita-Bharati 18 (1-4) (1996), 25-30.
- Kh R Muzafarova, Indian mathematics in Central Asia after al-Khwarizmi (Russian), in The great medieval scientist al-Khwarizmi (Tashkent, 1985), 240-247.
- I Oami, Ancient Indian mathematics (Japanese), Sugakushi Kenkyu No. 74 (1977), 31-43.
- S Parameswaran, Putumana Somayaji, Ganita Bharati 14 (1-4) (1992), 37-44.
- K R Rajagopalan, State of Indian mathematics in the southern region up to 10th century A.D., Ganita Bharati 4 (1-2) (1982), 78-82.
- C T Rajagopal and M S Rangachari, On medieval Kerala mathematics, Arch. Hist. Exact Sci. 35 (2) (1986), 91-99.
- R Rashed, Indian mathematics in Arabic, in The intersection of history and mathematics (Basel, 1994), 143-148.
- K V Sarma and S Hariharan, Yuktibhasa of Jyesthadeva : a book of rationales in Indian mathematics and astronomy - an analytical appraisal, Indian J. Hist. Sci. 26 (2) (1991), 185-207.
- R K Sarma, A note on the use of words for numbers in ancient Indian mathematics, Math. Education 7 (1973), A44-A45.
- K Shankar Shukla, Early Hindu methods in spherical astronomy, Ganita 19 (2) (1968), 49-72.
- T Thrivikraman, On the contribution of Kerala to mathematics in the late medieval and early modern periods, Math. Student 53 (1-4) (1985), 204-208
- A I Volodarskii, Indian mathematics and al-Biruni (Russian), in History and methodology of the natural sciences XX (Moscow, 1978), 49-57.
- A I Volodarskii, al-Khwarizmi and Indian mathematics (Russian), in The great medieval scientist al-Khwarizmi (Tashkent, 1985), 232-238.
Additional Resources (show)
Other websites about Indian mathematics:
Written by J J O'Connor and E F Robertson
Last Update November 2000
Last Update November 2000