MacTutor
Earliest Known Uses of Some of the Words of Mathematics (G)
The term GALOIS is used to refer to concepts found in the work of Evariste Galois or inspired by it: see his Oeuvres mathématiques. Most of the references are associated with one piece, the "Mémoire sur les conditions de résolubilité des équations par radicaux" (written in 1830 but first published in 1846 and comprising pp. 417ff. of the Ouevres. See also the entry GROUP.
The term GALOIS CONNECTION is due to Oystein Ore, "Galois Connexions," Trans. Amer. Math. Soc. 55 (1944), 493-513:
The object of this paper is to discuss a general type of correspondence between structures which I have called Galois connexions. These correspondences occur in a great variety of mathematical theories and in several instances in the theory of relations. ... The name is taken from the ordinary Galois theory of equations where the correspondence between subgroups and subfields represents a special correspondence of this type.The citation above was taken from a post by William C. Waterhouse. In another post, Phill Schultz writes:
The abstract notion of Galois Connection appears in Garrett Birkhoff, "Lattice Theory," Amer. Math. Soc. Coll. Pub., Vol 25, 1940. I believe this is the first such occurrence, since in later editions, Birkhoff refers to other publications, but they are all later than 1940. The attribution 'Galois Connection' is simply because classical Galois Theory, as developed by Artin in the 1930's, establishes a correspondence between subfields of an algebraic number field and subgroups of the group of automorphisms of that field which is a dual lattice isomorphism between the lattice of normal subfields and the lattice of normal subgroups. Birkhoff's idea is to replace the set of subfields and the set of subgroups by arbitrary posets. The normal subfields and subgroups correspond to lattices of 'closed' elements of the posets. The Galois Connection is then an order reversing correspondence between the posets which is a lattice dual isomorphism between the posets of 'closed' elements.GALOIS FIELD. See FIELD.
GALOIS GROUP. Galois'schen Gruppe is found in 1884 in Vorlesungen über das Ikosae by Felix Klein.
Galois group is found in 1887 in "Klein's Ikosaeder", American Journal of Mathematics. "The Galois group of an equation is the group of permutations of its roots which possesses the two properties—1st, that all corresponding rational functions of the roots are rationally known, and 2nd that it is the equation group for which this is true." At the end of the paper is a note reading "Cambridge, September, 1886."
[James A. Landau]
GALOIS THEORY. Théorie de Galois appears as a section heading in Camille Jordan's in Traité des substitutions et des équations algébriques (1870). Here the term refers to higher degree congruences [Margherita Barile].
Galois equation theory appears in Heinrich Weber, "Die allgemeinen Grundlagen der Galois'schen Gleichungstheorie," Mathematische Annalen, 43 (1893) [James A. Landau].
Galois theory is found in English in 1893 in the Bulletin of the New York Mathematical Society.
GAMBLER'S RUIN is the title of J. L. Coolidge's 1909 article in Annals of Mathematics, 10, 181-192. (David (2001)). However, the problem of finding the probability that when two men are gambling together the one will ruin the other goes back to Pascal. It appears as the fifth problem at the end of Huygens's De Ratiociniis in Ludo Aleae (1657) or, in English, The Value of All Chances ... (1714). The problem was treated by all the early writers in probability. See Hald (1990).
GAME THEORY. See THEORY OF GAMES.
GAMMA DISTRIBUTION. Although this distribution already had an important place in statistical theory in the early 20th century, the practice of calling it after the GAMMA FUNCTION on which it is based on became established in the journal literature in the 1930s and then in textbooks in the 1940s. Previously it was usually known by its designation in the Pearson family of curves, as a Type III distribution. [John Aldrich]
Gamma distribution is found in 1937 in Proceedings of the Cambridge Philosophical Society. [James A. Landau]
See also BETA DISTRIBUTION and PEARSON CURVES.
GAMMA FUNCTION. See BETA and GAMMA FUNCTIONS.
The term GASKET was coined by Benoit Mandelbrot. On page 131, [Chapter 14] of "The Fractal Geometry of Nature", Benoit Mandelbrot says:
Sierpinski gasket is the term I propose to denote the shape in Plate 141.And on page 142, Mandelbrot adds:
I call Sierpinski's curve a gasket, because of an alternative construction that relies upon cutting out 'tremas', a method used extensively in Chapter 8 and 31 to 35.The citation above was provided by Julio González Cabillón.
The word GAUGE (in gauge theory) was introduced as the German word maßstab by H. Weyl (1885-1955) in 1918 in Sitzungsber. d. Preuss. Akad. d. Wissensch. 30 May 475 [OED].
GAUSS'S THEOREM (divergence theorem). See DIVERGENCE THEOREM or GAUSS'S THEOREM.
GAUSS'S THEOREM (for solving certain binomial equations) is found in 1814 in A New Mathematical and Philosophical Dictionary by Peter Barlow: "GAUSS'S Theorem, is an expression used to denote a theorem invented by Gauss, professor of mathematics at Strasbourg, for the solution of certain binomial equations." [James A. Landau]
GAUSS-JORDAN METHOD. In Matrix Analysis and Applied Linear Algebra (2000), Carl D. Meyer writes, "Although there has been some confusion as to which Jordan should receive credit for this algorithm, it now seems clear that the method was in fact introduced by a geodesist named Wilhelm Jordan (1842-1899) and not by the more well known mathematician Marie Ennemond Camille Jordan (1838-1922), whose name is often mistakenly associated with the technique, but who is otherwise correctly credited with other important topics in matrix analysis, the JORDAN CANONICAL FORM being the most notable." Having identified the right Jordan is not the end of the problem, for A. S. Householder writes, in The Theory of Matrices in Numerical Analysis (1964, p. 141), "The Gauss-Jordan method, so-called seems to have been described first by Clasen (1888) [J. B. Clasen Ann. Soc. Sci. Bruxelles, (2), 12, 251-81.] .. Since it can be regarded as a modification of Gaussian elimination, the name of Gauss is properly applied, but that of Jordan seems to be due to an error, since the method was described only in the third edition of his Handbuch der Vermessungskunde, prepared after his death." These claims were examined by S. C. Althoen and R. McLaughlin (1987) "Gauss-Jordan Reduction: A Brief History," American Mathematical Monthly, 94, 130-142. They conclude that Householder was correct about Clasen and his 1888 publication but mistaken about Jordan who was very much alive when the third edition of his book appeared in 1888. They add that the "germ of the idea" was already present in the second edition of 1877. [This entry was contributed by John Aldrich.]
The name GAUSS-MARKOV THEOREM for the chief result on least squares and best linear unbiassed estimation in the linear (regression) model has a curious history. David (1998) refers to H. Scheffé's 1959 book Analysis of Variance for the first use of the phrase "Gauss-Markoff theorem" although a JSTOR search finds a few earlier occurrences including one from 1951 by E. L. Lehmann (Annals of Mathematical Statistics, 22, No. 4, p. 587). For some years previously the term "Markoff theorem" had been in use. It was popularised by J. Neyman who believed that this Russian contribution had been overlooked in the West — see his "On the Two Different Aspects of the Representative Method" (Journal of the Royal Statistical Society, 97, (1934), 558-625). The theorem is in chapter 7 of Markov's book probability theory, translated into German as Wahrscheinlichkeitsrechnung (1912). However R. L. Plackett (Biometrika, 36, (1949), 458-460) pointed out that Markov had done no more than Gauss nearly a century before in his Theoria combinationis observationum erroribus minimis obnoxiae (Theory of the combination of observations least subject to error) (1821/3). (In the nineteenth century the theorem was often referred to as "Gauss's second proof of the method of least squares" — the "first" being a Bayesian argument Gauss published in 1809 based on the normal distribution). Following Plackett, a few authors adopted the expression "Gauss theorem" but "Markov" was well-entrenched and the compromise "Gauss-Markov theorem" has become standard.
GAUSS-SEIDEL METHOD. The Gauss-Seidel method is certainly a misnomer, which is perhaps due to the influential textbook by Whittaker and Robinson.
According to Forsythe in 1953, the "cyclic single step process" was proposed by Nekrasov in 1885 and a block version of it by Mehmke in 1892.
In contrast to this, the methods of Gauss (1823) and Seidel (1874) proceed in a noncyclic manner, which treats the "worst component" first.
Gauss's criterion from which to pick the next unknown is the same as in Southwell's relaxation method, this is why Zurmühl in his 1950 textbook coined the term Gauss-Southwell method for it.
A. S. Householder wrote, "Forsythe has remarked that the Gauss-Seidel method was not known to Gauss and not recommended by Seidel."
A Google Books search by James A. Landau found Gauss-Seidel in 1948 in The theory of mathematical machines by Francis Joseph Murray: "at Present, there are a number of commercially available devices for solving simultaneous linear equations by the Gauss-Seidel method. We will discuss the Gauss-Seidel method and point out the restrictions."
This entry was contributed by Jan Peter Schäfermeyer. See GAUSSIAN ELIMINATION.
GAUSSIAN. The word Gaussian was used, not in a mathematical sense, in a letter of Jan. 17, 1839, from William Whewell to Quételet: "Airy has just put up his Gaussian apparatus..at Greenwich, including a Bifilar."
GAUSSIAN CURVATURE refers to a concept that Gauss introduced in his General Investigations of Curved Surfaces (Disquisitiones generales circa superficies curvas 1827) Werke Bd 4 217ff.
The first appearance in JSTOR (which covers the American journals that began publication in the late19th century) is in an article from 1900, which refers to "Gaussian curvature, as generalized by Kronecker" in a publication of 1869.
The term Gaussisches Krümmungsmass, i.e. Gaussian curvature, appears in 1869 in a paper by Lipschitz and a paper by Kronecker.
[Jan Peter Schäfermeyer contributed to this entry.]
GAUSSIAN CURVE. The term Gaussian applied to curve, law, distribution, etc. in probability and statistics commemorates Gauss's derivation of the normal curve from the principle of the arithmetic mean and his use of it in his first theory of least squares (1809). The derivation was new but not the distribution for Gauss knew it had been studied by De Moivre and Laplace. Gauss had only a passing interest in 'his' distribution for his second theory of least squares, which produced the Gauss-Markov theorem, avoided any use of it. However, in the 19th and early 20th centuries the first (normal-based) theory was more widely taught. See ARITHMETIC MEAN, GAUSS-MARKOV THEOREM, METHOD OF LEAST SQUARES.
The English word "Gaussian" was apparently first used in this context by Karl Pearson who was no enthusiast either for the name or for use of the distribution as a law of error: he did not think the curve should be named after Gauss, nor did he think that errors of measurement follow the curve.
Pearson used the phrase Gaussian curve of errors in a 1902 paper ("On the Mathematical Theory of Errors of Judgment, with Special Reference to the Personal Equation," Philosophical Transactions of the Royal Society of London, A, 198, pp. 235-299) where he argued that errors of measurement are not normally distributed. [James A. Landau]
OED2 indicates that Pearson used the phrases Gaussian distribution and Gaussian law in 1905 in "Das Fehlergesetz und Seine Verallgemeinerungen Durch Fechner und Pearson." A Rejoinder, Biometrika, 4, pp. 169-212: "Many of the other remedies which have been proposed to supplement what I venture to call the universally recognised inadequacy of the Gaussian law .. cannot .. effectively describe the chief deviations from the Gaussian distribution." (p. 189)
Pearson was replying to criticism in a German publication and "In writing for Germans I naturally spoke of the Gaussian curve." The use of "Gaussian" in textbooks is investigated in "Stigler's Law of Eponymy" (reprinted in S. M. Stigler (1999)). Stigler's earliest find is a German textbook from 1872.
Pearson (1905, p. 189n) also argued that Laplace had priority over Gauss in discovering the curve. However he thought that "On the whole my custom of terming the curve the Gauss-Laplacian or normal curve saves us from proportioning the merit of discovery between the two great astronomer mathematicians."
"Normal" (q.v.) was the dominant term in English language Statistics throughout the 20th century but "Gaussian" did quite well in Probability: e.g. "la loi de Gauss" in Paul Lévy Calcul des Probabilités (1925), "die Gaußsche Verteilung" in Richard von Mises Wahrscheinlichkeitsrechnung (1931) and "Gaussian distribution" in Norbert Wiener "The Homogeneous Chaos," American Journal of Mathematics, 60, (1938), pp. 897-936.
In an essay in the 1971 book Reconsidering Marijuana, Carl Sagan, using the pseudonym "Mr. X," wrote, "I can remember one occasion, taking a shower with my wife while high, in which I had an idea on the origins and invalidities of racism in terms of gaussian distribution curves. I wrote the curves in soap on the shower wall, and went to write the idea down."
The name GAUSSIAN ELIMINATION is a tribute to the scheme presented in section 13 of C. F. Gauss's Disquisitio de Elementis Ellipticis Palladis ex Oppositionibus Annorum 1803, 1804, 1807, 1808, 1809 (1811) in Werke vol 6. (See Application of the Method of Least Squares to the Elements of the Planet Pallas.) Gauss was describing a scheme for least squares calculations.
Gauss himself used the term eliminatio vulgaris in 1809 in Theoria motus corporum coelestium in sectionibus conicis solem ambientium, page 214.
The first one to have named the elimination method Gaussian was probably Bessel in an 1838 report on a surveying campaign in Eastern Prussia.
A complete account of how ordinary elimination became Gaussian elimination was given by Joseph Grcar.
Triangular elimination is found in 1961 in Numerical Methods for Science and Engineering. [Google print search by James A. Landau]
See METHOD OF LEAST SQUARES, GAUSS-JORDAN METHOD and PIVOT. See also the discussion of regression notation on the Earliest Uses of Symbols in Probability and Statistics page.
[Jan Peter Schäfermeyer contributed to this entry.]
GAUSSIAN INTEGER. G.H. Hardy and E.M. Wright refer to the "complex or 'Gaussian' integers," explaining, "The Gaussian integers were used first by Gauss in his researches on biquadratic reciprocity. See, in particular, his memoirs entitled "Theoria residuorum biquadraticorum," Werke II 67-148. (An Introduction to the Theory of Numbers, 1938.)
GAUSSIAN LOGARITHM is found in 1855 in Report of the Superintendent of the Coast Survey, Showing the Progress of the Survey during the year 1854: "The computation is greatly facilitated by the use of the Gaussian logarithms, which are now habitually inserted in the five-figure logarithm tables." [Google print search by James A. Landau]
The term GENERAL INTEGRAL is due to Lagrange (Kline, page 532).
GENERAL SOLUTION is found in 1820 in A Collection of Examples of the Applications of the Differential and Integral Calculus by George Peacock: "Lagrange has denominated the equation (3), the complete solution of the differential equation, to distinguish it from the general solution, which involves an arbitrary function; under this form alone the theory exemplified in p. 479, by which the particular solutions are deduced from the complete integrals, admits of application in the case of partial differential equations." [Google print search]
GENERAL TERM is found in 1791 in "A new method of investigating the sums of infinite series," by Rev. Samuel Vince, Philos. Trans. R. Soc.: "To find the sum of the infinite series whose general term is ..."
GENERALIZED FUNCTION. See DISTRIBUTION.
GENERALIZED INVERSE. In 1955 Roger Penrose published a paper describing "a generalization of the inverse of a non-singular matrix, as the unique solution of a certain set of equations." His paper "A Generalized Inverse for Matrices," Proc. Cambridge Philos. Soc.,
51, (1955), 406-413 provoked a comment from R. Rado, "Note on Generalized Inverses of Matrices" Proc. Cambridge Philos. Soc., 52, (1956), 600-1. Rado pointed out that the same operation "defined in a slightly different form, but easily shown to lead to the same matrix" had been introduced by E. H. Moore in 1920 and "systematically investigated" in 1935. The references are to "On the Reciprocal of the General Algebraic Matrix," Bulletin of the American Mathematical Society, 26, (1920) 394-5 and General Analysis, vol 1. Rado expressed the opinion, "It may possibly be the case that Moore's work on matrices is not as widely known as it deserves on account of the highly individual system of logical symbols he employs."
See MATRIX.
GENERALIZED LINEAR MODEL. The term and the associated theory appear in J. A. Nelder and R. W. M. Wedderburn "Generalized Linear Models," Journal of the Royal Statistical Society, A, 135, (1972), 370-384. "We develop a class of generalized linear models, which includes all the above examples [conventional linear models, probit, contingency tables, etc.], and we give a unified procedure for fitting them based on likelihood." p. 370. In 1975 the Royal Statistical Society's Working Party on Statistical Computing announced the "Generalised Linear Interactive Modelling" package, GLIM.
See also LINK FUNCTION and DEVIANCE
GENETIC DEFINITION was used by Christian Wolff (1679-1754) in Philosophia rat. sive logica (1728, 3rd ed. 1740) [Bernd Buldt].
Genetic definition was also used by Immanuel Kant (1724-1804).
Genetic definition was used in English in 1837-38 by the Scottish philosopher and logician William Hamilton (1788-1856) in Logic xxiv. (1866) II. 13: "In Genetic Definitions the defined subject is considered as in the progress to be, as becoming; the notion, therefore, has to be made, and is the result of the definition, which is consequently synthetic" [OED].
The term GENETIC METHOD (as opposed to "axiomatic method") was apparently introduced by David Hilbert (1862-1943), and its first use may be its appearance in the 1900 essay "Über den Zahlbegriff."
The term appears in English in Edward V. Huntington, "Complete Sets of Postulates for the Theory of Real Quantities," Transactions of the American Mathematical Society, July, 1903. Huntington popularized the use of the term.
Genetic method was used earlier in a different sense by Professor fuer hoehere Analysis und darstellende Geometrie Carl Reuschle (1847-1909), son of the German mathematician Carl Gustav Reuschle (1812-1875), in an article entitled "Constituententheorie, eine neue, principielle und genetische Methode zur Invariantentheorie" (1897) [Julio González Cabillón].
GENTZEN'S HAUPTSATZ. See HAUPTSATZ.
GENUS (referring to the number of holes in a surface). This term is due to A. Clebsch and is found in "über die Anwendung der Abelschen Funktionen in der Geometrie," Journal für Mathematik, 63, 189-243. This information is taken from a footnote in the paper "Development of the concept of homotopy," by Ria Vanden Eynde (in History of topology, pages 65-102. North-Holland, Amsterdam, 1999). [Dave Richeson]
The term GEODESIC was introduced in 1850 by Liouville and was taken from geodesy (Kline, page 886).
The term geodesic curvature is due to Pierre Ossian Bonnet (1819-1892), according to the University of St. Andrews website.
However, according to Jesper Lützen in The geometrization of analytical mechanics: a pioneering contribution by Joseph Liouville (ca. 1850), "Liouville defined the 'geodesic curvature' (the name is due to him)...."
GEOID was first used in German (geoide) in 1872 by Johann Benedict Listing (1808-1882) in Über unsere jetzige Kenntniss der Gestalt u. Grösze der Erde [OED].
GEOMETRIC DISTRIBUTION appears in W. Feller's Introduction to Probability Theory and its Applications volume 1 (1950). (David (2001)) While the name is relatively new, the concept goes back to the earliest days of probability. Hald (1990, p. 56) argues that one of the arguments Fermat put to Pascal (in 1654) is based on the geometric distribution. See PROBABILITY.
GEOMETRIC MEAN. The geometric mean is one of the three Pythagorean means. See MEAN.
The term geometrical mean is found in E. Halley "A Most Compendious and Facile Method for Constructing the Logarithms, Exemplified and Demonstrated from the Nature of Numbers, without any Regard to the Hyperbola, with a Speedy Method for Finding the Number from the Logarithm Given," Philosophical Transactions of the Royal Society of London, Vol. 19. (1695 - 1697), pp. 58-67. (JSTOR)
See also MEAN and LOGNORMAL.
The term GEOMETRIC PROGRESSION was used by Michael Stifel in 1543: "Divisio in Arethmeticis progressionibus respondet extractionibus radicum in progressionibus Geometricis" [James A. Landau].
Geometrical progression appears in English in 1557 in the Whetstone of Witte by Robert Recorde: "You can haue no progression Geometricalle, but it must be made either of square nombers, or els of like flattes" [OED].
Geometric progression is found in English in 1696 in A new theory of the earth, from its original, to the consummation of all things by William Whiston: "Which to how immense a Sum it would arise, those who know any thing of the nature of Geometrick Progressions will easily pronounce." [OED]
GEOMETRIC PROPORTION. In 1551 Robert Recorde wrote in Pathway to Knowledge: "Lycurgus .. is most praised for that he didde chaunge the state of their common wealthe frome the proportion Arithmeticall to a proportion geometricall" [OED].
Geometrical proportion appears in 1605 in Bacon, Adv. Learn.: "Is there not a true coincidence between commutative and distributive justice, and arithmetical and geometrical proportion?" [OED].
Geometrical proportion appears in 1656 in tr. Hobbes's Elem. Philos.: "If four Magnitudes be in Geometrical Proportion, they will also be Proportionals by Permutation, (that is, by transposing the Middle Terms)" [OED].
Geometric proportion appears in 1706 in Synopsis Palmariorum matheseos by William Jones: "In any Geometric Proportion, when the Antecedent is less than the Consequent, the Terms may be express'd by a and ar [OED].
GEOMETRIC SERIES is found in 1723 in A System of the Mathematics James Hodgson [Google print search, James A. Landau].
The term GEOMETRY was in use in the time of Plato and Aristotle, and "doubtless goes back at least to Thales," according to Smith (vol. 2, page 273). The Greek word γεωμετρια was formed from γη earth and μετρια measuring; transliteration produced the Latin geometria which became géométrie in French and thence geometry in English.
Smith also writes (vol. 2, page 273) that "Plato, Xenophon, and Herodotus use the word in some of its forms, but always to indicate surveying."
However, Michael N. Fried points out that Smith may not be entirely correct:
In the "Epinomis" (whose Platonic provenance is not completely clear), it is true that Plato refers to mensuration or surveying as 'gewmetria' (990d), but elsewhere Plato is very careful to distinguish between practical sciences concerning sensibles, such as surveying, and theoretical sciences, such as geometry. For instance, in the Philebus (of undisputed Platonic provenance), one has:Smith (vol. 2, page 273) writes, "Euclid did not call his treatise a geometry, probably because the term still related to land measure, but spoke of it merely as the Elements. Indeed, he did not employ the word 'geometry' at all, although it was in common use among Greek writers. When Euclid was translated into Latin in the 12th century, the Greek title was changed to the Latin form Elementa, but the word 'geometry' is often found in the title-page, first page, or last page of the early printed editions" (Smith vol. 2, page 273).
"SOCRATES: Then as between the calculating and measurement employed in building or commerce and the geometry and calculation practiced in philosophy-- well, should we say there is one sort of each, or should we recognize two sorts?
PROTARCHUS: On the strength of what has been said I should give my vote for there being two" (57a).
This distinction reoccurs in Proclus's neo-platonic commentary on Euclid's "Elements". There Proclus writes: "But others, like Geminus ... think of one part [of mathematics] as concerned with intelligibles only and of another as working with perceptibles and in contact with them... Of the mathematics that deals with intelligibles they posit arithmetic and geometry as the two primary and most authentic parts, while the mathematics that attends to sensibles contains six sciences: mechanics, astronomy, optics, geodesy, canonics, and calculation. Tactics they do not think it proper to call a part of mathematics, as others do, though they admit that it sometimes uses calculation... and sometimes geodesy, as in the division and measurement of encampments" (Friedlein, p.38).
Even Herodotus does not identify geometry and geodesy, but only claims that the origin of the former might have had it origin in the later (the Histories, II.109).
Geometry appears in English in 14th century manuscripts. An anonymous 14th century manuscript begins, "Nowe sues here a Tretis of Geometri wherby you may knowe the heghte, depnes, and the brede of mostwhat erthely thynges" (Smith vol. I, page 237). The OED shows another 14th century use.
The term GEOMETRY OF NUMBERS was coined by Hermann Minkowski (1864-1909) to describe the mathematics of packings and coverings. The term appears in the title of his Geometrie der Zahlen.
GIBBS PHENOMENON, GIBBS-WILBRAHAM CONSTANT etc. In 1898 the experimental physicist A. A. Michelson wrote to Nature, 58, (1898), 544-5 criticising the textbook account of representing discontinuous functions by Fourier series. Among the responses were two from J. W. Gibbs "Fourier Series," Nature, 59, (1898), 200 & (1899), 606. which explained the phenomena of undershoot and overshoot. M. Bôcher developed the theme and introduced the term "Gibbs's phenomenon" in his "Introduction to the Theory of Fourier's Series," Annals of Mathematics, 7, (1906), 81-152.
The Gibbs phenomenon had been discussed fifty years earlier by H. Wilbraham "On a certain periodic function," Cambridge and Dublin Mathematical Journal, 3, (1848), 198–201. Henry Wilbraham (1825–1883) published a number of mathematical papers and then made a career in the law. His contribution was first noted in 1914 by Burkhardt in his survey of the history of trigonometric series before 1850 in the Encyklopädie der mathematischen Wissenschaften 2, T.1, H.2 819-1354 (see p. 1049). (Based on E. Hewitt & R. E. Hewitt "The Gibbs-Wilbraham phenomenon: An episode in Fourier analysis," Archive for History of Exact Sciences, 21, (1979), 129-160.) See also the entries in Encyclopedia of Mathematics and MathWorld. [John Aldrich]
GÖDEL'S INCOMPLETENESS THEOREM refers to a result obtained by Kurt Gödel in his "über formal unentscheidbare Sätze der Principia Mathematica und verwandter Systeme" (On the formally undecidable theorems of Principia Mathematica and related systems),
Monatshefte für Mathematik und Physik, 38, (1931), 173-198.
The term Gödel's theorem was used by Max Black in 1933 in The Nature of Mathematics [OED].
The term Gödel's incompleteness theorem appears in W. V. Quine, "Element and Number,"
Journal of Symbolic Logic, 6, (1941), p. 140. (JSTOR search)
GOLDBACH'S CONJECTURE. The term comes from the name Christian Goldbach (1690-1764).
Théorème de Goldbach is found in G. Eneström, "Sur un théorème de Goldbach (Lettre à Boncompagni)," Bonc. Bull. (1886).
Théorème de Goldbach is found in G. Cantor, Vérification jusqu'à 1000 du théorème de Goldbach, Association Française pour l'Avancement des Sciences, Congrès de Caen (1894).
Goldbach's theorem is found in 1896 in M.-P. Stackel, "Über Goldbach's empirisches Theorem," Gött. Nachrichten, 1896.
Goldbach-Euler theorem appears in the title of an article "On the Goldbach-Euler theorem regarding prime numbers" by James Joseph Sylvester, which appeared in Nature in 1896/7.
Goldbach-Euler conjecture appears in April 1897 in an obituary of Sylvester in Johns Hopkins University Circulars: "...shortly before he died he was hopeful of being able to prove the Goldbach-Euler conjecture that every even number can be partitioned into two primes; but in this he was not successful, although he was able to narrow the issue, and to give a more precise statement of the supposed theorem."
Goldbach's problem is found in English in 1902 in Mary Winton Newson's translation of Hilbert's 1900 address in the Bulletin of the American Mathematical Society.
Goldbach's theorem occurs in English in the Century Dictionary (1889-1897).
Goldbach's hypothesis is found in J. G. van der Corput, "Sur l'hypothese de Goldbach pour presque tous les nombres pairs" Acta Arith. 2, 266-290 (1937).
Goldbach's conjecture is found in 1919 in Dickson: "No complete proof has been found for Goldbach's conjecture in 1742 that every even integer is a sum of two primes."
Goldbach's conjecture appears in the title of the novel Uncle Petros and Goldbach's Conjecture by Apostolos Doxiadis, published on March 20, 2000, by Faber and Faber.
GOLDEN SECTION. According to Greek Mathematical Works I - Thales to Euclid, "This ratio is never called the Golden Section in Greek mathematics."
Euclid used the phrase akron kai meson logon, or "extreme and mean ratio" in English. It is defined in Elements, Book VI, definition 3 (although the "extreme and mean ratio" appears implicitly already in Book II, prop. 11). [Dr. Michael N. Fried]
Leonardo da Vinci used sectio aurea (the golden section), according to H. V. Baravalle in "The geometry of the pentagon and the golden section," Mathematics Teacher, 41, 22-31 (1948).
The OED2 has: "This celebrated proportion has been known since the 4th century b.c., and occurs in Euclid (ii. 11, vi. 30). Of the several names it has received, golden section (or its equivalent in other languages) is now the usual one, but it seems not to have been used before the 19th century."
Goldenen Schnitt appears in print for the first time in 1835 in the second edition of Die reine Elementar-Mathematik by Martin Ohm:
Diese Zertheilung einer beliebigen Linie r in 2 solche Theile, nennt man wohl auch den goldenen Schnitt.In the earlier 1826 edition, the term does not occur, but instead stetige Proportion is used.
Roger Herz-Fischler in A Mathematical History of Division in Extreme and Mean Ratio (Wilfred Laurier University Press, 1987, reprinted as A Mathematical History of the Golden Number, Dover, 1998) concludes "that Ohm was not making up the name on the spot and that it had gained at least some, and perhaps a great deal of currency, by 1835" [Underwood Dudley].
The term appears in 1844 in J. Helmes in Arch. Math. und Physik IV. 15 in the heading "Eine..Auflösung der sectio aurea."
The term appears in 1849 in Der allgemeine goldene Schnitt und sein Zusammenhang mit der harmonischen Teilung by A. Wigand.
According to David Fowler, it was the publications of Adolf Zeising's Neue Lehre von den Proportionen des menschlischen Körpers (1854), Äesthetische Forschungen (1855), and Der goldne Schnitt (1884) that did the most to widely popularize the name.
Golden section is found in English in 1866 in A Dictionary of Science, Literature, and Art Vol II: "The inscription of a regular pentagon in a circle is one of the gems of Euclid's fourth book, and is made to depend upon the golden section of a line; that is to say, upon its division into two segments such that the rectangle under the smaller and the whole line is equal to the square on the greater." [Google print search by James A. Landau]
Golden mean appears in English in 1917 in On Growth and Form by Sir D'Arcy Wentworth Thompson (1860-1948): "This celebrated series, which..is closely connected with the Sectio aurea or Golden Mean, is commonly called the Fibonacci series" [OED].
Divine ratio is found in 1922 in Plane Geometry: Experiment, Classification, Discovery, Application by C. Addison Willis: "Artistic Value of Mean and Extreme Ratio.—This division of a sect possesses a remarkable artistic and psychological [page 223] interest. It has been called the 'divine ratio' or the 'golden section.'" [Google print search by James A. Landau]
The term GOODNESS OF FIT is found in the sentence, "The 'percentage error' in ordinate is, of course, only a rough test of the goodness of fit, but I have used it in default of a better." This citation is a footnote (p. 352) in Karl Pearson's "Contributions to the Mathematical Theory of Evolution. II. Skew Variation in Homogeneous Material", Philosophical Transactions of the Royal Society of London (1895) Series A, 186, 343-414. In 1900 Pearson introduced chi as a measure of goodness of fit. [James A. Landau]
See CHI SQUARE.
GOOGOL and GOOGOLPLEX are apparently found in 1937 in New Names in Mathematics by Edward Kasner. [Ivan Panchenko]
Both words are found in Edward Kasner, "New Names in Mathematics," Scripta Mathematica. 5: 5-14, January 1938 (unseen).
Googol and googolplex appear on Jan. 31, 1938, in the "Science Today" column in the Dunkirk (N. Y.) Evening Observer. The article mentions the "amusing article in Scripta Mathematica."
Googol and googolplex are found in March 1938 in The Mathematics Teacher: "The following examples are of mathematical terms coined by Prof. Kasner himself: turbine, polygenic functions, parhexagon, hyper-radical or ultra-radical, googol and googolplex. A googol is defined as 10100. A googolplex is 10googol, which is 1010100." [This quotation is part of a review of the January 1938 article above.]
Googol and googolplex were coined by the nine-year-old nephew of American mathematician Edward Kasner (1878-1955), according to Mathematics and the Imagination (1940) by Kasner and James R. Newman:
Words of wisdom are spoken by children at least as often as by scientists. The name "googol" was invented by a child (Dr. Kasner's nine-year-old nephew) who was asked to think up a name for a very big number, namely, 1 with a hundred zeros after it. He was very certain that this number was not infinite, and therefore equally certain that it had to have a name. At the same time that he suggested "googol" he gave a name for a still larger number: "Googolplex." A googolplex is much larger than a googol, but is still finite, as the inventor of the name was quick to point out. It was first suggested that a googolplex should be 1, followed by writing zeros until you got tired. This is a description of what would happen if one actually tried to write a googolplex, but different people get tired at different times and it would never do to have Carnera a better mathematician than Dr. Einstein, simply because he had more endurance. The googolplex then, is a specific number, with so many zeros after the 1 that the number of zeros is a googol. A googolplex is much bigger than a googol, much bigger than a googol times a googol. A googol times a googol would be 1 with 200 zeros, whereas a googolplex is 1 with a googol of zeros. You will get some idea of the size of this very large but finite number from the fact that there would not be enough room to write it, if you went to the farthest star, touring all the nebulae and putting down zeros every inch of the way.The Merriam Webster dictionaries identify the nine-year-old nephew as Milton Sirotta, "b. about 1929." The Social Security death index shows one person named Milton Sirotta. He was born on Mar. 8, 1911, and died in Feb. 1981, with his last residence in Mount Vernon, N. Y.
In a 2004 article in the Wall Street Journal Carl Bialik wrote:
The date for that naming is widely given on Internet encyclopedias and in recent press coverage as the late 1930s, but Dr. Kasner's living relatives say it happened closer to 1920. Milton turned nine in that year, and family archives show Dr. Kasner began referring to the number in lectures soon afterwards. ... But Denise Sirotta says her father, Edwin, told her "he was asked for a word with a sound that had a lot of O's in it" — just as googol had many zeros. Ms. Sirotta, 55 years old, adds that, according to her father, "They both came up with it. It's a sore point in my life that Milton gets the credit and my father doesn't get the credit."Ivan Panchenko provided the above quotation and writes:
This fits to the birth dates of Milton and Edwin Sirotta as given by the Social Security Death Index (March 8, 1911 and July 11, 1915, respectively; last residence of both: NY). My interpretation is that the SSDI dates are accurate (and actually belong to Kasner's nephews) while the traditional dates (about or exactly 1938 as the year of coinage, about or exactly 1929 as the year of Milton's birth) are based on the year of publication of New Names in Mathematics (1938) and the age of the nephew at the time of coinage as given in Mathematics and the Imagination (9 years; subtract 9 from 1938). The 1938 article states: "I was walking in the woods with my nephew one day, and I asked the boy to think up any name for the number, any amusing name that entered his head." It was "one day" and not necessarily in the same year. It is debatable whether it was really Milton in 1920/1921 or Edwin in 1924/1925 that Kasner was referring to. It would be clear if we knew that Kasner used the word in a lecture before 1924, but Bialik is not precise ("soon afterwards") about that matter.Merriam-Webster dictionaries pronounce googol with a secondary stress on the second syllable. Thus it is pronounced differently from the name of the Internet company Google, although that name has its origins in a misspelling of googol. See the account by David Koller.
GRAD, GRADE, GRADIAN. Grad or grade originally meant one ninetieth of a right angle, but the term is now used primarily to refer to one hundredth of a right angle.
Gradus is a Latin word equivalent to "degree."
Nicole Oresme called the difference between two successive latitudines a gradus (Smith vol. 2, page 319).
The OED2 shows a use of grade in English in about 1511, referring to one-ninetieth of a right angle.
The OED2 shows a use of grade, meaning one-hundredth of a right angle, in 1801 in Dupré Neolog. Fr. Dict. 127: "Grade .. the grade, or decimal degree of the meridian."
The term may have been used in the modern sense in the unpublished French Cadastre tables of 1801.
In 1857, Mathematical Dictionary and Cyclopedia of Mathematical Science has: "The French have proposed to divide the right angle into 100 equal parts, called grades, but the suggestion has not been extensively adopted."
In 1987 Mathographics by Robert Dixon has: "360° = 400 gradians = 2π radians."
The calculator that is part of Microsoft Windows 98, in the scientific view, allows the user to choose between degrees, radians, and (erroneously) gradients.
The Texas Instruments TI-89 Titanium calculator has three modes, radians, degrees, and gradians.
GRADIENT was introduced by Horace Lamb (1849-1934) in An Elementary Course of Infinitesimal Calculus (Cambridge: Cambridge University Press, 1897):
It is convenient to have a name for the property of a curve which is measured by the derived function. We shall use the term "gradient" in this sense. (OED)Gradient in the vector analysis sense of the vector of partial derivatives of a function of several variables did not become current until the early 20th century. It appears in H. Weber's Die partiellen differential-gleichungen der mathematischen physik nach Riemanns Vorlesungen of 1900.) The OED's earliest quotation with gradient is from J. G. Coffin's Vector Analysis (1909).
There were several earlier terms going back several decades. J. C. Maxwell originally used the term slope, e.g. in his 1873 Treatise on Electricity and Magnetism, p. 15, but in the second edition he changed this to space-variation. J. W. Gibbs favoured derivative, writing in his 1881 Elements of Vector Analysis Arranged for the Use of Students in Physics, "if u is any scalar function of position in space
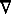u may be called the derivative of u..." This term also appears in E. B. Wilson's Vector Analysis: A Text Book for the Use of Students of Mathematics and Physics Founded upon the Lectures of J. Willard Gibbs of (1901, p. 138), although Wilson notes that the term gradient has been used as well. The gradient and the symbol grad receive more attention in Wilson's Advanced Calculus (1912, p. 172).
Sylvester used the term in a different sense in 1887 [OED].
The DSB says that Maxwell introduced the term in 1870; this seems to be incorrect.
[This entry was contributed by John Aldrich.]
GRADUATION. "The actuarial profession has for decades, indeed centuries, used age related tables, particularly (although not exclusively) of mortality, which in preparation have been subjected to the process known as graduation." These are the opening words of a 1985 review "Criteria of Smoothness" by H. A. R. Barnett, Journal of the Institute of Actuaries, 112, 331. "Graduation, or the Smoothing of Data" is the title of ch. XI of E. T. Whittaker and G. Robinson's well-known treatise of 1924, The Calculus of Observations: A Treatise on Numerical Mathematics. In it they discuss a number of "formulae of graduation" devised by actuaries for smoothing LIFE TABLES. Their oldest method is due to S. B. Woolhouse (1870) "Explanation of a New Method of adjusting Mortality Tables" Journal of the Institute of Actuaries, 15, 389. Some of the methods they describe amount to the application of the METHOD OF LEAST SQUARES.
See SMOOTHING.
GRAHAM'S NUMBER is named for Ronald Graham.
The term "Graham-Spencer number" appears in N. D. Nenov and N. G. Khadzhiivanov, "On the Graham-Spencer number," C. R. Acad. Bulg. Sci. 32 (1979).
The term "Graham's number" appears the 1985 Guinness Book of World Records, and it may appear in earlier editions of that book.
The number is discussed in M. Gardner, "Mathematical Games," Sci. Amer. 237, Nov. 1977.
GRAM-SCHMIDT ORTHOGONALIZATION. When Erhard Schmidt presented the formulae on p. 442 of his "Zur Theorie der linearen und nichtlinearen Integralgleichungen. I. Teil: Entwicklung willkürlicher Funktionen nach Systemen vorgeschriebener," Math. Ann., 63 (1907), 433-476 he said that essentially the same formulae were in J. P. Gram's "Ueber die Entwickelung reeler Funtionen in Reihen mittelst der Methode der kleinsten Quadrate," Jrnl. für die reine und angewandte Math. (1883), 94, 71-73. Modern writers, however, distinguish the two procedures, sometimes using the term "Gram-Schmidt" for the Schmidt form and "modified Gram-Schmidt" for the Gram version. R. W. Farebrother Linear Least Squares Computations (1988) gives this information and proposes that the Gram form be re-named "Laplace's method" as it was already given in the First Supplement (1816) of Laplace's Théorie Analytique des Probabilités, p. 497ff.
A JSTOR search found "Gram-Schmidt's orthogonalization process" in Y. K. Wong "An Application of Orthogonalization Process to the Theory of Least Squares," Annals of Mathematical Statistics, 6, (1935), 53-75.
GRAPH (of a function). The phrase graph of a function was used by Chrystal in 1886 in Algebra I. 307: "This curve we may call the graph of the function" [OED].
GRAPH (verb) is found in 1898 in Perry, Applied Mechanics 21: "Students will do well to graph on squared paper some curves like the following" [OED].
GRAPH and GRAPH THEORY. On April 27, 1961, the Humboldt Standard has: "For the Friday assembly, at 10 a.m. at Sequoia Theater, the professor will discuss 'The Graph Theory as a Model in the Social Sciences.'"
On June 5, 1963, the Appleton Post-Crescent has: "The potential uses of graph theory in anthropology include subjects such as kinship and descent, social structure and organization, geographical proximity and communication, economic reciprocity and others."
Graph Theory 1736-1936 (1976) by N. L. Biggs, E. K. Lloyd and R. J. Wilson begins with Euler's KÖNIGSBERG BRIDGE PROBLEM and ends with König's graph theory of 1936. Among the contributors in between was Hamilton; for the terms associated with him see HAMILTON.
Regarding the term graph, Biggs, Lloyd and Wilson (p. 65) write that James Joseph Sylvester "conceived the notion that there is a relationship between chemistry and algebra, exemplified by the use of graphic notation. He published a note on his ideas in February 1878, in the scientific journal Nature. In this note the word 'graph' is used in our sense for the first time; it is clearly derived from the chemical graphic notation'."
In that note "Chemistry and Algebra", Sylvester wrote: "Every invariant and covariant thus becomes expressible by a graph precisely identical with a Kekulean diagram or chemicograph" Coll. Math. Papers III pp. 103-4.
Martin Gardner wrote in Scientific American in April 1964, "In the 1930s, the German [sic] mathematician Dénes König made the first systematic study of all such patterns, giving them the generic name 'graphs.'" [König was actually Hungarian.]
D. König (1884-1944) published Theorie der endlichen und unendlichen Graphen in Leipzig in 1936. Biggs, Lloyd and Wilson (p. 206) reflect, "The year 1936 marked the two-hundredth anniversary of Euler's article on the problem of the Königsberg bridges, and so it was a fitting coincidence that the first book on graph theory should be published in that year."
Graph theory appears in English in W. T. Tutte, "A ring in graph theory," Proc. Camb. Philos. Soc. 43, 26-40 (1947).
Len Smiley, Adalbert Kerber, and John Aldrich contributed to this entry.
GREAT CIRCLE is found in English in 1594 in the title, The Sea-mans Secrets .. wherein is taught the 3 kindes of Sailing, Horizontall, Paradoxall, and Sayling vpon a great Circle, by John Davis. Davis wrote, "Navigation consiseth of three parts, ... The third is a great Circle Navigation, which teacheth bow upon a great Circle, drawn between any two places assigned (being the only shortest way between place and place) the Ship may be conducted and to performed by the skilful application of Horizontal and Paraboral Navigation."
GREATEST COMMON DIVISOR in Latin books was usually written as maximus communis divisor.
Cataneo in 1546 used il maggior commune ripiego in Italian.
Greatest common measure is found in English in 1570 in Billingsley, Elem. Geom.: "It is required of these three magnitudes to finde out the greatest common measure" [OED].
Cataldi in 1606 wrote massima comune misura in Italian.
Greatest common divisor is found in English in 1694 in Pleasure with Profit: Consisting of Recreations of Divers Kinds by William Leybourn: "If possible, reduce the two Fractions propos'd into the least Term, by the greatest Common Divisor, (per Lemma II.) Then multiply alternately as before." [Google print search by James A. Landau]
Highest common divisor is found in 1830 in A Treatise on Algebra by George Peacock. [Google print search]
Greatest common factor is found in 1835 in Library of Useful Knowledge: Mathematics. II. [Google print search by James A. Landau]
Highest common factor is found in 1843 in The Penny Cyclopædia of the Society for the Diffusion of Useful Knowledge.
[Google print search]
Olaus Henrici (1840-1918), in a Presidential address to the London Mathematical Society in 1883, said, "Then there are processes, like the finding of the G. C. M., which most boys never have any opportunity of using, except perhaps in the examination room."
GREEN'S FUNCTION. Greensche Function appears in 1861 in a paper by Carl Neumann in Crelle's Journal 59, 335.
The term Green's function is also used in statistical physics. In this sense the term was probably first used in 1850 by the Rev. Samuel Haughton in a note "On the function peculiar to a System of attracting and repelling Molecules" in the Proceedings of the Royal Irish Academy. [Jan Peter Schäfermeyer]
GREEN'S THEOREM was so named by William Thomson (Lord Kelvin). In his "On Peristaltic Induction of Electric Currents," Proceedings of the Royal Society, 8, (1856 - 1857), p. 124 Thomson relates how he found the result and published it before learning that it was in George Green's (1793-1841) Essay on the Mathematical Theory of Electricity and Magnetism (1828) ( Green's Papers, pp. 1-115). Thomson arranged for the re-publication of Green's privately published Essay and brought Green to the attention of other scientists. "Green's theorem" was given a vector treatment by P. G. Tait in "On Green's and other allied theorems,"Trans. of Edinb. (1870) Scientific Papers I, pp. 136-50.
The theorem bears the name of Mikhail Ostrogradski in Russia.
GREGORY'S SERIES is the name mathematicians writing in English generally use for the Maclaurin series for arc tan. The series was obtained by James Gregory in 1671 but the series—especially the case x = 1 when the series is for — is also associated with Leibniz, who obtained it in 1674. However the result had been obtained around three hundred years earlier by the Indian mathematician Madhava. Western mathematicians only learnt of Madhava's contribution in the twentieth century. For details see Katz section 12.3 "Power Series."
The term Gregory's series is well entrenched in the English literature. Mr. Gregory's series appears in 1714 in the famous adjudication of the priority claims of Newton and Leibniz regarding the invention of the calculus, "An Account of the Book entitled Commercium Epistolicum Collinsii et aliorum, De Analysi promota; Published by order of the Royal-Society, in relation to the Dispute between Mr. Leibnitz and Dr. Keill, about the Right of Invention of the Method of Fluxions, by some call'd the Differential Method" Philosophical Transactions 1714, pp. 173-224. This unsigned document was written by Newton himself.
The term Leibniz series has always been more common in Continental Europe. The combinations Gregory-Leibniz and Leibniz-Gregory are also used. The use of Madhava seems to be confined to historical works such as R. C. Gupta, "The Madhava-Gregory series," Math. Education 7 (1973), B67-B70.
James A. Landau contributed to this article. See SERIES.
GREGORY-NEWTON INTERPOLATION FORMULA. The formula was first given in 1670 by James Gregory but Gregory did not publish it. Isaac Newton, working independently, published it in 1687 in his Principia. In 1924 E. T. Whittaker and G. Robinson wrote in their Calculus of Observations (p. 12), "The formula (1) is often referred to as Newton's formula of interpolation, although it was discovered by James Gregory in 1670." They referred instead to the "Gregory-Newton formula" and their practice has been widely followed.
(See Erik Meijering A Chronology of Interpolation: From Ancient Astronomy to Modern Signal and Image Processing Proceedings of the IEEE, 90, (2002), p. 322.)
See INTERPOLATION.
GRELLING-NELSON PARADOX. See the AUTOLOGICAL and HETEROLOGICAL.
GROEBNER BASES. Bruno Buchberger introduced Groebner bases in 1965 and named them for W. Gröbner (1899-1980), his thesis adviser, according to Ideals, Varieties, and Algorithms by Cox, Little, and O'Shea [Paul Pollack]. See the entry in Encyclopedia of Mathematics.
GROUP and GROUP THEORY. Evariste Galois introduced the term group in the form of the expression groupe de l'équation in his "Mémoire sur les conditions de résolubilité des équations par radicaux" (written in 1830 but first published in 1846) Oeuvres mathématiques. p. 417. Cajori (vol. 2, page 83) points out that the modern definition of a group is somewhat different from that of Galois, for whom the term denoted a subgroup of the group of permutations of the roots of a given polynomial.
Group appears in English in Arthur Cayley, "On the theory of groups, as depending on the symbolic equation θn = 1," Philosophical Magazine, 1854, vol. 7, pp. 40-47, Reprinted in Collected Works II, pp. 123-130: "A set of symbols, 1, α, β, ..., all of them different, and such that the product of any two of them (no matter what order), or the product of any one of them into itself, belongs to the set, is said to be a group." The paper also introduced the term theory of groups. At the time this more abstract notion of a group made little impact.
Klein and Lie use the term "closed system" in their "Über diejenigen ebenen Curven, welche durch ein geschlossenes System von einfach unendlich vielen vertauschbaren linearen Transformationen in sich übergehen," Mathematische Annalen, 4, (1871), 50-84. Klein adopted the term gruppe in his " Vergleichende Betrachtungen über neuere geometrische Forschungen" written in 1872 and reissued in Mathematische Annalen, 43, (1893),63-100. See the entry ERLANGEN PROGRAM.
Group-theory is found in English in 1888 in George Gavin Morrice's translation of Felix Klein, Lectures on the Ikosahedron and the solution of Equations of the Fifth Degree. [Google print search]
See MacTutor Hilbert-Weyl discussion between 1919 and 1922, occurring e.g. in Weyl's "Über die neue Grundlagenkrise der Mathematik", Math.Z. 10 (1921) 39-79."
The term GUDERMANNIAN was introduced by Arthur Cayley (1821-1895), according to Chrystal in Algebra, vol. II. The term appears in an 1862 article by Cayley in the Philosophical Magazine [Collected Mathematical Papers vol. 5 p. 86]. The term is named for Christoph Gudermann. See MathWorld.
GYROID, as the name of a minimal surface, was coined by Alan H. Schoen. (The discovery of this intriguing surface is also due to him: "Infinite Periodic Minimal Surfaces Without Selfintersections." NASA Tech. Note No. D-5541. Washington, DC, 1970.)
On October 31, 2000 Schoen wrote (private correspondence):
My records don't show exactly when I thought of the name "gyroid", but I do find in my files a copy of a letter to Bob Osserman on March 3, 1969 in which I wrote as follows:Gyroid (in crystallography) is found in English in 1872 in Diagrams to Illustrate the Lectures on Crystallography by T. Egleston. [Google print search by James A. Landau]
The gyroid. This is my latest choice of a name for this surface, which is the only surface associate to the two intersection-free adjoint Schwarz surfaces ("P" and "D") that is free of self-intersections. (Webster's 3d International Dictionary defines gyroidal as "spiral or gyratory in arrangement -- used esp. of the planes of crystals".)
When Bob wrote back shortly afterward, he mentioned that he approved of the name. I suppose it was at least in part my having studied Latin and Greek in highschool and college that impelled me to search for a classical-sounding name for this surface. As soon as I stumbled on a name that shared its 'oid' ending with the helicoid and catenoid, I decided to look no further!
This entry was contributed by Carlos César de Araújo. See MathWorld.