Earliest Known Uses of Some of the Words of Mathematics (H)
HAAR MEASURE. Alfréd Haar described the an invariant measure on locally compact groups in his "Der Massbegriff in der Theorie der kontinuierlichen Gruppen" Annals of Mathematcs, 34, (1933), 147–169. The expression Haar measure was soon in circulation: a JSTOR search found it in S. Bochner's "Average Distribution of Arbitrary Masses under Group Translations," Proceedings of the National Academy of Sciences, 20, (1934), 206-210. See also Enyclopedia of Mathematics.
HADAMARD or SCHUR PRODUCT of matrices. There is nothing puzzling about the association of Schur with the entry-wise product for he wrote the seminal paper on the subject: Bemerkungen zur Theorie der beschränkten Bilinearformen mit unendlich vielen Veränderlichen, Journal für die reine und angewandte Mathematik, 141, (1911), 1-28.
Hadamard, on the other hand, never wrote about this type of product.
In 1941, Elementary Theory of Matrices by Paul Richard Halmos (as digitized by Google) shows the term Hadamard product in the table of contents, giving page number 48. However the term does not appear anywhere else in the book, and page 48 has: "As a consequence of the preceding section it is very easy to prove a remarkable theorem on non-negative matrices, due to L. Schur."
The popularity of the expression Hadamard product appears to derive from its appearance in Halmos's Finite-Dimensional Vector Spaces (1948). Halmos later explained that von Neumann used the expression in lectures and it has been suggested that von Neumann was alluding to Hadamard's well-known work on products of power series ("Théorème sur les séries entières," Acta Mathematica, 22, (1899), 55-63) and that von Neumann was associating Hadamard's name with term-by-term products of all kinds. (Based on the historical remarks in R. A. Horn's chapter "The Hadamard Product" in C. R. Johnson (ed.) Matrix Theory and Applications, AMS (1990).) [This entry was contributed by John Aldrich. James A. Landau found the 1941 reference.]
HAHN-BANACH THEOREM in functional analysis. The result is due to Hans Hahn "Ueber lineare Gleichungsysteme in linearen Räume," J. Reine Angew. Math., 157, (1927), 214–229 and Stefan Banach "Sur les fonctionelles linéaires," Studia Math., 1, (1929), 211–216 and "Sur les fonctionelles linéaires II," Studia Math., 1 (1929), 223–239. See also Enyclopedia of Mathematics.
Hahn-Banach theorem is found in English in L. Nachbin, On the Hahn-Banach theorem, Amis Acad. Brasil. Ci., 21, (1949), 151-154. [Google print search by James A. Landau]
HAIRY BALL THEOREM. James A. Landau recalls that in Freshman Orientation at Michigan State in 1965, a math professor gave a talk about topology. The professor said, "I know it's hard to believe [it was very windy that day] but there is a point on the earth at which the wind does not blow." Landau also recalls that the professor then went on to say this theorem meant "you can't comb a hairy billiard ball without leaving a cowlick."
According to M. W. Hirsch Differential Topology (1976) Every vector field on S2n is zero somewhere; more picturesquely a hairy ball cannot be combed." (p.125) Hirsch refers to this result as the "so-called 'hairy ball theorem'" and the name appears to have become popular in the 1970s. However the theorem goes back to L. E. J. Brouwer "Über Abbildung von Mannigfaltigkeiten," Mathematisches Annalen, (1912), 97-115 and beyond that to Ch XIII pp. 203-8 of Poincaré's "Sur les courbes définies par les équations différentielles," Journal de mathématiques pures et appliquées (1885), 167-244.
HALMOS. See the entry on Earliest Uses of Symbols of Set Theory and Logic.
HAM SANDWICH THEOREM. Hugo Steinhaus posed the following problem in the famous Lvov Scottish Book "Given are three sets A1, A2, A3 located in the 3-dimensional Euclidean space and with finite Lebesgue measure. Does there exist a plane cutting each of the three sets A1, A2, A3 into two parts of equal measure? The same for n sets in the n-dimensional space." A solution was published in a note, "A Note on the Ham Sandwich Theorem," in the journal Mathesis Polska in 1938. The note was by Steinhaus and others but the proof they presented was due to Banach; this is based on the Borsuk-Ulam Theorem. The note indicates that the problem can be formulated as follows: "Can we place a piece of ham under a meat cutter so that meat, bone and fat are cut in halves?" (Based on WA Beyer, A Zardecki "The early history of the ham sandwich theorem," American Mathematical Monthly, January 2004, pp. 58-61, which contains a translation of the original note.)
See the entry BORSUK-ULAM THEOREM
HAMILTON and HAMILTONIAN are used to recall the work of William Rowan Hamilton (1805-1865). The terms in use today derive from his reformulation of mechanics and from the "Icosian game" which he invented and marketed. The game is now understood in terms of graph theory; see Mathworld. Hamilton's long years of work on QUATERNIONS are recalled only in the name CAYLEY-HAMILTON THEOREM.
Hamilton's two essays on a General Method in Dynamics in the Philosophical Transactions of the Royal Society of London (1834-5) gave rise to Hamilton's principle, the Hamiltonian form of the equations of motion and the Hamiltonian function. All these terms appear in E. T. Whittaker Treatise on the Analytical Dynamics of Particles and Rigid Bodies (1904). The OED has a quotation from 1858, A. Cayley writing about forms of the equations of motion in Rep. Brit. Assoc. Adv. Sci. 1857 I. 15: "When there is no force function..the forms corresponding to the untransformed forms in and are as follows, viz. the Lagrangian form is dq/dt = q´, d(dT/dq´)/dt - dT/dq = , and the Hamiltonian form is dq/dt = dT/dp, dp/dt = - dT/dq + ."
Hamiltonian mechanics involved the calculus of variations and so Hamiltonian terms appear in that field as well. A relatively recent example is the use of the letter H (for Hamiltonian) in The Mathematical Theory of Optimal Processes (1961) by L. S. Pontryagin, V. G. Boltyanskii, R. V. Gamrelidze & E. F. Mishchenko.
Hamiltonian Game is found in 1892 in the second edition of Mathematical Recreations and Essays by W. W. Rouse Ball. [Google print search by James A. Landau]
Hamiltonian circuit is found in W. T. Tutte, "On Hamiltonian circuits," J. London Math. Soc. 21, 98-101 (1946).
Hamiltonian path is found in V. Mierlea, "An algorithm for finding the minimal length Hamiltonian path in a graph," Econom. Comput. econom. Cybernetics Studies Res. 1973, No. 2, 77-89 (1973).
HANDWAVING. This slang term first appears in print in the 1960s. A JSTOR search found these early examples: "By keeping the handwaving and the use of the villainous "it is clear that" to a minimum, the author has imposed discipline on and revealed the beauty of a subject that has attracted hitherto the more than its share of mathematical cavaliers" from Wimp SIAM Review, 7, (1965), p. 577 and "The presentation is ... for the most parts rigorous. Unfortunately there is a great deal of handwaving in the geometric parts of the chapter on conformal mapping…" from Leibowitz in American Mathematical Monthly, 74, (1967), p. 1154.
HARD and SOFT MATHEMATICS. "In mathematical slang, formal, abstract theorems are referred to as 'soft' and concrete theorems are called 'hard.' The words 'hard' and 'soft' are not to be taken in general as indications of difficulty or lack thereof; 'hard' analysis is not necessarily more (or less) difficult than any other kind of mathematics..." T. W. Gamelin & R. E. Greene Introduction to Topology, (1983, p. 74.)
These terms have been around for a long time but notoriously the history of slang is hard to document. In 1964 Jean Dieudonné was complaining of "traditional jokes" about hard and soft mathematics becoming "a little stale." ("Recent Developments in Mathematics," American Mathematical Monthly, 71, p. 247). JSTOR
It seems likely that the terms originated as extensions of the older terms hard analysis and soft analysis. JSTOR sightings of these terms date only from the late 1950s although it is clear that the terms were already well-established. Typical subjects for hard analysis included the SPECIAL FUNCTIONS, while soft analysis was often another term for FUNCTIONAL ANALYSIS.
HARDY CLASSES and SPACES. According to the Encyclopedia of Mathematics article on Hardy Classes F. Riesz introduced the Hardy class of function in his "Über die Randwerte einer analytischen Funktion" Math. Z., 18 (1923) pp. 87-95. The name was chosen in honour of G. H. Hardy. The higher dimensional analogues called Hardy spaces were introduced by E. Stein and G. Weiss, "On the theory of harmonic functions of several variables" Acta Math. , 103 (1960) pp. 25-62.
HARDY-LITTLEWOOD THEOREM. The 35-year collaboration between G. H. Hardy and J. E. Littlewood produced numerous theorems. The Hardy-Littlewood Tauberian theorem was given in G.H. Hardy and J.E. Littlewood, "Tauberian theorems concerning power series and Dirichlet's series whose coefficients are positive," Proc. London. Math. Soc. (2), 13, (1914) pp. 174-191. The Hardy-Littlewood maximal theorem was given in "A maximal theorem with function-theoretic applications," Acta Math., 54 (1930) pp. 81-116.
Hardy-Littlewood Theorem is found in 1923 in Proceedings of the Cambridge Philosophical Society: Mathematical and plysical sciences, Volume 21: "the factor ζ(s + r) by means of an important equation recently discovered by Hardy and Littlewood and named by them the Approximate Functional Equation for the ζ-function. The Hardy-Littlewood Theorem gives the following representation for the ζ-function in the critical strip . . ." [Google print search by James A. Landau]
See TAUBERIAN THEOREMS.
The HARDY-RAMANUJAN THEOREM was given by G. H. Hardy and S. Ramanujan "The normal number of prime factors of a number n, "Quart. J. Math. , 48, (1917) pp. 76-92. See the Encyclopedia of Mathematics article on the Hardy-Ramanujan theorem.
HARMONIC ANALYSIS. According to Grattan-Guinness (679), the phrase is due to W. Thomson (later Lord Kelvin). In an obituary of Archibald Smith (Proc. Royal Soc. 22. (1873 - 1874) p. vi) Thomson wrote "One of Smith's earliest contributions to the compass problem was the application of Fourier's grand and fertile theory of the expansion of a periodic function in series of sines and cosines of the argument and its multiples, now commonly called the harmonic analysis of a periodic function." Thomson invented the harmonic analyser; in 1879 the Royal Society allocated him £50 for "completing a Tidal Harmonic Analyser" (Proc. Royal Soc., 29, 442.)
A Google print search finds the term harmonic analysis in a note added in Dec. 1863 to "Dynamical Problems regarding Elastic spheroidal Shells and Spheroids of Incompressible Liquid," by Professor W. Thomson LL.D., read Nov. 27, 1862. [James A. Landau]
In statistics harmonic analysis is found in R. A. Fisher, " Tests of Significance in Harmonic Analysis.," Proc. Roy. Soc. A, 125, 54-59 (1929) [John Aldrich].
HARMONIC ANALYZER. A Google print search finds this term in the Proceedings of the Royal Society of London in the title of the paper "Harmonic Analyzer," Shown and explained by Sir William Thomson, F.R.S., Professor of Natural Philosophy in the University of Glasgow. Received May 9, 1878. [James A. Landau]
HARMONIC FUNCTION. According to Kline (p. 685) William Thomson (later called Lord Kelvin) introduced the term in 1850. The OED's earliest quotation is for spherical harmonic function as used in Thomson & P. G. Tait's Treatise on Natural Philosophy (1867, I. i. App. B): "The .. method .. commonly referred to by English writers as that of 'Laplace's Co-efficients'..is here called spherical harmonic analysis.. A spherical harmonic function is defined as a homogeneous function, V, of x, y, z, which satisfies the equation
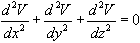 ." In a post to the Historia Matematica mailing list Emili Bifet gives an earlier reference: Thomson's "Dynamical Problems regarding Elastic Spheroidal Shells and Spheroids of Incompressible Liquid," Philosophical Transactions of the Royal Society, 153 (1863), p. 585.
." In a post to the Historia Matematica mailing list Emili Bifet gives an earlier reference: Thomson's "Dynamical Problems regarding Elastic Spheroidal Shells and Spheroids of Incompressible Liquid," Philosophical Transactions of the Royal Society, 153 (1863), p. 585.
HARMONIC MEAN, HARMONIC PROPORTION. A surviving fragment of the work of Archytas of Tarentum (ca. 350 BC) states, "There are three means in music: one is the arithmetic, the second is the geometric, and the third is the subcontrary, which they call harmonic."
The term harmonic mean was also used by Aristotle.
According to one theory, the term subcontrary may refer to the fact that a tone based on this mean reverses the order of the two fundamental musical intervals in a scale.
The term harmonic may have been used because it produced a division of the octave in which the middle tone stood in the most harmonious relationship to the tonic and the octave.
In a message posted to a history of mathematics mailing list in 2003, Michael N. Fried writes:
In the Introduction to Arithmetic (Arithmetike eisagoge), Nicomachus gives his account of the name harmonic proportion (which defines the harmonic mean) in contradistinction to the arithmetic and geometric proportions (which define the arithmetic and geometric means, respectively). He writes as follows:Harmonical proportion appears in English in 1660 in R. Coke, Justice Vind., Arts & Sc.: "Harmonical proportion increases neither equally nor proportionally: nor do the extremes added or multiplied produce the like number with the mean" [OED].The harmonic proportion was so called because the arithmetic proportion was distinguished by quantity, showing an equality in this respect with the intervals from one term to another [for if m is the mean between a and b, then a-m is precisely the same as m-b], and the geometric by quality, giving similar qualitative relations between one term and another [for a-m:m-b is precisely the same ration as a:m and m:b], but this form, with reference to relativity, appears now in one form, now in another, nether in its terms exclusively nor in its differences exclusively, but partly in the terms and partly in the differences [here, a-m:m-b is the same ratio only as a:b]; for as the greatest term is to the smallest, so also is the difference between the greatest and the next greatest, or middle, term to the difference between the least term and the middle term, and vice versa" (II.25, trans. by Martin Luther D'Ooge)I am not quoting this passage to contradict the musical explanations for the word "harmonic" that have been already given over the past few days. Indeed, immediately following this passage Nicomachus reminds us of the connection between the relative, the harmonic, and the musical. But it is important to remember that both music and harmony had, for Nicomachus, among others in antiquity, a wider intention than merely aural phenomena--and here is where one must tread with care.
Harmozein just means to join or to fit together--for example, in Elem. IV.1, when Euclid requires a segment of a given length to be fit in a given circle, he uses the related word, enarmozein. Consonance is a fitting together of sounds and is just an example of a more general fitting together of different parts of the world. It is in this spirit that earlier in the Introduction Nicomachus gives own definition, if you like, of the word harmonic:Everything that is harmoniously constituted is knit together out of opposites and, of course, out of real things; for neither can non-existent things be set in harmony, nor can things that exist, but are like one another, nor yet things that are different, but have no relation one to another. It remains, accordingly, that those things out of which a harmony is made are both real, different, and things with some relation to one another" (I.6, trans. again by M. L. D'Ooge)Incidentally, Archytas, for one, refers not only to the harmonic mean as musical, but equally so to the geometric and arithmetic means!
According to the Catholic Encyclopedia, the word harmonic first appears in a work on conics by Philippe de la Hire (1640-1718) published in 1685.
Harmonical mean is found in English in Philosophical Transactions For the Months of May and June, 1704: "Afterwards there are several Problems concerning Arithmetical, Geometrical, and Harmonical mean proportional betwixt two Extreams, and divers Methods for describing the Conick sections by points." [Google print search by James A. Landau]
Harmonic mean is found in 1821 in Geometrical Problems deducible from the first six books of Euclid by Miles Bland. [Google print search by James A. Landau]
HARMONIC NUMBER. A treatise on trigonometry by Levi ben Gerson (1288-1344) was translated into Latin under the title De numeris harmonicis.
HARMONIC PROGRESSION. Sir Isaac Newton used the phrase "harmonical progression" in a letter of 1671 (New Style) [James A. Landau].
In a letter dated Feb. 15, 1671, James Gregory wrote to Collins, "As to yours, dated 24 Dec., I can hardly beleev, till I see it, that there is any general, compendious & geometrical method for adding an harmonical progression...."
The term HARMONIC RANGE developed from the Greek "harmonic mean." Collinear points form a harmonic range when the length is the harmonic mean of and , i.e. . It's then easy to deduce the more modern condition that the cross ratio .
In "A Treatise of Algebra," 1748, Appendix, p. 20, Maclaurin says "atque hae quatuor rectae, Cl. D. De la Hire, Harmonicales dicuntur." In "Nouvelle methode en geometrie pour les sections des superficies coniques et cylindriques ...," 1673, by Philippe de la Hire, p.1, his first words are: "Definition. J'appelle une ligne droitte AD couppée en 3 parties harmoniquement quand le rectangle contenu sous la toutte & la partie du milieu est égal au rectangle contenu sous les deux parties extremes ...." This statement is another variant of the conditions given above, disregarding signs. [Ken Pledger]
Harmonic range is found in English in 1857 in The Quarterly Journal of Pure and Applied Mathematics. [Google print search by James A. Landau]
HARMONIC SERIES appears in 1727-51 in Chambers Cyclopedia: "Harmonical series is a series of many numbers in continual harmonical proportion" [OED].
The term HARMONIC TRIANGLE was coined by Leibniz (Julio González Cabillón).
HAT MATRIX in least squares analysis. The term appears in the title of David C. Hoaglin and Roy E. Welsch's "The Hat Matrix in Regression and ANOVA," American Statistician, 32, (1978), 17-22. They write, "The term "hat matrix" is due to John W. Tukey who introduced us to the technique about ten years ago."
David (1998)
The HAUPTSATZ. In German this label for "main theorem" is attached to several propositions --see Wikipedia–but in English mathematics/mathematical logic it is now attached to only one of these, der Gentzensche Hauptsatz. The proposition appears in Gerhard Gentzen's "Untersuchungen über das logische Schließen," Mathematische Zeitschrift, 39, (1934-5), 405-431. In English "Gentzen's Hauptsatz" is mentioned in the Journal of Symbolic Logic of 1938 and for decades it was referred to by this name or as "the Gentzen Hauptsatz." Eventually it became possible to drop the reference to Gentzen without risk of confusion, as in the title of D. Prawitz's "Hauptsatz for Higher Order Logic," Journal of Symbolic Logic, 33, (1968), 452-457. In English the theorem is also called the "cut-elimination theorem"; see Wikipedia. [John Aldrich]
The HAUPTVERMUTUNG refers to a conjecture originally formulated by Steinitz and Tietze in 1908. In their Topologie Alexandroff aand Hopf (1935) call it "die sog. Hauptvermutung der kombinatorischen Topologie" (the so-called main conjecture of combinatorial topology. In English the short form "Hauptvermutung" appears in quotes in J. H. C. Whitehead's "On the Homotopy Type of Manifolds," Annals of Mathematics, (1940) but from around 1950 the word has appeared without quotes. Thus a description in German of general application has become the English name for a particular conjecture. See Wikipedia and the Edinburgh Hauptvermutung page which makes available many of the main contributions. [John Aldrich]
HAUSDORFF MEASURE occurs in E. Best, "A theorem on Hausdorff measure," Quart. J. Math., Oxford Ser. 11, 243-248 (1940).
HAUSDORFF PARADOX refers to a result in Felix Hausdorff's (1868-1942) "Bemerkung über den Inhalt von Punktmengen," Mathematische Annalen, 75, (1914), 428-433: that one half of a sphere is congruent to one third of the same sphere. According to Gregory Moore Zermelo's Axiom of Choice: Its Origins, Development and Influence (1982, pp. 185-8) Hausdorff was demonstrating the non-existence of a certain kind of measure: if the measure existed the congruence proposition would follow. Émile Borel was the first to call the result a paradox: "The contradiction has its origins in the application of ... Zermelo's Axiom of Choice.... The paradox results from the fact that A is not defined, in the logical and precise sense of the word defined. If one scorns precision and logic one arrives at contradictions." (Moore's translation from Borel's Leçons sur la théorie des functions (2nd edition 1914))
See AXIOM OF CHOICE, BANACH-TARSKI PARADOX and PARADOX
HAUSDORFF SPACE is found in E. W. Chittenden, "On the Metrization problem and Related Problems in the Theory of Abstract Sets," Bull. Amer. Math. Soc. (1927) 33, pp. 13-34. Referring to Hausdorff's Grundzüge der Mengenlehre, Chittenden writes, "3. Hausdorff Spaces. A remarkable and important class of topological spaces has been defined by F. Hausdorff ... ." (p. 15)
The term HAVERSINE was introduced by James Inman (1776-1859) in 1835 in the third edition of Navigation and Nautical Astronomy for the use of British Seamen.
HAZARD RATE came into use in statistics in the 1960s as a general term for what is called the force of mortality in demography and the intensity function in extreme value theory. David (2001) finds "hazard rate" in R. E. Barlow; A. W. Marshall & F. Proschan "Properties of Probability Distributions with Monotone Hazard Rate," Annals of Mathematical Statistics, 34, (1963), 375-389. A JSTOR search found "death-hazard rate" in D. J. Davis "An Analysis of Some Failure Data," Journal of the American Statistical Association, 47, (1952), 113-150.
HEINE-BOREL THEOREM. Heine's name was connected to this theorem by Arthur Schoenflies in 1900, although he later omitted Heine's name. The validity of the name has been challenged in that the covering property had not been formulated and proved before Borel. (DSB, article: "Heine")
A Google print search shows Heine-Borel'schen Theorems in "Bericht uber die Mengenlehre" by Arthur Schoenflies in Jahresbericht der Deutschen Mathematiker-Vereinigung, (1899). [James A. Landau]
Grattan-Guinness (1997, pp. 671-2) refers to Borel's doctoral thesis of 1894 (his 23rd year), published in Ann. de l'école Normale, 12, (1895), 9-55. Borel "threw off a remark which was later recognized as an important pioneering example of a covering theorem: if every point on a line can be covered by a denumerable number of subintervals, then in fact a finite number could do the job .... [The covering technique of Heine in 1872] is the trivial one of dividing the interval into a finite number of subintervals."
In June 1907 in the Bulletin des Sciences mathématiques, Lebesgue denied any paternity of the theorem and wrote that in his opinion the name of the theorem should bear only the name of Borel [Udai Venedem].
The term HELIX is due to Archimedes, "to a spiral already studied by his friend Conon" (Smith vol. 2, page 329). It is now known as the spiral of Archimedes.
The HELMERT TRANSFORMATION is an orthogonal transformation that the geodesist F. R. Helmert used to obtain the distribution (in effect) of the sample variance for a normal population. Helmert used it in his paper on the accuracy of PETERS' METHOD, "Die Genauigkeit der Formel von Peters zur Berechnung des wahrscheinlichen Fehlers directer Beobachtungen gleicher Genauigkeit," Astronomische Nachrichten, 88, (1876), 192-218. An extract from the paper is translated and annotated in H. A. David & A. W. F. Edwards (eds.) Annotated Readings in the History of Statistics (2001). Helmert was a well-known writer on the theory of errors and his work was described in German textbooks. However, Student (1908) and Fisher (1920) did not know it and re-derived the distribution. In 1931 Karl Pearson drew attention to Helmert in a "Historical Note on the Distribution of the Standard Deviations of Samples of any Size Drawn from an Indefinitely Large Normal Parent Population," Biometrika, 23, 416-418. Pearson's suggestion that the distribution be named after Helmert was not taken up but references to Helmert's transformation followed, e.g. in R. C. Geary's (1936), "The Distribution of 'Student's' Ratio for Non-Normal Samples," Supplement to the Journal of the Royal Statistical Society, 3, 178-184.
This entry was contributed by John Aldrich, based on David & Edwards. There is also a discussion in Hald (1998). See also CHI SQUARE.
The term HEMIHEDRON was coined by Cayley according to Arthur Cayley: Mathematician Laureate of the Victorian Age by Tony Crilly.
HEPTAGON. In 1551 in Pathway to Knowledge Robert Recorde used septangle.
Heptagon appears in English in 1570 in Sir Henry Billingsley's translation of Euclid's Elements.
HEPTAKAIDECAGON (17-sided polygon) appears in Webster's Third New International Dictionary (1961).
HERMITE POLYNOMIAL (also known as Hermite-Chebyshev polynomial) is named after Charles Hermite who gave the construction in his "Sur un nouveau développement en série de functions," Compt. Rend. Acad. Sci. Paris, 58, (1864), 93-100 and 266-273, reprinted in Oeuvres. 2, pp. 293-308. The construction had been described a few years earlier by P. L. Chebyshev, "Sur le développement des fonctions à une seule variable," Bull. ph.-math., Acad. Imp. Sc. St. Pétersbourg 1, (1859), 193-200, reprinted in Oeuvres, 1, pp. 501-508. Hald (1998, p. 341) reports that Laplace had used polynomials proportional to Hermite's in his analysis of a diffusion problem in 1811.
Regarding the use of these polynomials in English language statistics, they appear to have become prominent in the 1920s. A JSTOR search found "Hermite's polynomial" in Alf. Guldberg "Expansions useful in the theory of frequency distributions," Journal of the Royal Statistical Society, 83, (1920), 127-130. In his Advanced Theory of Statistics, I of 1943 M. G. Kendall noted Chebyshev's priority and accordingly used the term "Tchebycheff-Hermite polynomial," However this ordering is rare and even "Hermite-Chebyshev" is much less common than just "Hermite."
Hermite polynomial is found in 1939 in Orthogonal Polynomials by Gabor Szegö [Google print search, James A. Landau].
HERMITIAN FORM is found in "On Quadratic, Hermitian and Bilinear Forms" by Leonard Eugene Dickson, Transactions of the American Mathematical Society, 7 (Apr., 1906).
HERMITIAN MATRIX. C. C. MacDuffee, The Theory of Matrices, Springer (1933, p. 62) refers to C. Hermite "Remarques sur un théorème de M. Cauchy," C. R. Acad Sci., 41 (1855), p. 181. The phrase "Hermitian matrix" appears in 1866 in Arthur Cayley, "A Supplementary Memoir on the Theory of Matrices," Philosophical Transactions of the Royal Society of London Papers 4, p. 438 But this was in reference to a different matrix and to a different Hermite publication.
HESSENBERG MATRIX is found in 1954 in Neue Verfahren zur direkten Lösung des allgemeinen Matrizeneigenwertproblemes by Sigurd Falk. [Jan Peter Schäfermeyer]
The term HESSIAN was coined by James Joseph Sylvester (1814-1897), named for Ludwig Otto Hesse. Hesse introduced the concept in a paper published in 1844 and reproduced in Werke pp. 89-122.
Hessian appears in Sylvester's "Sketch of a Memoir on Elimination, Transformation, and Canonical Forms," Cambr. & Dublin Math. Jrnl., 6, 186-200, reprinted in Math. Papers J. S. S., 1:184-197: "The Hessian, or as it ought to be termed, the first Boolian Determinant" (OED).
HETERO- and HOMOSCEDASTICITY. The terms heteroscedasticity and homoscedasticity were introduced in 1905 by Karl Pearson in "On the general theory of skew correlation and non-linear regression," Drapers' Company Res. Mem. (Biometric Ser.) II. Pearson wrote, "If ... all arrays are equally scattered about their means, I shall speak of the system as a homoscedastic system, otherwise it is a heteroscedastic system." The words derive from the Greek skedastos (capable of being scattered).
Many authors prefer the spelling heteroskedasticity. J. Huston McCulloch (Econometrica 1985) discusses the linguistic aspects and decides for the k-spelling. Pearson recalled that when he set up Biometrika in 1901 Edgeworth had insisted the name be spelled with a k. By 1932 when Econometrica was founded standards had fallen or tastes had changed. See the paper "When Did We Begin to Spell 'Heteros*edasticity' Correctly?" by Alfredo R. Paloyo. [This entry was contributed by John Aldrich, referring to OED2 and David, 1995.]
HETEROLOGICAL. See AUTOLOGICAL and HETEROLOGICAL.
HEXADECIMAL. Sexadecimal appears in 1891 in the Century dictionary.
Hexadecimal is found in Carl-Erik Froeberg, Hexadecimal conversion tables, Lund: CWK Gleerup 20 S. (1952). A Google print search suggests uses in 1949 and 1950, but only snippet view is available.
In 1955, R. K. Richards used sexadecimal in Arithmetic Operations in Digital Computers: "Octonary, duodecimal, and sexadecimal are the accepted terms applying to radix eight, twelve, and sixteen, respectively" [James A. Landau].
HEXAGON. Hexagons are discussed in Book IV of Euclid's Elements. The word "hexagon" appears in English in 1570 in Sir Henry Billingsley's translation of the Elements (OED). Earlier in 1551 in Pathway to Knowledge Robert Recorde used the word siseangle: "Def., Likewyse shall you iudge of siseangles, which haue sixe corners" (OED). When writing English Recorde preferred to create new English words rather than borrow classical words. See EQUILATERAL and PENTAGON. [John Aldrich]
HEXAHEDRON. The word "hexahedron" was used by Heron to refer to a cube; he used "cube" for any right parallelepiped (Smith vol. 2, page 292).
The term HIGHER-DIMENSIONAL ALGEBRA was coined by Ronald Brown, according to an Internet web page.
The HILBERT terms recall the work of David Hilbert (1862-1943). Hilbert contributed to many branches of mathematics, including the theory of invariants (HILBERT'S FINITE BASIS THEOREM), algebraic number theory and geometry. By 1900 Hilbert's standing was such that he could pose problems for the 20th century: see HILBERT'S PROBLEMS. In the first decade of the century Hilbert made a deep study of integral equations from which his followers developed HILBERT SPACE theory. In the 1920s Hilbert became preoccupied with the foundations of mathematics: see HILBERT'S PROGRAM.
Hilbert's work inspired many mathematicians and his methods were applied to other set-ups. In 1929 J. von Neumann presented axioms for abstract Hilbert space: see p. 55 of his "Allgemeine Eigenwerttheorie Hermitescher Funktionaloperatoren" Math. Ann. 102, 49-131. In M. H. Stone's Linear Transformations in Hilbert Space (1932) "ordinary Hilbert space" is the space of square summable sequences and "abstract Hilbert space" the von Neumann space. Eventually "Hilbert space" without qualification came to mean the abstract space.
This entry was contributed by John Aldrich, based on Bernkopf and Kline chapter 46. See also EIGENVALUE.
For some non-eponymous terms with Hilbert connections, see the entries BETWEENNESS, EIGENVALUE, GENETIC METHOD, KERNEL, METAMATHEMATICS, PREDICATE CALCULUS.
HILBERT'S ANSATZ. See ANSATZ.
The HILBERT CURVE was given by Hilbert. "Über die stetige Abbildung einer Linie auf ein Flachenstück." Math. Ann. 38, 459-460, 1891. See Mathworld.
See PEANO CURVE.
HILBERT'S FINITE BASIS THEOREM. This theorem was given by David Hilbert in his "Über die Theorie der algebraischen Formen," Mathematische Annalen, 36, (1890) 473-534.
It was with reference to this theorem that Paul Gordan is supposed to have said, "This is theology, not mathematics" ("Das ist keine Mathematik, das ist Theologie!") Max Noether's obituary of Gordan in Mathematische Annalen 75, (1914) 1-41, page 18. (This topic was discussed in the Historia Matematica forum in 2001 and 1999.)
HILBERT'S HOTEL appears in English in Scientific American in 1964: "It is entertainingly illustrated by a fantasy, attributed to the noted German mathematician David Hilbert and known as 'Hilbert's Hotel.' It would be appreciated by roomless visitors to the New York World's Fair." [Google print search by James A. Landau]
HILBERT'S NULLSTELLENSATZ (theorem of the location of zeros) in algebraic geometry; see Wikipedia article. The theorem appears in Hilbert's "Über die Theorie der algebraischen Formen," Mathematische Annalen, 36, (1890) 473-534. The theorem came to be called der Hibertsche Nullstellensatz, as in J. L. Rabinowitsch "Zum Hibertschen Nullstellensatz," Mathematische Annalen, 102, (1929) 520. In English the expression became Hilbert's Nullstellensatz as in O. Zariski "A New Proof of Hilbert's Nullstellensatz," Bulletin of the American Mathematical Society, 53, (1947), 362-368. That expression, or the Hilbert Nullstellensatz, has remained the standard one in English. Contrast with the French practice of referring to "le théorème des zéros de Hilbert" or with the fate of other German expressions in English, such as das Entscheidungsproblem which became DECISION PROBLEM.
HILBERT'S PROBLEMS. In a famous address delivered in 1900 David Hilbert (1862-1943) posed 23 problems for the 20th century. Among them were the CONTINUUM HYPOTHESIS, FERMAT'S LAST THEOREM and the RIEMANN HYPOTHESIS. The problems had a great influence on the development of mathematics in the 20th century but the phrase "Hilbert's problems" seems to have become automatic only relatively recently: a JSTOR search found it in 1950 in the American Mathematical Monthly, the "so-called 'Hilbert problems'". The term seems to appear in 1944 in the Bulletin of the American Mathematical Society, based on a snippet view from a Google print search by James A. Landau.
HILBERT'S PROGRAM, named for David Hilbert (1862-1943), refers to the program in the foundations of mathematics he formulated in the 1920s. According to Richard Zach's Hilbert's program, the program "calls for a formalization of all of mathematics in axiomatic form, together with a proof that this axiomatization of mathematics is consistent."
An address by Eliakim Hastings Moore in Science, March 13, 1903, has:
One has then the feeling that the carrying out in an absolute sense of the program of the abstract mathematicians will be found impossible. At the same time, one recognizes the importance attaching to the effort to do precisely this thing. The requirement of rigor tends toward essential simplicity of procedure, as Hilbert has insisted in his Paris address, and the remark applies to this question of mathematical logic and its abstract expression.[Google print search, James A. Landau]
It appears from a Google print search with snippet view that in 1930 On the Logic of Measurement by Ernest Nagel has:
Consequently, it is Hilbert's program to reduce the whole of mathematics to a formal, meaningless play with marks, so that the pursuit of mathematics becomes a glorified game of chess. The rules of the game, designated as "metamathematics," have a meaning, but only in the terms of the meaningless operations with signs to which "mathematics" has been. . . .A JSTOR search found Hilbert program in 1934 in Alonzo Church's "The Richard Paradox," American Mathematical Monthly, 41, p. 360.
HILBERT'S SATZ 90. The theorem is the 90th in David Hilbert's Die Theorie der algebraischen Zahlkörper, the famous Zahlbericht of 1897: p. 149 in Hilbert's Gesammelte Abhandlungen Erster Band. See the Wikipedia entry.
HILBERT SPACE is named after David Hilbert (1862-1943) but it was not introduced by him in the sense that BANACH SPACE was introduced by Banach. Hilbert did not give a set of postulates and indeed he "never refers explicitly to 'spaces' or 'function spaces' in any of his work. [His] chief aim is to get on with the job of solving analytic problems" wrote M. Bernkopf (p. 10) in "The Development of Function Spaces with Particular Reference to their Origins in Integral Equation Theory" Arch. Hist. Exact Sci. 3, (1966), 1-96.
Hilbert treated square summable sequences in the fourth of his communications on integral ("Grundzüge einer allgemeinen Theorie der linearen Integralgleichungen. Vierte Mitteilung" Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen, Mathematisch-Physikalische Klasse (1906), pp. 157-227. His student Erhard Schmidt gave the treatment a geometric interpretation in his "Über die Auflösung linearer Gleichungen mit unendlich vielen Unbekannten," Rendiconti di Matematico di Palermo, 25, (1908), 53-77. The expression "the Hilbert space" was used first for this (l2) set-up. See e.g. E. R. Hedrick "On Properties of a Domain for Which Any Derived Set is Closed." Transactions of the American Mathematical Society, 12, (1911), 285-294 (JSTOR search).
HINDU-ARABIC NUMERAL. According to Katz, the earliest available arithmetic text to deal with Hindu numbers is the Arabic work Book on Addition and Subtraction after the Method of the Indians by Muhammad ibn Musa al-Khwarizmi. This system of notation was introduced into Europe by Fibonacci.
In his Liber abaci (1202) Fibonacci referred to Indian figures:
Novem figure indorum he sunt 9 8 7 6 5 4 3 2 1.For some time the Hindu origins of the notation were forgotten so that the term Arabic characters appears in Chambers Cyclopedia: "The Arabic characters stand contradistinguished to the Roman" (1727-51). Arabic numerals appears in in T. Green, Extracts from the diary of a lover of literature: "Writing, he deduces, from pictural representations, through hieroglyphics ... to arbitrary marks ... like the Chinese characters and Arabic numerals." (1810).
[The nine Indian figures are 9 8 7 6 5 4 3 2 1.]
The 1872 edition of Chambers Encyclopaedia uses the term Hindu numerals: "After the introduction of the decimal system and the Arabic or Hindu numerals about the 11th c., Arithmetic began to assume a new form." The term Indo-Arabic system appears in the 1884 edition of the Encyclopaedia Britannica: "In Europe, before the introduction of the algorithm or full Indo-Arabic system with the zero."
The historians of mathematics wanted to set the record straight. In A History of Mathematics Florian Cajori wrote:
Generally we speak of our notation as the 'Arabic' notation, but it should be called the 'Hindoo' notation, for the Arabs borrowed it from the Hindoos. ... These Singhalesian signs, like the old Hindoo numerals, are supposed originally to have been the initial letters of the corresponding numerical adjectives.(This is from the 1906 edition but presumably the passage appears in the earlier 1893 edition).
David Eugene Smith and Louis Charles Karpinski called their book (1911) The Hindu-Arabic Numerals.
For more information see the MacTutor articles Indian numerals and Arabic numerals.
HISTOGRAM. The term histogram was coined by Karl Pearson. In his Contributions to the Mathematical Theory of Evolution. II. Skew Variation in Homogeneous Material, Philosophical Transactions of the Royal Society A, 186, (1895) Pearson explained in a footnote (p. 399) that the term was "introduced by the writer in his lectures on statistics as a term for a common form of graphical representation, i.e., by columns marking as areas the frequency corresponding to the range of their base."
The term histogram appears in a lecture of November 1891 in the series of lectures on the "Geometry of Statistics" that Pearson gave at Gresham College in the academic year 1891-2. The lectures are described by S. M. Stigler History of Statistics pp. 326-7 and T. M. Porter Karl Pearson: The Scientific Life in a Statistical Age, p. 236.
Pekka Pere contributed to this entry. See the entry RADIOGRAM.
HöLDER MEAN and HöLDER'S INEQUALITY both derive from Otto Hölder 1889 paper "Über ein Mittelwertsatz," Nachrichten von der Königl. Gesellschaft der Wissenschaften und der Georg-Augusts-Universität zu Göttingen, 38-47.
Hölder's means and Hölder's inequality are found in English in 1901 in The Theory of Functions of a Real Variable and the Theory of Fourier's Series by E. W. Hobson. [Google print search by James A. Landau]
Hölder mean has also been used to refer to a construction in the theory of divergent series. This concept comes from Hölder's "Grenzwerthe von Reihen an der Convergenzgrenze," Mathematische Annalen, 20, (1882), 535-49.
HOLDER SUMMABILITY (written as Hölder-summability) is found in English in April 1913 in "On the Definition of the Sum of a Divergent Series" by Louis Lazarus Silverman in The University of Missouri Studies Mathematics Series. [Google print search by James A. Landau]
The terms HOLOMORPHIC FUNCTION and MEROMORPHIC FUNCTION were introduced by Charles A. A. Briot (1817-1882) and Jean-Claude Bouquet (1819-1885) in their Théorie des fonctions elliptiques (1859). According to the OED and to Schwartzman, mero- comes from the Hellenistic Greek μερο and signifies 'part' or 'partial' while holo- is based on the Greek
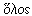 and signifies 'whole.'
and signifies 'whole.'
A Google print search finds holomorphic in English in "Solution of the Equation of the Fifth Degree," The Analyst, Nov. 1878. The article is a translation of the above work by Briot and Bouquet. [James A. Landau]
A Google print search finds meromorphic in English in 1885 in "Extrait d'une letter de M. Hermite," American Journal of Mathematics: "the function f(z)/z(n-1) being meromorphic over the whole sphere must be a rational fraction...." [James A. Landau]
Cauchy had used the terms monotypique, monodrome, monogen, and synetique in his articles of 1851 Comptes rendus, 32 pp. 68-75 and 162-4. (Kline, p. 642).
HOMEOMORPHISM. The terms homéomorphisme and homéomorphe appear in J. H. Poincaré's "Analysis Situs," Journal de l'école Polytechnique, 1, (1892) 1-121:
nous dirons que les deux variétés V et V' sont equivalents au point de vue de l' Analysis situs, ou pour abrégrer le langage, qu'elles sont homéomorphes, c'est-à-dire de forme pareille.Homeomorphism and homeomorphic are found in English in American Mathematical Society Colloquium Lectures, Volume V Cambridge Colloquium 1916. The publication date is given as 1918. "A (1-1) continuous transformation of a complex into itself or another complex is called, following Poincaré, a homeomorphism. Two complexes related by a homeomorphism are said to be homeomorphic." [Google print search by James A. Landau]
As G. H. Moore points out in his "The evolution of the concept of homeomorphism," Historia Mathematica, 34, (2007), 333-343, Poincaré meant by homeomorphism "something quite different from and more restricted than" what is meant by the term today: in particular, Poincaré's notion of homeomorphism had strong requirement of differentiability and smoothness that "have nothing directly to do with topology." Moore identifies a string of contributors to the modern notion of homeomorphism which was established around 1930. The modern notion is found in Lefschetz Topology (1930), Kuratowski Topologie I (1933) and Alexandroff & Hopf Topologie (1935).
This entry was contributed by John Aldrich. See also the entry TOPOLOGY.
HOMOGENEITY is found in English in 1736 in The Method of Fluxions and Infinite Series: with its application to the theory of curve lines by Isaac Newton: "As Velocities can be compared only with Velocities, and all other quantities with others of the same Species only; therefore in every Term of an Equation, the Fluxions must always ascend to the same number of Dimensions, that the homogeneity may not be destroy'd." [Google print search by James A. Landau]
HOMOGENEOUS is found in 1795 in A Mathematical and Philosophical Dictionary Vol. II by Charles Hutton, under "Addenda and Corrigenda" on page 722: "Somewhat concerning the reduction of some fluxional equations to homogeneous, and concerning homogeneous equations of different orders; and of reducing an homogenous fluxional equation of order to a fluxional equation of n - 1 order ...." [Google print search by James A. Landau]
HOMOGENEOUS DIFFERENTIAL EQUATION is found in 1868 in A Treatise on the Differential and Integral Calculus: And on the Calculus of Variations by Edward Henry Courtenay: "Prop. To determine the factor necessary to render a homogenous differential equation exact." [Google print search]
The term HOMOGRAPHIC is due to Michel Chasles (1793-1880) (Smith, 1906).
Homographic is found in 1859 in "A Sixth Memoir upon Quantics" by Arthur Cayley, Philosophic Transactions of the Royal Society of London for the year MDCCCLIX. [Google print search by James A. Landau]
HOMOLOGOUS. Writing in Latin, Cavalieri used homologe in 1643 in Geometria indivisibilibus continuorum: noua quadam ratione promota. [Google print search, James A. Landau]
Homologous is found in English in 1656 in The History of Philosophy, in Eight Parts by Thomas Stanley: "Of equiangle triangles, the sides that are about equall angles are proportionall, and the sides that subtend the equall angles are homolgous." [Google print search, James A. Landau]
Homologous is found in Arthur Cayley, "On the Triple Tangent Planes of Surfaces of the Third Order," The Cambridge and Dublin Mathematical Journal, vol. IV (1849), pp. 118-132: "Considering two lines in the same triple tangent plane, the remaining triple tangent planes through these two lines respectively are homologous systems." [James A. Landau]
HOMOLOGY is found in 1749 in James Stirling, The Differential Method, or a Treatise Concerning Summation and Interpolation of Infinite Series, Translated into English, with the Author's Approbation, by Francis Holliday: "Consequently by gathering the homologous terms into one, the series will be reduced to its first form, and will be ομολογια, homology, or likeness, of the terms no where depends on the co-efficients A, B, C, D, &c. but altogether upon the indeterminate quantity z ...." [Google print search, James A. Landau]
Homology is found in Arthur Cayley, "Sur le Problème des Contacts," Journal für die reine and angewandte Mathematik (Crelle), tom. XXXIX (1850), pp. 4-13:
...nous dirons que les deux côtés du quadrangle inscrit qui se coupent dans le point d'intersection des deux chordes de contact, sont les axes de symptose des deux coniques données, et que les deux angles du quadrilatère circonscrit, situés sur la droite qui passe par les deux centres de contact, sont les centres d'homologie des deux coniques données. Soient maintenant inscrites trois coniques à la même conique. En combinant deux à deux ces trois coniques, les six axes de symptose se couperont trois à trois en quatre points que nous nommerons centres de symptose, et les six centres d'homologie seront situés trois à trois sur quatre droites que nous appelerons axes d'homologie.[James A. Landau]
...ces equations ... correspondent à un centre d'homologie des deux coniques ... on obtient facilement, pour un des axes d'homologie des trois coniques ... et celles des trois autres axes d'homologie ...
Cherchons le pôle de l'axe d'homologie dont nous venons de trouver l'équation
Homology is found in English in 1879 in Conic Sections by George Salmon: "Two triangles are said to be homologous, when the intersections of the corresponding sides lie on the same right line called the axis of homology; prove that the lines joining corresponding vertices meet in a point" [OED].
Homology is found in a more modern usage, originally in algebraic topology but now more widespread (as in homological algebra) in 1895 in H. Poincaré, Analysis situs [Joseph Rotman].
HOMOMORPHISM and homomorphic are found in 1921 in Primitive Groups Part I by William Albert Manning. [Google print search by James A. Landau]
HOMOTOPY. The OED refers to O. Veblen Analysis Situs (1922) (Cambridge Colloq. Lect., Vol. 5, Pt. 2) v. 126 "The term homotopy will be used to designate a deformation in the general sense..and two generalized complexes..will be said to be homotopic if one can be carried into the other by means of a homotopy."
According to Lefschetz Topology (1930, p. 77), the term was introduced in Dehn & Heegaard's Analysis situs in the Encyklopädie der mathematischen Wissenschaften (1907, pp. 153ff.)
HORNER'S METHOD. "Mr. Horner's new method of solving numerical equations of all orders, by continuous approximations" appears in "A New Method of Solving Numerical Equations of All Orders, By Continuous Approximation," by W. G. Horner, Esq. Communicated by Davies Gilbert, Esq. F.R.S. Read July 1, 1819, Philosophical Transactions of the Royal Society of London for the year MDCCCXIX. [Google print search, James A. Landau]
Theophilus Holdred wrote in a letter, "The method I have given at the end of my Supplement, Mr. Nicholson calls Mr. Horner's method; and says I have been anticipated by himself in point of publication: but it resembles Mr. Horner's in no respect...." The letter appears in The Philosophical Magazine and Journal Volume LVI For July, August, September, October, November, and December, 1820.
Horner's method appears in 1842 in the Penny Cyclopedia: "The use of Horner's method is very much more easy than that of Newton" [OED].
HOUSEHOLDER TRANSFORMATION. This matrix was used by Alston S. Householder in his "Unitary Triangularization of a Nonsymmetric Matrix," Journal of the ACM (JACM), 5, Issue 4 (October 1958), 339 – 342. Householder did not give the matrix a name but in The Theory of Matrices in Numerical Analysis (1964, p. 4) he calls it an "elementary Hermitian matrix." The term "elementary reflector" is also used. A JSTOR search found the term Householder transformation in use by the mid-1960s. [John Aldrich]
HYPERBOLA was probably coined by Apollonius, who, according to Pappus, had terms for all three conic sections.
However, G. J. Toomer believes the names parabola and hyperbola are older than Apollonius, based on an Arabic translation of Diocles' On burning mirrors.
Hyperbola was used in English in 1668 by Barrow in correspondence: "The rules I sent you concerning the hyperbola, I cannot well exemplify."
Hyperbola also appears in English in 1668 in the Philosophical Transactions of the Royal Society [OED].
The term HYPERBOLIC FUNCTION was introduced by Lambert in 1768 [Ken Pledger].
The terms HYPERBOLIC GEOMETRY, ELLIPTIC GEOMETRY, and PARABOLIC GEOMETRY were introduced by Felix Klein (1849-1925) in 1871 in "über die sogenannte Nicht-Euklidische Geometrie" (On so-called non-Euclidean geometry), reprinted in his Gesammelte mathematische Abhandlungen I (1921) p. 246. The page can be viewed here (Ken Pledger and Smart, p. 301).
HYPERBOLIC LOGARITHM. Because of the relation between natural logarithms and the areas of hyperbolic sectors, natural logarithms came to be called hyperbolic logarithms. The connection between natural logarithms and sectors was discovered by Gregory St. Vincent (1584-1667) in 1647, according to Daniel A. Murray in Differential and Integral Calculus (1908).
Hyperbolic logarithm is found in 1717 in Geometry Improv'd by A. S. Philomath (Abraham Sharp). [Google print search by James A. Landau]
HYPERBOLIC PARABOLOID appears in 1836 in the second edition of Elements of the Differential Calculus by John Radford Young [James A. Landau].
HYPERBOLIC SINE and HYPERBOLIC COSINE. Vincenzo Riccati (1707-1775) introduced hyperbolic functions in volume I of his Opuscula ad Res Physicas et Mathematicas pertinentia of 1757. Presumably he used these terms, since he used the notation Sh x and Ch x.
Hyperbolic sine and hyperbolic cosine are found in English in "Report of the Third Meeting of the British Association for the Advancement of Science, Held at Cambridge in 1833." [Google print search, James A. Landau]
HYPERCOMPLEX is dated ca. 1889 in MWCD10.
HYPERCUBE is found in Joseph Delboeuf, "L'ancienne et les nouvelles géométries. II," Revue Philosophique de la France et de l'étranger 37 (1894), 353-383 [Google print search].
Hyper-cube is found in English in April 1894 in St. Nicholas: An Illustrated Magazine for Young Folks: "When we wish to represent the fourth power (which being of four dimensions we may call a hyper-cube), we may do so in solid perspective by placing a cube diagonally above another, and a little behind it, and joining the corresponding corners." [Google print search by James A. Landau]
HYPERDETERMINANT was Cayley's term for independent invariants (DSB). He coined the term around 1845.
According to Eric Weisstein's Internet web page, "Cayley (1845) originally coined the term, but subsequently used it to refer to an Algebraic Invariant of a multilinear form."
Hyperdeterminant was used by Cayley in 1845 in Camb. Math. Jrnl. IV. 195: "The function u whose properties we proceed to investigate may be conveniently named a 'Hyperdeterminant'" [OED].
Hyperdeterminant was used by Cayley about 1846 in Camb. & Dublin Math. Jrnl. I. 104: "The question may be proposed 'To find all the derivatives of any number of functions, which have the property of preserving their form unaltered after any linear transformations of the variables'... I give the name of Hyperdeterminant Derivative, or simply of Hyperdeterminant, to those derivatives which have the property just enunciated" [OED].
The term HYPERELLIPTICAL FUNCTION (ultra-elliptiques) was coined by Legendre, according to an article by Jacobi in Crelle's Journal in which Jacobi went on to propose instead the term Abelian transcendental function (Abelsche Transcendenten) (DSB).
The term HYPERGEOMETRIC (to describe a particular differential equation) is due to Johann Friedrich Pfaff (1765-1825) (Kline, page 489).
The term HYPERGEOMETRIC CURVE is found in the title "De curva hypergeometrica hac aequatione expressa y=1*2*3*...*x" by Leonhard Euler. The paper was presented in 1768 and published in 1769 in Novi Commentarii academiae scientiarum Petropolitanae.
HYPERGEOMETRIC DISTRIBUTION appears in the title of H. T. Gonin, "The use of factorial moments in the treatment of the hypergeometric distribution and in tests for regression," Philosophical Magazine, 7, Ser. 21, 215-226 (1936).
The name is relatively recent but the distribution first appears as the solution to Problem IV of Huygens's De Ratiociniis in Ludo Aleae (1657, p.
12). Several people, besides Huygens, solved the problem and James Bernoulli and de Moivre gave solutions for the general case. See Hald (1990, pp. 201-2). At the end of the 19th century Karl Pearson wrote a paper in which he considered fitting the distribution (given by the "hypergeometrical series") to data: "On Certain Properties of the Hypergeometrical Series, and on the Fitting of such Series to Observation Polygons in the Theory of Chance," Philosophical Magazine, 47, (1899), 236-246. [John Aldrich]
HYPERGEOMETRIC SERIES. According to Geschichte der Elementar-Mathematik by Karl Fink, Wallis and Euler used this term for the series in which the quotient of any term divided by the preceding is an integral linear function of the index, and J. F. Pfaff proposed the term for the general series in which the quotient of any term divided by the preceding is a function of the index.
The 1816 translation of Lacroix's Differential and Integral Calculus has: "These series, in which the number of factors increases from term to term, have been designated by Euler ... hypergeometrical series" [OED].
HYPERSET is found in 1987 in The Liar: An Essay on Truth and Circularity by John Barwise and John Etchemendy: "the sets we get on Aczl's conception include all those in the traditional, wellfounded universe. But in addition to these, we get a rich class of nonwellfounded sets, or as we will sometimes call them, hypersets." [Google print search, James A. Landau]
Hyperset is also found in 1991 in the article "Hypersets," by Barwise and Larry Moss in Mathematical Intelligencer.
HYPERSPHERE. Ludwig Schläfli, On the multiple integral ∫n dx dy ... dz, whose limits are p1 = a1x + b1y + ... + h1z > 0, p2 > 0, ... pn > 0, and x2 + y2 + ... + z2 < 1, Quarterly Journal of Pure and Applied Mathematics 2 (1858), 269-301 has on p. 280:
We do not dwell further on this general subject, but we proceed to one of its most particular cases, the general spheric equation ; the origin here assumed may be called centre and the constant a radius. For the curved continuum itself, represented by this equation, I propose the term polysphere or n-sphere; thus, a pair of points in a straight line will be a monosphere, the circle a disphere, and the spherical surface properly so called a trisphere. These terms are very harsh, but I do not know how to avoid this.George Salmon, On the relation which connects the mutual distances of five points in space, Quarterly Journal of Pure and Applied Mathematics 3 (1860), 282-288, has on p. 285:
It must have occurred to any person who has observed the analogy between the processes of the analytic geometry of three and of two dimensions, that as far as algebraic processes are concerned there is nothing to limit the methods employed to the case of three dimensions. If, for example, there were any beings who could conceive space of four dimensions, we could with our present faculties write as good a book of analytic geometry for their use as if we could conceive space of four dimensions ourselves. We should take four hyper-planes at right angle to each other, and define the position of any point by four coordinates expressing its four distances from these; and so proceed in every manner exactly as we proceed in the analytic geometry of three dimensions. [...] Now the process followed in Art. (2) may be extended word for word to space of four dimensions and gives the following relation between the distances of five points on a hyper-sphere.[This entry was contributed by Dave L. Renfro.]
HYPOTENUSE was used by Pythagoras (c. 540 BC).
It is found in English in 1571 in A geometrical practise named Pantometria by Thomas Digges (1546?-1595): "Ye squares of the two contayning sides ioyned together, are equall to the square of ye Hypothenusa" [OED].
In English, the word has also been spelled hypothenusa, hypotenusa, and hypothenuse.
HYPOTHESIS and HYPOTHESIS TESTING in Statistics. Although the use of probability in testing hypotheses is almost as old as the study of probability, the modern terminology was largely created by R. A. Fisher and the team of J. Neyman and E. S. Pearson in the 1920s and -30s. These parties disagreed about the theory of testing but their terminologies are blended in modern Statistics. (For the earliest test see the entry SIGNIFICANCE.)
Hypothesis and test only became standard terms in the 1920s: they were not used in such classics as Karl Pearson (1900) on goodness of fit or Student (1908) on tests on the normal mean. The term was very prominent in R. A. Fisher's Statistical Methods for Research Workers (1925). See the entries on CHI-SQUARE, P-VALUE and STUDENT's t-DISTRIBUTION
Fisher's favoured term was test of significance while test of hypothesis is found in 1928 in J. Neyman and E. S. Pearson, "On the use and Interpretation of Certain Test Criteria for Purposes of Statistical Inference. Part I," Biometrika, 20 A, 175-240. (This paper introduced the likelihood ratio test.) See the entries on SIGNIFICANCE and LIKELIHOOD RATIO.
Neyman and Pearson (1928) speak of accepting and rejecting hypotheses. Fisher had not used the term rejecting but he had no objection to it. However he did object to accepting (see below).
Alternative hypothesis is used several times in the 1928 paper but it was canonised in Neyman and Pearson's most important paper, "On the Problem of the Most Efficient Tests of Statistical Hypotheses," Philosophical Transactions of the Royal Society of London. Series A, 231. (1933), pp. 289-337. The role they gave to the alternative hypothesis also drew criticism from Fisher. See POWER.
The 1933 paper introduced the terms simple hypothesis and composite hypothesis. The paper contained many other new terms and new results. See the entries on CRITICAL REGION, NEYMAN-PEARSON LEMMA, SAMPLE SPACE, SIMILAR REGION, SIZE, TYPE I ERROR
Null hypothesis appears in 1935 in Fisher's The Design of Experiments. He writes, "[W]e may speak of this hypothesis as the 'null hypothesis,' and it should be noted that the null hypothesis is never proved or established, but is possibly disproved, in the course of experimentation." (p. 19)
The "null hypothesis" is often identified with the "hypothesis tested" of the Neyman-Pearson 1933 paper and represented by their symbol H0. Neyman did not like the term "null hypothesis," arguing (First Course in Probability and Statistics, 1950, p. 259) that "the original term 'hypothesis tested' seems more descriptive." It is not clear, however, that "hypothesis tested" was ever floated as a technical term.
This entry was contributed by John Aldrich. See also ASYMPTOTIC RELATIVE EFFICIENCY, CHI-SQUARE, CRITICAL REGION, NEYMAN-PEARSON (FUNDAMENTAL) LEMMA, NUISANCE PARAMETER, P-VALUE, POWER, SIGNIFICANCE, SIMILAR REGION, SIZE, TYPE I ERROR, STUDENT's t-DISTRIBUTION.